上海市重点中学2010届高三数学月考试题（理科）

已知:intx=1,y=2,z;则执行z=xy?＋＋x:＋＋y;则z的值为()。

A.1

B.2

C.3

D.4


正确答案:C

所示为一手摇提升装置,其中各轮的齿数为:z1=20,z2=50,z2′=15,z3=45,z3′=1,z4=40,z4′=17,z5=51。 (1)试在图上标出提升重物时手柄及各个轮的转向; (2)试求传动比i15。


参考答案：

已知“int w=1,x=2,y=3,z=4;”,则表达式“w>x?w:z>y?z:x”的值是()

A.1

B.2

C.3

D.4


正确答案：D

已知w=3,x=2,y=3,z=3,a=4,b=2;则执行语句(a=w>x)||(b=y>z);后,a,b的值为(C)。

A.1和1

B.0和0

C.1和2

D.4和2


正确答案：C

过点(4，-1，3)且平行于直线L：(x-3)/2=y=(z-1)/5的直线方程为( ).

A.(x-4)/2=(y+1)/0=(z-3)/5
B.(x-4)/2=(y+1)/1=(z-3)/5
C.(x+4)/2=(y-1)/0=(z+3)/5
D.(x+4)/2=(y-1)/1=(z+3)/5

答案：B
解析：

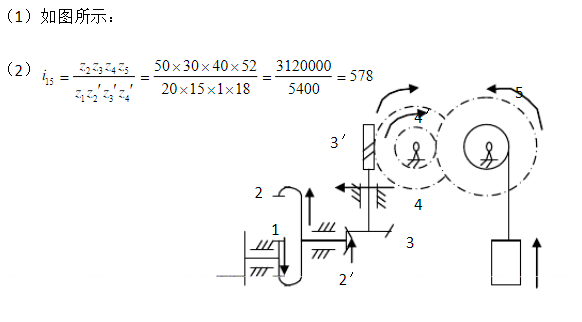
1上海市重点中学 2010 届高三数学月考试题（理科）、填空题：（4 分 14=56 分）5合 037 3,512是实数，则 z 3则 k Z 1)(1 )(1|)是：（1）偶函数 （2）周期函数，（3）定义域为 2, （4）值域为0，1，其中正确的是_（1） （4）7. 将棱长为 3 的正四面体的各条棱三等分,经过分点将原正四面体各顶点附近均截去一个棱长为1 的小正四面体,则剩下的多面体的棱数是_进三分球的个数分别为a,321，则右图表示的框图输出的 s 的实际意义是 是双曲线214的左焦点， (1,4) 最小值为 C、圆 2:4足为(1,2)M，则四边形 面积的最大值为 当无理数 x= 时，代数式 3122有标号分别为 ， ， 的三张卡片，现从这个盒子中，有放回地先后抽得两张卡片的标号分别为 、 y，记 则随机变量 的数学期望是_ 942: 132A(作斜率为 )0的两条直线，分别交椭圆于点，则直线 的斜率为_ 2)(（ ),2） ，若存在闭区间 ,使得对任意 有 (xf=c（ 为实常数） ，则实数 值依次为 1和 1二、选择题：（本大题共 4 题，每题 5 分，共 20 分）、3、4、5、6（单位： 5 根细木棒围成一个三角形（允许连接，但不允许折断） ，能够得到的三角形的最大面积为（ B ）A 28 B 210c C 23 D l的大小为 06， 过点 和平面 所成的角都是 03的直线的条数为（ ） B2 C3 D417已知 0)(x)f b，且方程 (无实根。现有四个命题：方程f也一定无实根；若 ，则不等式 的一切 立；若 0a，则必存在实数 0)(若 0不等式 (对一切立。其中真命题的个数是（ ） B. 2 个 C. 3 个 D. 4 是 内心，则下列等式恒成立的是( )D(A) 0 (B) 0(C) 02 (D) . 3三、解答题 （14+14+14+14+18=74 分）19. 如图，圆锥的顶点为 S，底面中心为 O与底面直径 直的一条半径，D 是母线 中点 （1）求证： 可能垂直；（2 ）若圆锥的高为 4，异面直线 成角的大小为 2圆锥的体积证法一：反证法。若 又 以 面 已知 ，所以 /，矛盾所以 与 可能垂直证法二：建立如图坐标系，设圆锥的高为 h，底面半径为 r，则 (0,)(,0)(,)0,)(0,),(,0) 2所以 A 不垂直（2 ） 建立如图坐标系，设底面半径为 ，由高为 4则 ),(r、 (,2)D，则(,)， (,0) ， 2221654，由 成角为 2以 2615r，所以 233)(2)若函数 )(4,，求实数 ）若函数)(，都有 ,，求实数 的值；（） 已知,13a，求函数 )(1） 4；（2） 4,（3） ,5921. 某大型超市在

设平面π的方程为3x －4y －5z －2 = 0，以下选项中错误的是：
(A)平面π过点（－1，0，－1）
(B)平面π的法向量为－3i + 4 j + 5k


(D) 平面π与平面－2 x －y －2 z + 2 = 0垂直


答案：D
解析：

过点(4，-1，3)且平行于直线L：(x-3)/2=y=(z-1)/5的直线方程为( ).

A.(x-4)/2=(y+1)/0=(z-3)/5
B.(x-4)/2=(y+1)/1=(z-3)/5
C.(x+4)/2=(y-1)/0=(z+3)/5
D.(x+4)/2=(y-1)/1=(z+3)/5

答案：B
解析：

过点(4，-1，3)且平行于直线L：(x-3)/2=y=(z-1)/5的直线方程为( ).

A.(x-4)/2=(y+1)/0=(z-3)/5
B.(x-4)/2=(y+1)/1=(z-3)/5
C.(x+4)/2=(y-1)/0=(z+3)/5
D.(x+4)/2=(y-1)/1=(z+3)/5

答案：B
解析：

过点(4，-1，3)且平行于直线L：(x-3)/2=y=(z-1)/5的直线方程为( ).

A.(x-4)/2=(y+1)/0=(z-3)/5
B.(x-4)/2=(y+1)/1=(z-3)/5
C.(x+4)/2=(y-1)/0=(z+3)/5
D.(x+4)/2=(y-1)/1=(z+3)/5

答案：B
解析：

过点(4，-1，3)且平行于直线L：(x-3)/2=y=(z-1)/5的直线方程为( ).

A.(x-4)/2=(y+1)/0=(z-3)/5
B.(x-4)/2=(y+1)/1=(z-3)/5
C.(x+4)/2=(y-1)/0=(z+3)/5
D.(x+4)/2=(y-1)/1=(z+3)/5

答案：B
解析：

更多 “上海市重点中学2010届高三数学月考试题（理科）” 相关考题
考题 填空题设f（x，y，z）＝exyz2，其中z＝z（x，y）是由x＋y＋z＋xyz＝0确定的隐函数，则fx′（0，1，－1）＝____。正确答案：1解析：构造函数F（x，y，z）＝x＋y＋z＋xyz，则有∂z/∂x＝－Fx′/Fz′＝－（1＋yz）/（1＋xy），（∂z/∂x）|（0，1，－1）＝0，又由f（x，y，z）＝exyz2 ，得fx′＝exyz2＋exy·2z·zx′，代入（0，1，－1），得fx′（0，1，－1）＝e0×1×（－1）2＋e0×1×2×（－1）×0＝1。
查看答案
考题 填空题设f（x，y，z）＝exyz2，其中z＝z（x，y）是由x＋y＋z＋xyz＝0确定的隐函数，则fx′（0，1，－1）＝____。正确答案：1解析：构造函数F（x，y，z）＝x＋y＋z＋xyz，则有∂z/∂x＝－Fx′/Fz′＝－（1＋yz）/（1＋xy），（∂z/∂x）|（0，1，－1）＝0，又由f（x，y，z）＝exyz2 ，得fx′＝exyz2＋exy·2z·zx′，代入（0，1，－1），得fx′（0，1，－1）＝e0×1×（－1）2＋e0×1×2×（－1）×0＝1。
查看答案
考题 填空题设f（x，y，z）＝exyz2，其中z＝z（x，y）是由x＋y＋z＋xyz＝0确定的隐函数，则fx′（0，1，－1）＝____。正确答案：1解析：构造函数F（x，y，z）＝x＋y＋z＋xyz，则有∂z/∂x＝－Fx′/Fz′＝－（1＋yz）/（1＋xy），（∂z/∂x）|（0，1，－1）＝0，又由f（x，y，z）＝exyz2 ，得fx′＝exyz2＋exy·2z·zx′，代入（0，1，－1），得fx′（0，1，－1）＝e0×1×（－1）2＋e0×1×2×（－1）×0＝1。
查看答案
考题 单选题Which of the following choices could be equal to set Z ifX = {2, 5, 6, 7, 9} and Y = {2, 5, 7}X ∪ Y ∪ Z = {1, 2, 3, 4, 5, 6, 7, 8, 9}X ∩ Z = {2, 6}Y ∩ Z = {2}A Z= {1, 4, 8}B Z= {1, 3, 8}C Z= {1, 3, 4, 8}D Z= {1, 2, 3, 4, 6, 8}E Z= {1, 2, 3, 5, 6, 8}正确答案：B解析：We know that: X = {2, 5, 6, 7, 9} and Y = {2, 5, 7}, X ∪ Y ∪ Z = {1, 2, 3, 4, 5, 6, 7, 8, 9}. This tells us that Z must contain {1, 3, 4, 8} because these elements are in the union of X, Y, and Z but not in set X and not in set Y.We also know that: X ∩ Z = {2, 6}, Y ∩ Z = {2}. This tells us that Z must also contain {2, 6}. Only choice D contains all these elements. Z = {1, 2, 3, 4, 6, 8}
查看答案
考题 过点（4，-1，3）且平行于直线L：（x-3）/2=y=（z-1）/5的直线方程为（）.A、（x-4）/2=（y+1）/0=（z-3）/5B、（x-4）/2=（y+1）/1=（z-3）/5C、（x+4）/2=（y-1）/0=（z+3）/5D、（x+4）/2=（y-1）/1=（z+3）/5正确答案:B
查看答案
考题 填空题交流电桥各桥臂的复阻抗分别为Z1，Z2，Z3，Z4，各阻抗的相位角分别为ϕ1ϕ2ϕ3ϕ4，若电桥平衡条件为Z1/Z4=Z2/Z3，那么相位平衡条件应为（）。正确答案：φ1+φ3=φ2+φ4解析：暂无解析
查看答案
考题 填空题设f（x，y，z）＝exyz2，其中z＝z（x，y）是由x＋y＋z＋xyz＝0确定的隐函数，则fx′（0，1，－1）＝____。正确答案：1解析：构造函数F（x，y，z）＝x＋y＋z＋xyz，则有∂z/∂x＝－Fx′/Fz′＝－（1＋yz）/（1＋xy），（∂z/∂x）|（0，1，－1）＝0，又由f（x，y，z）＝exyz2 ，得fx′＝exyz2＋exy·2z·zx′，代入（0，1，－1），得fx′（0，1，－1）＝e0×1×（－1）2＋e0×1×2×（－1）×0＝1。
查看答案
考题 过点(4，-1，3)且平行于直线L：(x-3)/2=y=(z-1)/5的直线方程为( ).A.(x-4)/2=(y+1)/0=(z-3)/5 B.(x-4)/2=(y+1)/1=(z-3)/5 C.(x+4)/2=(y-1)/0=(z+3)/5 D.(x+4)/2=(y-1)/1=(z+3)/5答案：B解析：
查看答案
考题 填空题交流电桥各桥臂的复阻抗分别为Z1，Z2，Z3，Z4，各阻抗的相位角分别为ϕ1ϕ2ϕ3ϕ4，若电桥平衡条件为Z1/Z4=Z2/Z3，那么相位平衡条件应为（）。正确答案：φ1+φ3=φ2+φ4解析：暂无解析
查看答案
考题 单选题过点（4，-1，3）且平行于直线L：（x-3）/2=y=（z-1）/5的直线方程为（）.A （x-4）/2=（y+1）/0=（z-3）/5B （x-4）/2=（y+1）/1=（z-3）/5C （x+4）/2=（y-1）/0=（z+3）/5D （x+4）/2=（y-1）/1=（z+3）/5正确答案：A解析：暂无解析
查看答案
相关内容
最新试卷
热门试卷