填空题设f（x，y，z）＝exyz2，其中z＝z（x，y）是由x＋y＋z＋xyz＝0确定的隐函数，则fx′（0，1，－1）＝____。

题目
填空题
设f（x，y，z）＝exyz2，其中z＝z（x，y）是由x＋y＋z＋xyz＝0确定的隐函数，则fx′（0，1，－1）＝____。
相似考题

1.(本题满分7分)设函数z=z(x，y)由方程x2+y2+z2=xyz确定，求δz/δy。

2.一平面通过两点M1(1，1，1)，M2(0，1，-1)，且垂直于平面x+y+z=0，则它的方程为( )。 A.2x+y-z=0 B.2x-y+z=0 C.x-y-z=0 D.2x-y-z=O

3.A.只能确定一个具有连续偏导数的隐函数z=z（x，y） B.可确定两个具有连续偏导数的隐函数y=y（x，y）和z=z（x，y） C.可确定两个具有连续偏导数的隐函数x=x（x，y）和z=z（x，y） D.可确定两个具有连续偏导数的隐函数x=x（y，z）和y=y（x，z）

4.(本题满分8分) 设函数z=z(x，y)是由方程x+y3+z+e2x=1所确定的隐函数，求dz．

更多“设f（x，y，z）＝exyz2，其中z＝z（x，y）是由x＋y＋z＋xyz＝0确定的隐函数，则fx′（0，1，－1）＝_”相关问题

  • 第1题：

    设有三元方程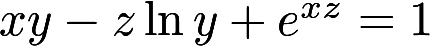 ，根据隐函数存在定理，存在点(0,1,1)的一个邻域，在此邻域内该方程

    A.只能确定一个具有连续偏导数的隐函数z=z(x,y)
    B.可确定两个具有连续偏导数的隐函数x=x(y,z)和z=z(x,y)
    C.可确定两个具有连续偏导数的隐函数y=y(x,z)和z=z(x,y)
    D.可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)

    答案：D
    解析：

  • 第2题：

    设z=z(x，y)是由方程x2+y2+z2=ez所确定的隐函数，求dz．


    答案：
    解析：

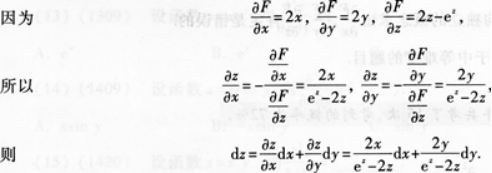
  • 第3题：

    设函数z=z(x，y)由方程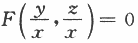确定，其中F为可微函数，且F'2≠0，则=

    A.Ax
    B.z
    C.-x
    D.-z

    答案：B
    解析：

  • 第4题：

    设Z=Z(x，Y)是由方程x+y3+z+e2=1确定的函数，求dz


    答案：
    解析：
    利用隐函数求偏导数公式，记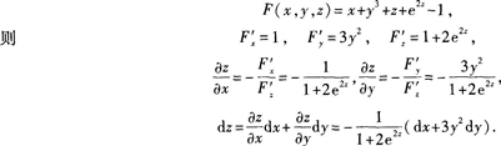

  • 第5题：

    单选题
    设f（x，y，z）＝exyz2，其中z＝z（x，y）是由x＋y＋z＋xyz＝0确定的隐函数，则fx′（0，1，－1）＝（　　）。
    A

    e

    B

    2e

    C

    0

    D

    1


    正确答案： B
    解析：
    构造函数F（x，y，z）＝x＋y＋z＋xyz，则有∂z/∂x＝－Fx′/Fz′＝－（1＋yz）/（1＋xy），（∂z/∂x）|（0，1，－1）＝0，又由f（x，y，z）＝exyz2，得fx′＝exyz2＋exy·2z·zx′，
    代入（0，1，－1），得fx′（0，1，－1）＝e0×1×（－1）2＋e0×1×2×（－1）×0＝1。

  • 第6题：

    单选题
    设X，Y是相互独立的随机变量，其分布函数分别为FX（x）、FY（y），则Z＝min（X，Y）的分布函数是（　　）。
    A

    FZ（z）＝max[FX（x），FY（y）]

    B

    FZ（z）＝min[FX（x），FY（y）]

    C

    FZ（z）＝1－[1－FX（x）][1＋FY（y）]

    D

    FZ（z）＝FY（y）


    正确答案： D
    解析：
    FZ（z）＝P{Z≤z}＝P{min（X，Y）≤z}＝1－P{min（X，Y）＞z}＝1－P{X＞z，Y＞z}＝1－P{X＞z}P{Y＞z}＝1－[1－FX（x）][1－FY（y）]，故应选C。

  • 第7题：

    单选题
    设函数z＝z（x，y）由方程F（x－az，y－bz）＝0所给出，其中F（u，v）任意可微，则a∂z/∂x＋（b∂z/∂y）＝（　　）。
    A

    1

    B

    2

    C

    3

    D

    4


    正确答案： A
    解析：
    根据偏导数的求解方法可知∂z/∂x＝－Fx′/Fz′＝－F1′/（―aF1′―bF2′），∂z/∂y＝－Fy′/Fz′＝－F2′/（―aF1′―bF2′），故a∂z/∂x＋（b∂z/∂y）＝－（aF1′＋bF2′）/（―aF1′―bF2′）＝1。

  • 第8题：

    单选题
    设函数z＝z（x，y）由方程F（x－az，y－bz）＝0所给出，其中F（u，v）任意可微，则a∂z/∂x＋（b∂z/∂y）＝（　　）。
    A

    0

    B

    1

    C

    2

    D

    4


    正确答案： B
    解析：
    根据偏导数的求解方法可知∂z/∂x＝－Fx′/Fz′＝－F1′/（―aF1′―bF2′），∂z/∂y＝－Fy′/Fz′＝－F2′/（―aF1′―bF2′），故a∂z/∂x＋（b∂z/∂y）＝－（aF1′＋bF2′）/（―aF1′―bF2′）＝1。

  • 第9题：

    单选题
    设z＝z（x，y）是由方程xz－xy＋ln（xyz）＝0所确定的可微函数，则∂z/∂y等于（　　）。[2013年真题]
    A

    －xz/（xz＋1）

    B

    －x＋1/2

    C

    z（－xz＋y）/[x（xz＋1）]

    D

    z（xy－1）/[y（xz＋1）]


    正确答案： B
    解析：
    将xz－xy＋ln（xyz）＝0两边对y求偏导，得xzy′－x＋x（z＋y·zy′）/（xyz）＝0，整理得zy′＝z（xy－1）/[y（xz＋1）]。

  • 第10题：

    单选题
    设函数z＝z（x，y）由方程z＝e2x－3z＋2y确定，则3∂z/∂x＋（∂z/∂y）＝（　　）。
    A

    0

    B

    1

    C

    2

    D

    4


    正确答案： B
    解析：
    构造函数F（x，y，z）＝z－e2x－3z－2y。则∂z/∂x＝－Fx′/Fz′＝2e2x－3z/（1＋3e2x－3z），∂z/∂y＝－Fy′/Fz′＝2/（1＋3e2x－3z），故3∂z/∂x＋（∂z/∂y）＝2。

  • 第11题：

    填空题
    设函数z＝z（x，y）由方程F（x－az，y－bz）＝0所给出，其中F（u，v）任意可微，则a∂z/∂x＋（b∂z/∂y）＝____。

    正确答案： 1
    解析：
    根据偏导数的求解方法可知∂z/∂x＝－Fx′/Fz′＝－F1′/（―aF1′―bF2′），∂z/∂y＝－Fy′/Fz′＝－F2′/（―aF1′―bF2′），故a∂z/∂x＋（b∂z/∂y）＝－（aF1′＋bF2′）/（―aF1′―bF2′）＝1。

  • 第12题：

    单选题
    由方程f（y/x，z/x）＝0确定z＝z（x，y）（f可微），则x∂z/∂x＋y∂z/∂y＝（　　）。
    A

    －z

    B

    z

    C

    －y

    D

    y


    正确答案： C
    解析：
    由f（y/x，z/x）＝0可得，∂z/∂x＝－[f1′·（－y/x2）＋f2′·（－z/x2）]/（f2′/x），∂z/∂y＝－（f1′/x）/（f2′/x），则x∂z/∂x＋y∂z/∂y＝－（―yf1′/x―zf2′/x＋yf1′/x）/（f2′/x）＝z。

  • 第13题：

    设随机变量X,Y相互独立,它们的分布函数为Fx(x),F(y),则Z=min{X,Y}的分布函数为().


    答案：C
    解析：
    FZ(z)=P(Z≤z)=P(min{X,Y}≤z)=1-P(min{X,Y}>z)　　=1-P(X>z,Y>z)=1-P(X>z)P(Y>z)
    　　=1-【1-P(X≤z)】【1-P(Y≤z)】=1-【1-FX(z)】【1-FY(z)】，选(C).

  • 第14题：

    设随机变量X~U（0，1)，Y~E（1），且X,Y相互独立，求Z=X+Y的密度函数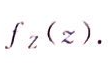


    答案：
    解析：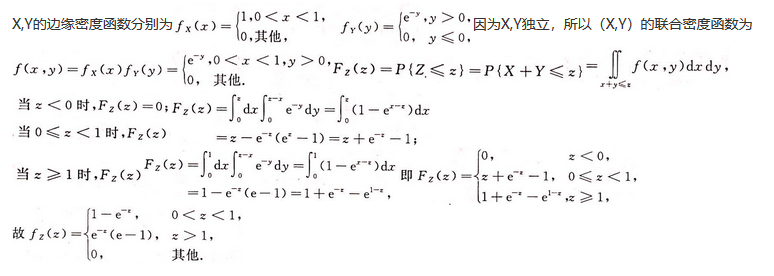

  • 第15题：

    设随机变量X与Y相互独立，且X服从标准正态分布N(0，1)，Y的概率分布为P{Y=0}=P{Y=1}=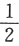.记Fz(z)为随机变量Z=XY的分布函数，则函数Fz(z)的间断点个数为

    A.A0
    B.1
    C.2
    D.3

    答案：D
    解析：

  • 第16题：

    设随机变量X与Y相互独立，且X~N（1，2），Y~N（0，1）。令Z=-Y+2X+3，则D（Z）=（）。


    正确答案:9

  • 第17题：

    单选题
    设函数z＝z（x，y）由方程z＝e2x－3z＋2y确定，则3∂z/∂x＋（∂z/∂y）＝（　　）。
    A

    2

    B

    1

    C

    e

    D

    0


    正确答案： A
    解析：
    构造函数F（x，y，z）＝z－e2x－3z－2y。则∂z/∂x＝－Fx′/Fz′＝2e2x－3z/（1＋3e2x－3z），∂z/∂y＝－Fy′/Fz′＝2/（1＋3e2x－3z），故3∂z/∂x＋（∂z/∂y）＝2。

  • 第18题：

    填空题
    设函数z＝z（x，y）由方程z＝e2x－3z＋2y确定，则3∂z/∂x＋∂z/∂y＝____。

    正确答案： 2
    解析：
    方程两边同时对x求偏导，则∂z/∂x＝e2x－3z（2－3∂z/∂x），可得∂z/∂x＝2e2x－3z/（1＋3e2x－3z）。同理∂z/∂y＝e2x－3z（－3∂z/∂y）＋2，可得∂z/∂y＝2/（1＋3e2x－3z），所以3∂z/∂x＋∂z/∂y＝6e2x－3z/（1＋3e2x－3z）＋2/（1＋3e2x－3z）＝2（1＋3e2x－3z）/（1＋3e2x－3z）＝2。

  • 第19题：

    填空题
    设z＝f（xy，x/y）＋g（y/x），其中f、g均可微，则∂z/∂x＝____。

    正确答案： yf1′+f2′/y-yg′/x2
    解析：
    设f1′为函数f（u，v）对第一中间变量的偏导，f2′为函数f（u，v）对第二中间变量的偏导，g′为函数g对x的导数。则∂z/∂x＝∂f（xy，x/y）/∂x＋∂g（y/x）/∂x＝f1′y＋f2′·（1/y）＋g′·（－y/x2）＝f1′y＋f2′/y－yg′/x2。

  • 第20题：

    单选题
    设z＝φ（x2－y2），其中φ有连续导数，则函数z满足（　　）。
    A

    x∂z/∂x＋y∂z/∂y＝0

    B

    x∂z/∂x－y∂z/∂y＝0

    C

    y∂z/∂x＋x∂z/∂y＝0

    D

    y∂z/∂x－x∂z/∂y＝0


    正确答案： D
    解析：
    令u＝x2－y2，则z＝φ（u），∂z/∂x＝φ′（u）·2x＝2xφ′（u），∂z/∂y＝－2yφ′（u），故y∂z/∂x＋x∂z/∂y＝0。

  • 第21题：

    单选题
    设方程x＋z＝yf（x2－z2）（其中f可微）确定了z＝z（x，y），则z∂z/∂x＋y∂z/∂y＝（　　）。
    A

    x

    B

    y

    C

    z

    D

    yf（x2－y2）


    正确答案： C
    解析：
    由x＋z＝yf（x2－z2），可得∂z/∂x＝－（1－y·2xf′）/（1＋2yzf′），∂z/∂y＝－（－f）/（1＋2yzf′），故有（z∂z/∂x）＋（y∂z/∂y）＝（x－yf＋2xyzf′＋yf）/（1＋2yzf′）＝x。

  • 第22题：

    填空题
    设f（u，v）是二元可微函数，z＝f（y/x，x/y），则x∂z/∂x－y∂z/∂y＝____。

    正确答案： 2(-yf1′/x+xf2′/y)
    解析：
    设f1′为函数f（u，v）对第一中间变量的偏导，f2′为函数f（u，v）对第二中间变量的偏导，则∂z/∂x＝f1′·（－y/x2）＋f2′·（1/y），∂z/∂y＝f1′·（1/x）＋f2′·（－x/y2），x∂z/∂x－y∂z/∂y＝2（－yf1′/x＋xf2′/y）。

  • 第23题：

    单选题
    设三元函数xy－zlny＋exz＝1，根据隐函数存在定理，存在点（0，1，1）的一个邻域，在此邻域内该方程（　　）。
    A

    只能确定一个具有连续偏导数的隐函数z＝z（x，y）

    B

    可确定两个具有连续偏导数的隐函数y＝y（x，z）和z＝z（x，y）

    C

    可确定两个具有连续偏导数的隐函数x＝x（y，z）和z＝z（x，y）

    D

    可确定两个具有连续偏导数的隐函数x＝x（y，z）和y＝y（x，z）


    正确答案： C
    解析：
    构造函数F（x，y，z）＝xy－zlny＋exz－1，则Fx′＝y＋zexz，Fy′＝x－（z/y），Fz′＝－lny＋xexz。Fx′（0，1，1）＝2≠0，Fy′（0，1，1）＝－1≠0，Fz′（0，1，1）＝0。
    故根据隐函数的存在定理可知，方程xy－zlny＋exz＝1能确定x是y、z的具有连续偏导数的函数x＝x（y，z）；y是x、z的具有连续偏导数的函数y＝y（x，z）。因为Fz′（0，1，1）＝0不能满足定理成立的条件，故不能确定z是x、y的具有连续偏导数的隐函数z＝z（x，y）。

相关内容