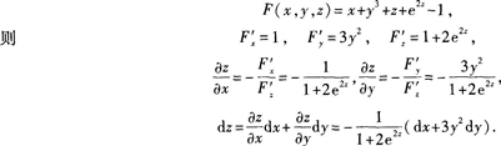(本题满分8分) 设函数z=z(x,y)是由方程x+y3+z+e2x=1所确定的隐函数,求dz.
题目
(本题满分8分) 设函数z=z(x,y)是由方程x+y3+z+e2x=1所确定的隐函数,求dz.
相似考题
更多“(本题满分8分) 设函数z=z(x,y)是由方程x+y3+z+e2x=1所确定的隐函数,求dz. ”相关问题
-
第1题:
求由方程2x2+y2+z2+2xy-2x-2y-4z+4=0确定的隐函数的全微分.答案:解析:
-
第2题:
设z=z(x,y)是由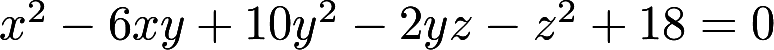 确定的函数,求
确定的函数,求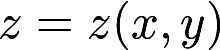 的极值点和极值答案:解析:
的极值点和极值答案:解析:
-
第3题:
设 u=exyz2,u=exyz2, 其中 z=z(x,y)z=z(x,y) 是由方程 x+y+z=xyzx+y+z=xyz 确定的隐函数,则 ∂u∂x∣∣∣(0,1,−1)=
A.5
B.-3
C.3
D.1
D -
第4题:
设z=z(x,y)是由方程x2+y2+z2=ez所确定的隐函数,求dz.答案:解析:
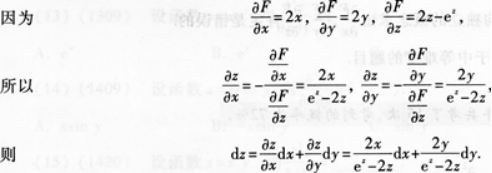
-
第5题:
设Z=Z(x,Y)是由方程x+y3+z+e2=1确定的函数,求dz答案:解析:利用隐函数求偏导数公式,记