2021年河南专升本《高数》真题(含答案)
普通高等学校2013年应届本科毕业生可以报名参加国家司法考试吗?
可以。
2009年高职(专科)院校占全国普通高等学校和成人高等学校的比重比本科院校高( )个百分点。 A.4.59 B.4.65 C.4.92 D.5.13
2009年高职(专科)院校(1246-31)所,本科院校(1112-22)所,普通高等学校和成人高
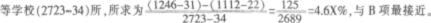
高职(高专)毕业生参加“三支一扶”,服务期满考核合格的,可免试入读( )。
A.成人高等学历教育专科
B.普通专科
C.普通本科
D.成人高等学历教育专科起点本科
普通高等学校在校学生数指( )。
A.在普通高等学校接受本科教育的学生数
B.在普通高等学校接受本专科教育的学生数
C.在普通高等学校接受本专科和硕士研究生教育的学生数
D.在普通高等学校接受本专科和硕士、博士研究生教育的学生数
2021 年河南省普通高等学校年河南省普通高等学校 专科毕业生进入本科阶段学习考试专科毕业生进入本科阶段学习考试 高等数学高等数学 题号题号 一一 二二 三三 四四 五五 总分总分 分数分数 50 30 50 14 6 150 注意事项:注意事项: 答题前:考生务必将自己的姓名、考场号、座位号、考生号填写在答题卡上答题前:考生务必将自己的姓名、考场号、座位号、考生号填写在答题卡上 本卷的试题答案必须答在答题卡上,答在卷上无效本卷的试题答案必须答在答题卡上,答在卷上无效 选题分析:选题分析: 易(42 分) 中(73 分) 难(35 分) 选择: 1/2/4/6/8/9/10/12/15/18/21 填空: 26/28/30/32/37 计算: 41/43 应用: 证明: 选择: 3/5/7/11/13/14/16/17/20/22/ 23/24/25 填空: 27/29/31/34/35/36/38/39 计算: 42/44/46/48/50 应用: 证明: 53 选择: 19 填空: 33/40 计算: 45/47/49 应用: 51/52 证明: 一、一、选择题(选择题(每小题每小题 2 分,共分,共 50 分分) 在每小题的四个备选答案中选一个正确答案,用铅笔把答题卡上对应题目的答案标号涂黑在每小题的四个备选答案中选一个正确答案,用铅笔把答题卡上对应题目的答案标号涂黑. 1.对称区间上( )f x是奇函数,( )g x是偶函数,下列函数是奇函数的是( ) A.4()f x 2021年河南专升本高数真题(含答案)第 1 页,共 18 页 B.( )( )g xf x+ C.( ) ( )g x f x D.()gx 2.极限0tan3lim2xxx=( ) A.32 B.23 C.0 D. 3.当+x时,下列变量不是无穷大量的是( ) A.42132+xx B.xlg C.x3 D.xarctan 4.00,cos,sin2)(+=xxxxxxxxf,则0=x处是)(xf的( ) A.无穷间断点 B.可去间断点 C.跳跃间断点 D.振荡间断点 5.极限)4421(lim22xxx的值为( ). 2021年河南专升本高数真题(含答案)第 2 页,共 18 页 A.41 B.21 C.41 D. 6.下列关于函数)(xfy =在点0 x的命题不正确的是( ). A.可导必连续 B.可微必可导 C.可导必可微 D.连续必可导 7.设函数1212nnnnyxa xa xa=+,则( )ny=( ). A.na B.!n C.0 D.!nn a 8.设( )ln 1f xx=+,则= ) 1 (f( ). A.2 B.1 C.12 D.14 9.设函数)(xfy =在点1=x处可导,且21( )(1)lim31xf xfx=,则(1)f =( ). A.2 B.3 C.6 D.12 2021年河南专升本高数真题(含答案)第 3 页,共 18 页 10.曲线)4(3=xxy在区间)4,(内的特性是( ). A.单调递减且为凸 B.单调递减且为凹 C.单调递增且为凸 D.单调递增且为凹 11.下列等式中正确的是( ). A.2211=dx B.21112=+dxx C.21112=dxx D.0)cos(sin11=+dxxx 12.已知+=CxFdxxf)()(,则=dxxfx)(ln1( ). A.)(ln xF B.CxF+)(ln C.CxxF+)(ln D.CxFx+)(ln1 13.下列式子正确的是( ). A.)()(xfdxxfdxd= B.)()(xfdxxfd= C.( )( )dfx dxf xCdx=+ D.)()(xfdxxf= 14.平面230 xy+=的位置是( ). A.平行于xOy面 2021年河南专升本高数真题(含答案)第 4 页,共 18 页 B.平行于z轴,但不通过z轴 C.垂直于z轴 D.通过z轴 15.方程222222xyzabc+=所表示的曲面为( ). A.椭圆抛物面 B.椭圆锥面 C.椭球面 D.椭圆柱面 16.下列广义积分中发散的是( ). A.22dxx B.111xdx C.+0dxex D.+22)(ln1dxxx 17.常数0a ,222()aaxx axdx+=( ). A.0 B.3a C.332a D.323a 18.下列方程中为一阶线性微分方程的是( ). A.2()yxyxy+= 2021年河南专升本高数真题(含答案)第 5 页,共 18 页 B.2()0 xyyy+= C.2x yyx+= D.20yyy+= 19. 已 知12yx=是2yyx+=的 解 ,2xye=是2xyye+=的 解 , 则 微 分 方 程22xyyxe+=+的通解是( ). A.2xxe+ B.12cossin2xCxCxxe+ C.12cossinxCxCxe+ D.12cossin2CxCxx+ 20.若函数( , )f x y在点00(,)xy处具有一阶及二阶偏导数且取极小值,则( ). A.0000(,)(,)0 xyfxyfxy= B.若00(,)xy是D内唯一极值点,则必为最小值点 C.2000000(,)(,)(,)0 xxyyxyfxyfxyfxy,且00(,)0 xxfxy D.2000000(,)(,)(,)0 xxyyxyfxyfxyfxy,且00(,)0 xxfxy= . 35.函数4xxyee=+的极值点坐标是 . 36.曲面53zezxy+=在点(2,1,0)处切平面方程是 . 37.设二元函数22zxyy=+,则(3,1)dz= . 38.函数lnsinyx=在区间233,上满足罗尔定理的的值是 . 39.L为正向圆周22(1)4xy+=,33(2)()Lyx dxxy dy+= . 40.将函数24( )65f xxx=+展开为x的幂级数为 . 三、计算题(每小题三、计算题(每小题 5 分,共分,共 50 分)分) 41.求极限0ln(1 5 sin )lim1 cosxxxx+. 2021年河南专升本高数真题(含答案)第 8 页,共 18 页 42.若极限23lim()01xxaxbx+=,求, a b的值. 43.设函数arctanyx=,求dydx及1xdydx=. 44.求曲线23ln(1)yx=+的拐点及凹凸区间. 45.计算不定积分311 1dxx+ +. 46.设2cos,0( )21,0 xxf xxx=+,21(1)f xdx. 47.过点( 3, 2,0)且与直线21:111xyzL=垂直相交的直线方程. 48.设二元函数2arcsin()3xzxyy=,求2zzxyyxy. 49.计算二重积分yxDIe dxdy=,其中积分区域D由直线yx=,0y =,3x =围成. 50.判断级数11 3 3 5(21)5!nnnn= 的收敛性. 四、应用题(每小题四、应用题(每小题 7 分,共分,共 14 分)分) 51.过坐标原点作曲线xye=的切线,求: (1)该切线的方程; (2)由曲线、切线及y轴所围成的平面图形绕x轴旋转一周而成的旋转体的体积. 52.质量为1g的质点受外力作用作直线运动, 该外力和时间成正比, 与质点运动的速度成反比.在10st =时,速度100cm/sv =,外力22g cm/sF =,问30st =时,质点的速度是多少?(658.062,计算结果取整数,注:Fma=,a为加速度) 五、证明题(每小题五、证明题(每小题 6 分,共分,共 6 分)分) 2021年河南专升本高数真题(含答案)第 9 页,共 18 页 53.证明多项式3( )26f xxxa=+在区间 1,1上至多有一个零点,其中a为任意实数. 20212021 年河南省普通高等学校年河南省普通高等学校 专科毕业生进入本科阶段学习考试专科毕业生进入本科阶段学习考试 高等数学高等数学 【参考答案】【参考答案】 一、选择题(每小题一、选择题(每小题 2 2 分,共分,共 5050 分分) 1.【答案】C 【解析】由函数奇偶性结论可得,奇函数偶函数=奇函数,故选 C. 2.【答案】A 【解析】本题考察求“00”型极限,利用等价代换可得:00tan333limlim222xxxxxx=. 3.【答案】D 【解析】lim arctan2xx+= ,根据无穷大量的定义知,故选 D. 4.【答案】C 【解析】00lim( )limcos0 xxf xxx+=,00sinlim( )lim(2)1xxxf xxx=+=, 在0 x =左右极限存在且00lim( )lim( )xxf xf x+,所以0 x =为跳跃间断点,故选 C. 5.【答案】A 【解析】本题考察求“”型极限,2222214211lim()limlim24424xxxxxxxx=+,故选 A. 6.【答案】D 【解析】根据可微 可导 连续的关系,知连续不一定可导,故选 D. 7.【答案】B 【解析】本题考查高阶导数,由结论知,( )!nyn=,故选 B. 8.【答案】D 【解析】111( )2(1)12 1fxxxx=+,1(1)4f =,故选 D. 2021年河南专升本高数真题(含答案)第 10 页,共 18 页 9.【答案】C 【解析】211( )(1)( )(1)1limlim(1)31(1)(1)2xxf xff xffxxx=+,所以(1)6f =,故选 C. 10.【答案】B 【解析】343(4)4yxxxx=,32412yxx =,在(, 4) 内0y,所以曲线在(, 4) 内是凹函数,故选 B. 11.【答案】C 【解析】根据定积分几何意义,由被积函数21(0)yxy=知定积分1211x dx表示以原点为圆心、1为半径的上半圆面积,即1211122x dxS=圆,故选 C. 12.【答案】B 【解析】根据已知条件,由不定积分第一换元法得: 1(ln )(ln ) (ln )(ln )fx dxfx dxFxCx=+,故选 B. 13.【答案】A 【解析】 利用微积分互逆运算: B 选项( )( )df x dxf x dx=, C 选项( )( )dfx dxfxdx=,D 选项( )( )fx dxf xC=+,故选 A. 14.【答案】B 【解析】平面230 xy+=法向量(2,1,0)n=,z轴方向向量(0,0,1)s=,0n s =,即平面230 xy+=与z轴平行;代入原点,得2 0030 +,即平面不经过z轴;故选 B. 15.【答案】B 【解析】方程222222xyzabc+=为椭圆锥面的方程式,故选 B. 16.【答案】A 【解析】2020220220lnlndxdxdxxxxxx=+=+,不存在,即发散,故选 A. 17.【答案】D 2021年河南专升本高数真题(含答案)、第 11 页,共 18 页 【解析】22222233022()033aaaaaaaxx axdxx dxx ax dxxa+=+=+=,故选 D. 18.【答案】C 【解析】根据微分方程阶和线性的定义,可得2x yyx+=为一阶线性微分方程,故选 C. 19.【答案】B 【解析】根据二阶线性微分微分方程的性质可得,1222xyyxe+=+为微分方程22xyyxe+=+的解;设二阶线性齐次微分方程为0yy+=,特征方程为210r + =,ri= ,得二阶线性齐次微分方程的通解为:12cossinyCxCx=+,故微分方程22xyyxe+=+的通解为12cossin2xCxCxxe+,故选 B. 20.【答案】C 【解析】( , )f x y在点00(,)xy处有一阶、二阶偏导数,且取得极小值,根据二元极值的充分条件知选项 C 正确,故选 C. 21.【答案】C 【解析】22zxyx=,22zx y= ,2(1,2)2zx y= ,故选 C. 22.【答案】A 【解析】 与(2, 1)l=同向的单位向量21(,)55e=, 又因为( 1,2)4xf =,( 1,2)2yf = ,故(2,
B. 3
C. 4
D. 5
B. 经区招生办公室专科统一录取且取得全日制专科学历的毕业生士兵,可以参加全军统一组织的本科层次招生考试
C. 录取的入有关军队院校学习
D. 学制4年
E. 毕业合格的列入年度生长干部毕业学员分配计划
B.在普通高等学校接受本专科教育的学生数
C.在普通高等学校接受本专科和硕士研究生教育的学生数
D.在普通高等学校接受本专科和硕士、博士研究生教育的学生数
B.师范高等学校
C.普通本科学校
D.重点本科学校
B.师范高等学校
C.普通本科学校
D.重点本科学校
