卓越联盟自主招生数学试题及答案精校版+完整版
已知向量a,b,c是三个具有公共起点的非零向量,且|a|=2|b|=2,又a·b=-1, 〈a-c,b-c 〉=π/3 ,则当|a-c|=7时,向量a与c的夹角是____.
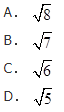
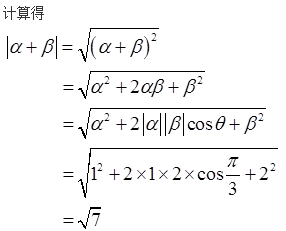
B.
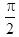
C.
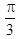
D.
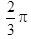
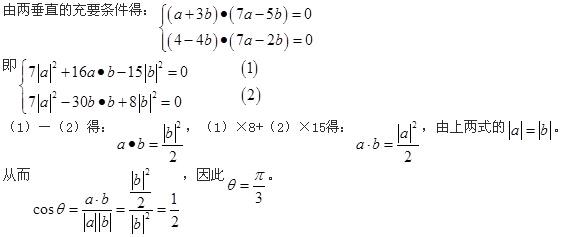
B.
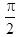
C.
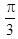
D.
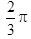
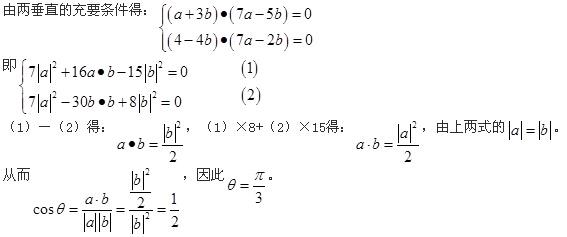
B.
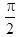
C.
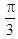
D.
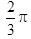
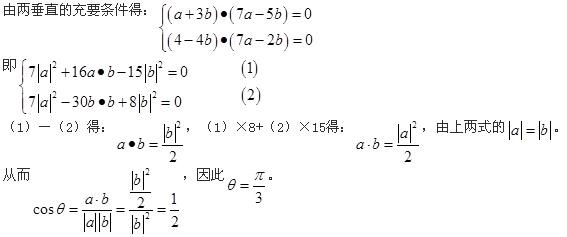
摘要:2011年卓越联盟自主招生数学试题(1)向量a,b均为非零向量,(a-2b)⊥a,(b-2a)⊥b,则a,b的夹角为(A)6(B)3(C)23(D)56tan()(2)已知sin2(+)=nsin2,则tan()22等于(A)n1n1(B)nn1(C)nn1(D)n1n1(3)在正方体ABCD—A1B1C1D1中,E为棱AA1的中点,F是棱A1B1上的点,且A1F:FB1=1:3,则异面直线EF与BC1所成角的正弦值为(A)153(B)155(C)53(D)55z22z2(4)i为虚数单位,设复数z满足|z|=1,则z1i的最大值为(A)2-1(B)2-2(C)2+1(D)2+2(5)已知抛物线的顶点在原点,焦点在x轴上,△ABC三个顶点都在抛物线上,且△ABC的重心为抛物线的焦点,若BC边所在直线的方程为4x+y-20=0,则抛物线方程为(A)y2=16x(B)y2=8x(C)y2=-16x(D)y2=-8x(6)在三棱锥ABC—A1B1C1中,底面边长与侧棱长均等于2,且E为CC1的中点,则点C1到平面AB1E的距离为(A)3(B)2|x|(C)32(D)22(7)若关于x的方程x4=kx2有四个不同的实数解,则k的取值范围为() 1(B)(4,1)(A)(0,1)1(C)(4,+∞)(D)(1,+∞)(8)如图,△ABC内接于⊙O,过BC中点D作平行于AC的直线l,l交AB于E,交⊙O于G、F,交⊙O在A点的切线于P,若PE=3,ED=2,EF=3,则PA的长为(A)5(B)6(C)7(D)2
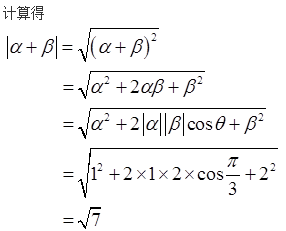
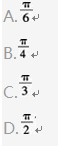
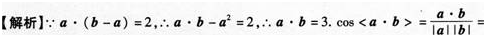
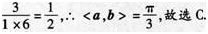
B.
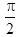
C.
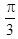
D.
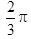
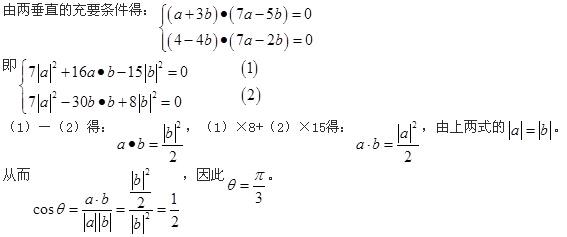
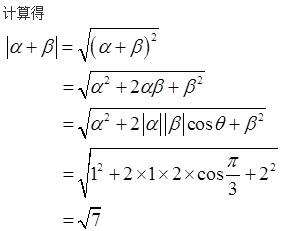
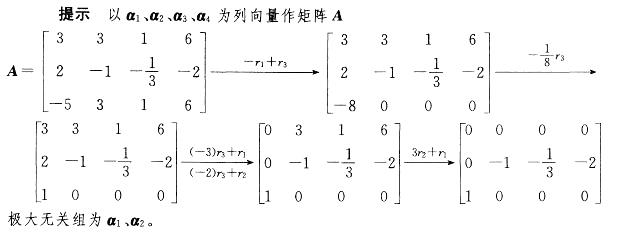
B.a3,a4
C.a1,a2
D.a2,a3
更多 “卓越联盟自主招生数学试题及答案精校版+完整版” 相关考题
相关内容
最新试卷
热门试卷
- 2022造价工程师《造价管理》真题测试强化卷和答案90-
- 金属非金属矿山(地下矿山)主要负责人安全生产考试试题测试强化卷及答案(第4次)-
- 2022造价工程师《造价管理》真题测试强化卷和答案11-
- 2022造价工程师《造价管理》真题测试强化卷和答案(第98版)-
- 2022造价工程师《造价管理》真题测试强化卷和答案(第74卷)-
- 2022造价工程师《造价管理》真题测试强化卷和答案(第93版)-
- 金属非金属矿山(地下矿山)主要负责人安全生产考试试题测试强化卷及答案(第57卷)-
- 2月7日作业及答案:高三地理每日一题-
- 面试每日一练模拟题及参考答案03.03-
- 2020年中级经济师考试试题每日一练(11.28)-
