北语19春《概率论与数理统计》精选试题与答案
A、3/5
B、3/4
C、1/2
D、3/10
甲箱中有5个正品,3个次品;乙箱中有4个正品,3个次品。从甲箱中任取3个产品放入乙箱,然后从乙箱中任取1个产品,则这个产品是正品的概率为( )。
A.0.176
B.0.2679
C.0.3342
D.0.5875
解析:设B={从乙箱中取得正品},A1={从甲箱中取出3个正品},A2={从甲箱中取出2个正品1个次品},A3={从甲箱中取出1个正品2个次品},A4={从甲箱中取出3个次品},显然A1、A2、A3、A4都是互斥的,所以B=B(A1+A2+A3+A4)。故P(B)=P(BA1+BA2+BA3+BA4)=P(A1)P(B|A1)+P(A2)P(B|A2)+P(A3)P(B|A3)+P(A4)P(B|A4)=(10/56)×(7/10)+(30/56)×(6/10)+(15/56)×(5/10)+(1/56)×(4/10)=0.5875。
参考答案:P=3/10×2/9×1/8=1/120
(2)P´=3/10×3/10×3/10=27/1000
分析:对于第一题,第一次取到次品的概率为3/10,第二次再取时次品只有二件了,故为2/9,由此而类推的第三次。对于第二题,由于不放回,故每次取到次品的概率都为3/10。
一口袋装有6只球,其中4只白球、2只红球。从袋中取球两次,每次随机地取一只。采用不放回抽样的方式,取到的两只球中至少有一只是白球的概率()
A、4/9
B、1/15
C、14/15
D、5/9
估计量的有效性是指( )。A.估计量的方差比较大B.估计量的置信区间比较大C.估计量的方差比较小D.估计量的置信区间比较小正确答案:C
在二点分布中,随机变量X的取值()0、1A.只能B.可以取C.不可以D.以上都不对正确答案:B
一个袋内装有10个球,其中有4个白球,6个红球,采取不放回抽样,每次取1件,则第二次取到的是白球的概率是()A.0.3B.0.6C.0.7D.0.4正确答案:D
袋中有50个乒乓球,其中20个黄的,30个白的,现在两个人不放回地依次从袋中随机各取一球。则第二人取到黄球的概率是A.1/5B.2/5C.3/5D.4/5正确答案:B
设试验E为从10个外形相同的产品中(8个正品,2个次品)任取2个,观察出现正品的个数。 试问E的样本空间是( )A.A0B.B1C.C1,2D.D0,1,2正确答案:D
全国国营工业企业构成一个()总体A.有限B.无限C.一般D.一致正确答案:A
测量轴的直径之长度不会引起系统误差,而直径长度的偶然误差这一随机变量X服从均方差σ=10毫米的正态分布。则测量轴的直径的长度发生的偏差绝对值不超过15毫米的概率为()A.0.5547B.0.8664C.0.7996D.0.3114正确答案:B
设离散型随机变量X的分布为 X5234 P0.40.30.10.2则它的方差为()。A.14.36B.15.21C.25.64D.46.15正确答案:B
一个袋内装有10个球,其中有3个白球,5个红球,2个黑球采取不放回抽样,每次取1件,则第二次取到的是白球的概率是()
A、0.6
B、0.5
C、0.4
D、0.3
(1)第二次取到的也是正品的概率;(2)两次取到的都是正品的概率;
(3)第二次取到的是正品的概率.

A. 0. 176 B. 0. 2679 C. 0. 3342 D. 0. 5875

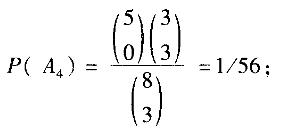
P(B A1) =7/10,P(B A2) =6/10,P(B A3) =5/10,P(B A4) =4/10;
故P(B) =P(BA1+BA2 + BA3+ BA4) =P(A1)P(B A1) +P(A2)P(B A2) +P(A3)P (B A3) +P(A4)P(B A4) = (10/56) x (7/10) + (30/56) x (6/10) + (15/56) x (5/ 10) + (1/56) x (4/10) =0.5875。

(方法二)只考虑第二个人取得的球,这50个球中每一个都会等可能地被第二个人取到,而取到黄球的可能有20个,故所求概率为

 ②求二维随机变量(X,Y)的概率分布。
②求二维随机变量(X,Y)的概率分布。
