十进制数5的单精度浮点数IEEE754代码为()。A.01000000101000000000000000000000 B.11000000101000000000000000000000 C.00100000101000000000000000000000 D.01100000101000000000000000000000

题目
十进制数5的单精度浮点数IEEE754代码为()。

A.01000000101000000000000000000000
B.11000000101000000000000000000000
C.00100000101000000000000000000000
D.01100000101000000000000000000000
相似考题

1.SSEintrinsics_mm_load_ps命令的功能是____。A、对齐向量读取单精度浮点数B、未对齐向量读取单精度浮点数C、对齐向量读取双精度浮点数D、未对齐向量读取双精度浮点数

2.将十进制数0.84375表示成符合IEEE754标准的32位浮点数的是【 】。

3.IEEE754浮点数x的二进制存储格式为(41360000)H,其对应的十进制值为( )A.11.5B.11.375C.11.355D.10.385

4.●在Pentium微处理器中，浮点数的格式采用IEEE754标准。假设一个规格化的32位浮点数如下：1 10000011 00101100000000000000000该数的十进制数值是 (29) 。(29) A．-2．75B．-16．75C．-20．75D．-18．75

更多“十进制数5的单精度浮点数IEEE754代码为()。A.01000000101000000000000000000000 B.11000000101000000000000000000000 C.00100000101000000000000000000000 D.01100000101000000000000000000000”相关问题

  • 第1题：

    在Pentium微处理器中，浮点数的格式采用IEEE754标准。假设一个规格化的32位浮点数如下 1 10000011 00101100000000000000000 该数的十进制数值是

    A．-2.75

    B．-16.75

    C．-20.75

    D．-18.75


    正确答案：D
    解析：Pentium微处理器中浮点数格式完全符合IEEE754标准，它表示成如下形 式： (-1)s2E(b0b1b2b3…bp-1)，其中(-1)s是该数的符号位，s=0表示此数为正， 1表示此数为负。E是指数， (b0b1b2b3…bp-1)是尾数，使用原码表示，表示隐 含的小数点，p是尾数的长度。本题计算如下：s=l，该数为负，先计算指数，因为 E=10000011=(131)10，所以指数=131-127=4。再计算尾数。因为规格化的尾数是 -1．001011，所以该浮点数的数值为：-1．001011×24=-10010．11=(-18．75)10

  • 第2题：

    下面关于计算机浮点数的叙述中，正确的是

    A．浮点数的绝对值不能大于1010

    B．十进制整数不能用浮点数精确表示

    C．Pentium微处理器中的浮点数采用40位二进制编码

    D．Pentium微处理器中浮点数的格式采用IEEE754标准


    正确答案：D
    解析：浮点数的长度可以是32位、64位甚至更长，位数越多，可表示的数值的范围越大，精度也越高，选项A说法错误。十进制整数可以用浮点数精确表示，选项B说法错误。Pentium微处理器中的浮点数有三种不同类型，分别是：单精度浮点数(32位)、双精度浮点数(64位)和扩充精度浮点数(80位)，选项C说法错误。Pentium微处理器中浮点数的格式采用IEEE754标准，选项D正确。

  • 第3题：

    下列是关于浮点数的说法：

    ①浮点数编码方式不但扩大了数值的表示范围，而且也增加了数据表示的数量。

    ②IEEE754是关于浮点数定义和规格化的工业标准，制定这一标准的目的是提高浮点数的运算速度和精度。

    ③IEEE754标准中求移码的偏移量跟求普通移码所采用的偏移量相差1。

    ④在完整的最终的编码中，若阶码总编码位数为R(包括阶码符号位)，尾数总编码位数为w(包括符号位)，那么IEEE754标准下的规格化浮点数的最大负数为。

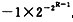    其中，正确的说法有(35)。

    A．1

    B．2

    C．3

    D．4


    正确答案：A
    解析：浮点数编码方式虽然扩大了数值的表示范围，但并未增加数据表示的数量。IEEE754是关于浮点数定义和规格化的工业标准，制定这一标准的目的是为了便于程序从一类处理器移植到另一类处理器上，也为了促进研制更为复杂的数值运算程序，并不是为了提高浮点数的运算速度和精度。IEEE754标准中求移码的偏移量跟求普通移码所采用的偏移量相差1。例如，总编码位数为8位(包括1位符号位，7位数值位)，那么求十进制真值7的普通移码时偏移量为27，移码为7+27=10000111B；而在IEEE754标准中，求特殊移码的偏移量改为2n-1，因此，真值7在IEEE754标准中的特殊移码为：7+27-1=10000110B。在完整的最终的编码中，若阶码总编码位数为R(包括阶码符号位)，尾数总编码位数为w(包括符号位)，那么IEEE754标准下的规格化浮点数的最大负数应为。

  • 第4题：

    IEEE754标准规定：单精度浮点数的最高位为符号位，后面跟8位经偏移的阶码移码，偏移量为+127。尾数用原码表示，且把尾数规格化为1. xxx…x(x为0或1)，并将1去掉，尾数用23位表示。根据该标准，十进制数+178. 125的规格化表示形式为______。

    A．0 10000110 01100100010000000000000

    B．0 10000111 01100100010000000000000

    C．1 10000100 01100100010000000000000

    D．0 10000110 11100100010000000000000


    正确答案：A
    解析：IEEE754标准在表示浮点数时，每个浮点数均由三部分组成：符号位S、指数部分E和尾数部分M。浮点数一般采用以下两种基本格式：(1)单精度格式(32位)：除去符号位1位后，E占8位，M占23位。(2)双精度格式(64位)：E占11位，M占52位。在IEEE754标准中，约定小数点左边隐含有一位1，这样实际上使尾数的有效位数为24位，即尾数真值形如1.M。指数的值在这里称为阶码，为了表示指数的正负，阶码部分采用移码表示，移码值为127。对于规格化浮点数而言，阶码值即从1～254变为-126～+127。将十进制数+178.125化为规格化浮点数的步骤如下：第一步：正数的符号位为0第二步：178转换为二进制数，(178)10=(10110010)2第三步：0.125转换为二进制数，(0.125)10=(0.001)2第四步：合并结果得到，(178.125)10=(10110010.001)2第五步：对二进制数进行规格化处理，10110010.001=1.0110010001×27，隐含小数点及其左边的1，化为原码，并扩展至23位得：01100100010000000000000。第六步：求阶码，上述表示的指数为7，而单精度浮点数规定的指数的偏移量为127，127+7=134，化为二进制得10000110。最后，我们得到+178.125的规格化表示形式为01000011001100100010000000000000

  • 第5题：

    IEEE754标准浮点数的尾数采用()机器数形式。

    A.原码
    B.补码
    C.移码
    D.反码

    答案：A
    解析：
    IEEE754标准浮点数的尾数采用原码表示，选A项。

  • 第6题：

    若IEEE754单精度格式为（-1）s×（1.M）×2E-127，则十进制数0.625表示成754标准的十六进制数据为（）。

    • A、3F200000H
    • B、BF200000H
    • C、3F400000H
    • D、BF400000H

    正确答案:A

  • 第7题：

    在IEEE754标准中，浮点数的表示采用单精度格式是（）位。

    • A、64
    • B、32
    • C、16
    • D、128

    正确答案:B

  • 第8题：

    某数为IEEE754单精度浮点数格式表示为45100000H，则该数的值是（）

    • A、1.125×210
    • B、1.125×211
    • C、-1.125×211
    • D、-1.125×210

    正确答案:B

  • 第9题：

    将下列十进制数转换为IEEE754单精度浮点数格式： （1）＋36.75 （2）－35/256


    正确答案:（1）+36.75=+100100.11B=1.0010011*25
    符号：0
    阶码：5+127=132=10000100
    尾数：00100110000000000000000
    单精度浮点数表示形式为01000010000100110000000000000000B＝42130000H
    （2）-35/256=-100011*2-8=-1.00011*2-3
    符号：1
    阶码：-3+127=124=01111100
    尾数：000110000000000000000000
    单精度浮点数表示形式为10111110000011000000000000000000B＝B.E0C0000H

  • 第10题：

    单选题
    某数为IEEE754单精度浮点数格式表示为45100000H，则该数的值是（）
    A

    1.125×210

    B

    1.125×211

    C

    -1.125×211

    D

    -1.125×210


    正确答案： A
    解析： 暂无解析

  • 第11题：

    问答题
    已知内存中32位位模式为“1  1000 0001   1110 0000 0000 0000 0000 000”当该位模式表示的是单精度浮点数，假定浮点数编码采用Excess-127表示指数部分，通过计算解码出该浮点数对应的十进制数值。写出计算步骤。

    正确答案： 符号为负号    位移量=129-127=2  111.1000 0000 0000 0000 0000 0
    该数绝对值是7.5     该数是-7.5
    解析： 暂无解析

  • 第12题：

    问答题
    将下列十进制数转换为IEEE754单精度浮点数格式： （1）＋36.75 （2）－35/256

    正确答案： （1）+36.75=+100100.11B=1.0010011*25
    符号：0
    阶码：5+127=132=10000100
    尾数：00100110000000000000000
    单精度浮点数表示形式为01000010000100110000000000000000B＝42130000H
    （2）-35/256=-100011*2-8=-1.00011*2-3
    符号：1
    阶码：-3+127=124=01111100
    尾数：000110000000000000000000
    单精度浮点数表示形式为10111110000011000000000000000000B＝B.E0C0000H
    解析： 暂无解析

  • 第13题：

    Pwntium 微处理品器中的浮点数复合IEEE754标准，设一个单精度浮点数为 01000000011100000000000000000000 这个浮点数的阶码是

    A．10000000

    B．01000000

    C．00000001

    D．00000011


    正确答案：A

  • 第14题：

    某计算机中一个16位的二进制代码1101 11100101 1000，它若表示的是一个浮点数，该浮点数格式如下：

    其中，阶码为移码(又叫增码)，基数为2，尾数用补码表示，则该浮点数的值(十进制)是【 】。


    正确答案：-6.625
    -6.625

  • 第15题：

    符合IEEE754标准的单精度浮点数0 10000101 1000100 10000000 00000000所表示的十进制数为【 】。


    正确答案：98.25
    98.25 解析：IEEE754标准中采用32位二进制表示浮点数，其表示方法(从左至右)分别是：1位符号+8位指数位+23位尾数。这里最高位是0，因此是正数，尾数是1000100　10000000　00000000，因此是(1.10001001)2，指数位为(10000101)2，指数位的处理方法是将指数位视为无符号整数，然后减去+127偏移量，得到的就是指数，这里(10000101)2=133，　133-127=6，所以26×(1.10001001)2=(1100010.01)2=(98.25)10

  • 第16题：

    现在有负无限值双精度浮点数x和负有限值单精度浮点数y，以下关于x%y的说法中，______是正确的。

    A．NaN

    B．负无限双精度浮点数

    C．负有限双精度浮点数

    D．负无限单精度浮点数


    正确答案：A

  • 第17题：

    十进制数101的二进制代码为（）。


    正确答案:1100101

  • 第18题：

    已知内存中32位位模式为“1  1000 0001   1110 0000 0000 0000 0000 000”当该位模式表示的是单精度浮点数，假定浮点数编码采用Excess-127表示指数部分，通过计算解码出该浮点数对应的十进制数值。写出计算步骤。


    正确答案: 符号为负号    位移量=129-127=2  111.1000 0000 0000 0000 0000 0
    该数绝对值是7.5     该数是-7.5

  • 第19题：

    按IEEE754标准，一个浮点数由（）、（）、（）三个域组成。


    正确答案:符号位S；阶码E；尾数M

  • 第20题：

    将下列单精度浮点数转换为十进制数。  （1）0 10000000 1100000 00000000 00000000  （2）1 01111111 0000000 00000000 00000000  （3）0 10000000 1001000 00000000 00000000


    正确答案:（1）1.11×21=11.1B=+3.5D
    （2）-1.0×20=-1B=-1D
    （3）1.1001×21=11.001B=+3.125D

  • 第21题：

    若IEEE754单精度格式为（-1）s×（1.M）×2E-127，则十进制数-3/4表示成754标准的十六进制数据为（）。

    • A、3F200000H
    • B、BF200000H
    • C、3F400000H
    • D、BF400000H

    正确答案:D

  • 第22题：

    单选题
    在IEEE754标准中，浮点数的表示采用单精度格式是（）位。
    A

    64

    B

    32

    C

    16

    D

    128


    正确答案： C
    解析： 暂无解析

  • 第23题：

    单选题
    已知IEEE 754单精度浮点数十六进制值为42E48000，那它的十进制为（　　）。
    A

    114.25

    B

    57.125

    C

    50.25

    D

    28.5625


    正确答案： A
    解析：
    将此十六进制表示浮点数表示为二进制为0 10000101 110 0100 1000 0000 0000 0000，其中阶码为133，换成原码为6，所以此数为1.11001001×26＝1110010.01(B)，换成十进制为114.25。

相关内容