从2、3、5三个数中，任取两个数，可组成( )个真分数．

题目
从2、3、5三个数中，任取两个数，可组成( )个真分数．

相似考题

1.从1，2，3，……，10共十个数字中任取一个，然后放回，先后取出5个数字，则所得5个数字全不相同的事件的概率等于( )。A．0.3024B．0.0302C．0.2561D．0.0285

2.从1，2，3，4，5中任取3个数，组成的没有重复数字的三位数共有 （ ）A.40个B.80个C.30个D.60个

3.从1、2、3、4、5、6、7、8、9、10这10个数字中，任取5个数相加的和与其余5个数相加的和相乘，能得到多少个不同的乘积?（ ）A．13B．14C． 18D． 20

4.从2,4,8,16这4个数中任取两个不同的数相乘,可以得到________个有别于已知数的不同乘积。A．2B．3C．5D．7

更多“从2、3、5三个数中，任取两个数，可组成( )个真分数．”相关问题

  • 第1题：

    从1,2,…,10这十个自然数中任取三个数，则这三个数中最大的为3的概率是1/120。()


    正确答案:对

  • 第2题：

    从1，2，3，4，5，9中任取不同的两个数字，分别作为对数的真数和底数，能得到（ ）个不同的对

    A．16

    B．17

    C．18

    D．20


    正确答案：B
    首先l不能为底，1的对数是O；以2，3，4，5，9中任取2个数，B

  • 第3题：

    从1,3,5,7,9中任取两个数组成一组数，写出其中两数之和小于10的所有数组。


    1与3  ，1与5  ，1与7  ，3与5


  • 第4题：

    从0、3、5、7、11五个数中任取两个数相乘，可以得到（ ）个不相等的积。

    A．5

    B．4

    C．6

    D．7


    正确答案：D
    因为0和任何数相乘都等于0，所以其只算是一种乘积，C(2/4)＝6，所以可以得到7个不同的乘积。

  • 第5题：

    从0，1，2，3，4，5这六个数字中任取两个奇数和两个偶数，组成没有重复数字的四位数的个数为

    (A)300 (B)216 (C) 180 (D)162


    正确答案：C

  • 第6题：

    从1、2、3、4中任取3个数组成没有重复的三位数的偶数，取法种数为（）。

    A.13
    B.12
    C.10
    D.11

    答案：B
    解析：
    题干要求组成没有重复数字的三位数的偶数，只有尾数是2或4两种情况。当尾数是2时，有2x3=6(种）；当尾数是4时，有2x3=6(种），所以共有6+6=12(种），故本题答案为B。

  • 第7题：

    从1，2，3，4，5，6，7中任取2个数字，分别作为一个分数的分子和分母，则在所得分数中不相同的最简真分数一共有多少个？

    A.14
    B.17
    C.18
    D.21

    答案：B
    解析：
    根据题意，当分母为2时，分子可为1；分母为3时，分子可为1、2；分母为4时，分子可为1、3；分母为5时，分子可为1、2、3、4；分母为6时，分子可为1、5；分母为7时，分子可为1、2、3、4、5、6。因此，满足条件的最简真分数共有1+2+2+4+2+6=17个。

  • 第8题：

    从0,1,2,3,4,5中任取3个数字,组成能被3整除的无重复数字的3位数有（ ）个

    A.18
    B.24
    C.36
    D.40
    E.96

    答案：D
    解析：

  • 第9题：

    从1、2、3、4中任取3个数组成没有重复的三位数且必须为偶数，则取法种数为（ ）。
    A. 13 B. 12 C. 10 D. 11


    答案：B
    解析：
    题干要求组成没有重复数字的三位数且是偶数，只有尾数是2或4两种情况。当尾数是2时，有2X3 = 6（种）；当尾数是4时，有2X3 = 6（种），所以共有6 + 6 = 12（种），故本题答案为B。

  • 第10题：

    如果从1，2，…，10这十个自然数中任取三个数，则这三个数中最大的为3的概率是1/120


    正确答案:正确

  • 第11题：

    从1，2，3，4，5，6，7中任取2个数字，分别作为一个分数的分子和分母，则在所得分数中不相同的最简单真分数一共有多少个？

    • A、14 
    • B、17 
    • C、18 
    • D、21

    正确答案:B

  • 第12题：

    问答题
    35.从1，2．3，4，5中任取3个数字，则这3个数字中不含1的概率为

    正确答案：
    解析：

  • 第13题：

    从n个数字中有返回地任取r个数(r <= n,且n个数字互不相同),则取到的r个数字中有重复数字的概率为( )。


    参考答案：

  • 第14题：

    从3、5、7、11四个数中任取两个数相乘，可以得到多少个不相等的积?

    A．5

    B．4

    C．6

    D．7


    正确答案：C
    [答案] C。解析：四个数两两互质，所以只要选取的乘数不同所得的积就不相同，C42=6，选C。

  • 第15题：

    从l、2、3、4、5、6、7、8、9、10这l0个数字中， 任取5个数相加的和与其余5个数相加的和相乘，能得到多少个不同的乘积?( )

    A 1 3

    B．1 4

    C．18

    D．20


    正确答案：A
    15．A【解析】从整体考虑， 分两组和不变：1+2+3+4+5+6+7+8+9+10=55。从极端考虑分成最小和最大的两组为(1+2+3+4+5)+(6+7+8+9+10)=15+40=55， 最接近的两组为27+28，所以共有27—15+1=13个不同的积。

  • 第16题：

    从1、2、3、4、5、6、7、8、9、10这10个数中，任取5个数相加的和与其余5个数相加的和相乘，能得到多少个不l司的乘积？（ ）

    A．13

    B．14

    C．18

    D．20


    正确答案：A
    从整体考虑分两组，和不变：1+2+3+4+5+6+7+8+9+10=55。从极端考虑分成最小和最大的两组为(1+2+3+4+5)+(6+7+8+9+10)=15+40=55，最接近的两组为27+28，所以共有27-15+1=13个不同的积。

  • 第17题：

    从1，2，3，4，5，6，7这七个数字中任取两个奇数和两个偶数，组成没有重复数字的四位数，其中奇数的个数为

    (A)432 (B)288 (C) 216 (D)108


    正确答案：C

  • 第18题：

    从3、5、7、11四个数中任取两个数相乘，可以得到多少个不相等的积：
    A 5
    B 4
    C 6
    D 7


    答案：C
    解析：

  • 第19题：

    从1、2、3、…、n中，任取57个数，使这57个数必有两个数的差为13，则n的最大值为多少？( )

    A.106
    B.107
    C.108
    D.109

    答案：C
    解析：
    根据两数之差不能为13，构造(1、14、27、40、…)、(2、15、28、41、…)、(3、16、29、42…)、…、(13、26、39、…)。显然每个括号中均不能取连续的两个数，现要求任取57个数必有两数差为13时，n的最大值，那考虑取57个可能没有两数之差为13时，凡的最小值，显然每组数中取第1、3、5、7、…个数可使n最小，相当于每26个数取前13个数，那么要取57个数，57÷13-4……5，n最小为26×4+5=109.即n为109时就能满足取57个数且可能没有两数之差为13的情况，当n为108时，必然有两个数之差为13，所以n的最大值为108，

  • 第20题：

    从1到10这10个整数中任取3个数，恰有1个质数的概率是（ ）.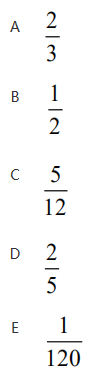


    答案：B
    解析：

  • 第21题：

    从1，2，…，10共十个数字中任取一个，然后放回，先后取出5个数字，则所得5个数字全不相同的事件的概率等于（）


    正确答案:0.3024

  • 第22题：

    从1，2，3，4，5，6，7中任取2个数字，分别作为一个分数的分子和分母，则在所得分数中不相同的最简真分数一共有多少个（）

    • A、14个
    • B、17个
    • C、18个
    • D、21个

    正确答案:B

  • 第23题：

    从数字1，2，…，10中有放回地任取4个数字，则数字10恰好出现两次的概率为（）


    正确答案:0.0486

相关内容