已知等差数列前n项和 (Ⅰ)求这个数列的逋项公式; (II)求数列第六项到第十项的和.
题目
已知等差数列前n项和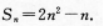
(Ⅰ)求这个数列的逋项公式;
(II)求数列第六项到第十项的和.
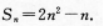
(Ⅰ)求这个数列的逋项公式;
(II)求数列第六项到第十项的和.
相似考题
参考答案和解析
答案:
解析:

更多“已知等差数列前n项和 (Ⅰ)求这个数列的逋项公式; (II)求数列第六项到第十项的和.”相关问题
-
第1题:
一个等差数列,它的开始四项之和为70,最后四项之和为10,所有项的和为640,则这个数列一共有( )项。
A、 56 B、 60 C、 64 D、 72
因为前四项之和为40,最后四项之和为80 所以a1+an=(40+80)/4=30 Sn=n(a1+an)/2=30n/2=210 n=14
-
第2题:
设Sn为等差数列{an}的前n项和,若S3=3,S6=24,则a9= 。
正确答案:
15 -
第3题:
已知等比数列{an}的各项都是正数,且a1+a3=10,a2+a3=6.
(I)求{an}的通项公式;
(II)求{an)的前5项和.答案:解析:
-
第4题:
已知一个等差数列的第五项等于10,前三项的和等于3,那么这个等差数列的公差为( )A.3
B.1
C.-1
D.-3答案:A解析: -
第5题:
等差数列前n项和为210,其中前4项和为40,后4项的和为80,则n的值为( )A.10
B.12
C.14
D.16
E.18答案:C解析:
-
第6题:
已知一等差数列a1,21,a3,31,…,an,…,若an=516,则该数列前n项的平均数是( )A.266 B.258 C.255 D.212答案:A解析:由等差数列的第2项和第4项可求出其公差d==5,则首项a1=21-5=16。又已知an=516,根据等差数列求和公式Sn==平均数×n,可得前n项的平均数为=266。 -
第7题:
—个等差数列有2n —1项,所有偶数项的和为40,所有奇数项的和为50,那么该数列共有 ( )项。
A. 7 B. 8 C. 9 D. 10答案:C解析: -
第8题:
案例:
在等差数列的习题课教学中,教师布置了这样一个问题:等差数列前10项和为100,前100项和为10,求前110项的和。
两位学生的解法如下:
学生甲:设等差数列的首项为a1,公差为d,则

针对上述解法,一些学生提出了自己的想法。
(1)请分析学生甲和学生乙解法各自的特点,并解释学生乙设的理由。(12分)
(2)请验证(*)中结论是否成立。(8分)答案:解析:
-
第9题:
已知数列{%}的前n项和是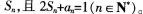
(1)求证:数列{an}是等比数列:
(2)记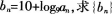 的前n项和Tn的最大值及相应的n值。 答案:解析:
的前n项和Tn的最大值及相应的n值。 答案:解析:
-
第10题:
已知数列{an}满足a1=2,an+1=3an+2(n∈N*),
(1)求数列{an}的通项公式;
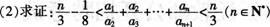 答案:解析:
答案:解析:

-
第11题:
已知数列{an}的前n项和是Sn,且2Sn+an=1(n∈N*)。
(1)求证:数列{an}是等比数列;
(2)记bn=10+log9an,求{bn}的前n项和Tn的最大值及相应的n值。答案:解析: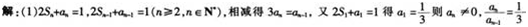
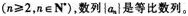
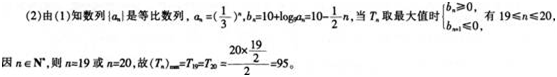
-
第12题:
单选题“斐波那契数列”在求通项公式时,没有用到的知识是:()。A一元二次方程求根公式
B求极限
C等比数列通项公式
D二元一次方程组解法
正确答案: A解析: 暂无解析 -
第13题:
一个等差数列,它的开始四项之和为70,最后四项之和为10,所有项的和为640,则这个数列一共有( )项。
A、 56
B、 60
C、 64
D、 72
正确答案:C
C 解析:由等差数列的性质可知,等差数列的和为项数乘以平均数。本题中,由前四项和后四项的和,可求出平均数为(70+10)÷8=10,因此项数为 640÷10=64。故本题正确答案为C。 -
第14题:
已知等差数列{an}中,a1=21,Sn是它的前n项之和,S7=S15。
(1)求Sn;
(2)这个数列的前多少项之和最大 求出最大值。答案:解析:(1)设等差数列的公差为d,由题意可得:
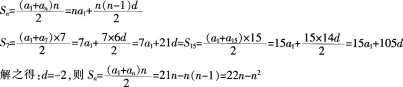
(2)Sn=22n-n2=-(n-11)2+121,当n=11时,数列之和最大,最大值为121。 -
第15题:
已知等比数列{an}的各项都是正数,且a1+a3=10,a2+a3=6.
(Ⅰ)求{an}的通项公式;
(Ⅱ)求{an}的前5项和.答案:解析:解:(Ⅰ)设(an)的公比为q,由已知得
-
第16题:
已知数列{an}中,Sn是它的前n项和,并且Sn+1=4an+2,a1=1.
(Ⅰ)设bn=an+1-2an,求证:数列{bn)是等比数列;
(Ⅱ)设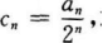 求证:数列{cn}是等差数列;
求证:数列{cn}是等差数列;
(Ⅲ)求数列{an}的通项公式及前n项和.答案:解析:
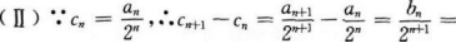


-
第17题:
已知数列{an}的通项公式为an=2n,数列{bn}的通项公式为bn=3n+2.若数列{an}和{bn}的公共项顺序组成数列{cn},则数列{cn}的前3项之和为( )A.248
B.168
C.128
D.19
E.以上选项均不正确答案:B解析:
-
第18题:
高中数学《等比数列前n项和》
一、考题回顾
题目来源:5月19日 上午 重庆市 面试考题
试讲题目
1.题目:等比数列前n项和
2.内容:

3.基本要求:
(1)引导学生应用等比数列前n项和;
(2)试讲10分钟;
(3)合理设计板书;
(4)要有适当的提问互动环节。
答辩题目
1.等差数列的前n项和公式是什么?
2.怎样才能设计好授课板书呢?你能给出几点建议吗?答案:解析:二、考题解析
【教学过程】
(一)引入新课
复习等差数列前n项和公式。提问:等比数列前n项和怎么求呢?有没有相应的公式呢?
引出课题。
(二)探索新知


-
第19题:
已知数列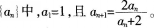 (1)求证:数列
(1)求证:数列 是等差数列:
是等差数列:
(2)求数列 的通项公式。 答案:解析:
的通项公式。 答案:解析: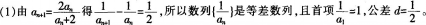 (2)数列
(2)数列 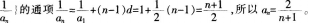
-
第20题:
案例:
在等差数列的习题课教学中,教师布置了这样一个问题:等差数列前10项和为100,前100项和为10,求前110项的和。
两位学生的解法如下:
学生甲:设等差数列的首项为a1,公差为d,则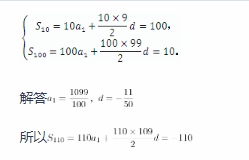
学生乙:设等差数列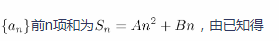
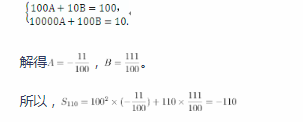
针对上述解法,一些学生提出了自己的想法。
(1)请分析学生甲和学生乙解法各自的特点,并解释学生乙设的理由。(12分)
(2)请验证(*)中结论是否成立。答案:解析:本题主要从“等差数列”相关知识入手,考查等差数列的相关概念、等差数列的通项公式、求和公式等基层知识,教学工作的基本环节,常用的教学方法,以及课堂导入技巧等基本知识与技能。
-
第21题:
(10分)已知数列{an}满足a1=3,an+1= an +2n,
(1)求{ an }的通项公式an;
(2)若bn=n an,求数列{bn}的前n项和sn。答案:解析:
-
第22题:
(10分)已知数列{an}的前n项和Sn=2n+1-k(其中k为常数):
(1)求数列{ an }的通项公式;(4分)
(2)若a1=2,求数列{n an }的前n项和Tn。(6分)答案:解析:
-
第23题:
有一等差数列,共8项。已知公差为2,第2项为4,求第三项的值。答案中含有的信息量是()。
- A、log1
- B、log2
- C、log8
- D、log(1/8)
正确答案:A
