用迭代法解线性方程组时,迭代法是否收敛与初始向量的选择、系数矩阵及其演变方式有关,与常数项无关。()
题目
用迭代法解线性方程组时,迭代法是否收敛与初始向量的选择、系数矩阵及其演变方式有关,与常数项无关。()
相似考题
更多“用迭代法解线性方程组时,迭代法是否收敛与初始向量的选择、系数矩阵及其演变方式有关,与常数项无关。()”相关问题
-
第1题:
使用迭代法的关键问题是其收敛性与收敛速度,收敛性与迭代初值的选取有关。()
参考答案:错误
-
第2题:
解非线性方程f(x)=0的牛顿迭代法在重根附近()A、线性收敛
B、三次收敛
C、平方收敛
D、不收敛
参考答案:A
-
第3题:
运用牛顿-拉夫逊迭代法时应使选择的初值()。A、不等于精确解
B、远大于精确解
C、接近精确解
D、远小于精确解
正确答案:C
-
第4题:
设A为m×n阶矩阵,则齐次线性方程组AX=0只有零解的充分必要条件是(64)。
A.A的列向量组线性无关
B.A的列向量组线性相关
C.A的行向量组线性无关
D.A的行向量组线性相关
A.A的列向量组线性无关
B.A的列向量组线性相关
C.A的行向量组线性无关
D.A的行向量组线性相关
正确答案:A
解析:齐次线性方程组AX=0只有零解的充分必要条件是A的列向量组线性无关 -
第5题:
设A为m×n矩阵,则齐次线性方程组Ax=0有非零解的充分必要条件是( )。A、矩阵A的任意两个列向量线性相关
B、矩阵A的任意两个列向量线性无关
C、矩阵A的任一列向量是其余列向量的线性组合
D、矩阵A必有一个列向量是其余列向量的线性组合答案:D解析:
-
第6题:
已知非齐次线性方程组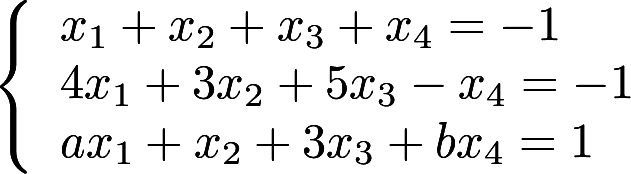 有3个线性无关的解. (Ⅰ)证明方程组系数矩阵A的秩
有3个线性无关的解. (Ⅰ)证明方程组系数矩阵A的秩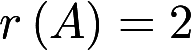 ; (Ⅱ)求
; (Ⅱ)求 的值及方程组的通解答案:解析:
的值及方程组的通解答案:解析:

-
第7题:
设Ax=b,其中A对称正定,问解此方程组的雅可比迭代法是否一定收敛?
正确答案:A对称正定,Jacobi迭代法不一定收敛。 -
第8题:
对于迭代法xn+1=φ(x),(n=0,1,...)初始近似x0,当|φ′(x0)|<1时为什么还不能断定迭代法收敛?
正确答案: 迭代法是否收敛一定要按收敛定理的条件判断,定理6.1是全局收敛性,需要在包含x0是全局收敛性,需要在包含的区间[a,b]上证明a≤φ(x)≤b且才能说明由x0出是迭代法xn+1=φ(x)收敛。
如果用局部收敛定理6.2,则要知道不动点为x*才可由φ′(x0)<1还不能说明迭代法收敛。 -
第9题:
判断题在数值分析中,迭代解法主要包括:Jacobi迭代法、Gauss-Serdel迭代法、超松弛迭代法和两步迭代法。A对
B错
正确答案: 对解析: 暂无解析 -
第10题:
填空题解非线性方程f(x)=0的牛顿迭代法具有()收敛。正确答案: 局部平方解析: 暂无解析 -
第11题:
问答题对于迭代法xn+1=φ(x),(n=0,1,...)初始近似x0,当|φ′(x0)|<1时为什么还不能断定迭代法收敛?正确答案: 迭代法是否收敛一定要按收敛定理的条件判断,定理6.1是全局收敛性,需要在包含x0是全局收敛性,需要在包含的区间[a,b]上证明a≤φ(x)≤b且才能说明由x0出是迭代法xn+1=φ(x)收敛。
如果用局部收敛定理6.2,则要知道不动点为x*才可由φ′(x0)<1还不能说明迭代法收敛。解析: 暂无解析 -
第12题:
问答题设Ax=b,其中A对称正定,问解此方程组的雅可比迭代法是否一定收敛?正确答案: A对称正定,Jacobi迭代法不一定收敛。解析: 暂无解析 -
第13题:
线性方程组的数值解法有哪几类
A、直接法
B、迭代法
C、间接法
D、递归法
参考答案:AB
-
第14题:
线性方程组的数值解法有:直接法和迭代法。()此题为判断题(对,错)。
正确答案:正确
-
第15题:
线性方程组的解法大致可以分为()
A、直接法和间接法
B、直接法和替代法
C、直接法和迭代法
D、间接法和迭代法
参考答案:C
-
第16题:
设n阶矩阵A的伴随矩阵A^*≠0,若ζ1,ζ2,ζ3,ζ4是非齐次线性方程组Ax=b的互不相等的解,则对应的齐次线性方程组Ax=0的基础解系A.不存在.
B.仅含一个非零解向量.
C.含有两个线性无关的解向量.
D.含有三个线性无关的解向量.答案:B解析:
-
第17题:
设3阶实对称矩阵A的各行元素之和都为3,向量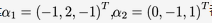 都是齐次线性方程组AX=0的解.① 求A的特征值和特征向量.② 求作正交矩阵Q和对角矩阵
都是齐次线性方程组AX=0的解.① 求A的特征值和特征向量.② 求作正交矩阵Q和对角矩阵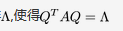 答案:解析:
答案:解析:
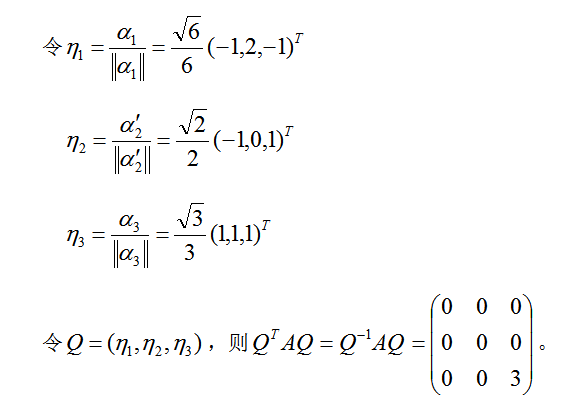
-
第18题:
在数值分析中,迭代解法主要包括:Jacobi迭代法、Gauss-Serdel迭代法、超松弛迭代法和两步迭代法。
正确答案:正确 -
第19题:
工程路线问题也称为最短路问题,根据问题的不同分为定步数问题和不定步数问题;对不定步数问题,用迭代法求解,有()迭代法和()迭代法两种方法。
正确答案:函数;策略 -
第20题:
解非线性方程f(x)=0的牛顿迭代法具有()收敛。
正确答案:局部平方 -
第21题:
单选题设A为m×n矩阵,则齐次线性方程组Ax=0有非零解的充分必要条件是( )。[2017年真题]A矩阵A的任意两个列向量线性相关
B矩阵A的任意两个列向量线性无关
C矩阵A的任一列向量是其余列向量的线性组合
D矩阵A必有一个列向量是其余列向量的线性组合
正确答案: D解析:
线性方程组Ax=0有非零解⇔|A|=0⇔r(A)<n,矩阵A的列向量线性相关,所以矩阵A必有一个列向量是其余列向量的线性组合。 -
第22题:
单选题设A为m×n矩阵,齐次线性方程组AX(→)=0(→)仅有零解的充分条件是( )。AA的列向量组线性无关
BA的列向量组线性相关
CA的行向量组线性无关
DA的行向量组线性相关
正确答案: C解析:
因为AX=0仅有零解的充分必要条件是A的秩r(A)=n,所以A的列向量组线性无关是AX=0仅有零解的充分条件。 -
第23题:
单选题对于系数为正定对称矩阵的线性方程组,其最佳求解方法为( )A追赶法
B平方根法
C迭代法
D高斯主元消去法)
正确答案: B解析: 暂无解析 -
第24题:
单选题n元线性方程组AX(→)=b(→)有唯一解的充要条件为( )。AA为方阵且|A|≠0
B导出组AX=0仅有零解
C秩(A)=n
D系数矩阵A的列向量组线性无关,且常数向量b与A的列向量组线性相关
正确答案: C解析:
A项,系数矩阵A不一定是方阵;B项,导出组只有零解,方程组AX=b不一定有解;C项,当r(A)=n时,不一定有r(A)=r(A)=n;D项,b可由A的列向量组线性表示,则方程组AX=b有唯一解。
