任意两个非齐次线性方程组的解的差事谁的解？
题目
任意两个非齐次线性方程组的解的差事谁的解？
相似考题
更多“任意两个非齐次线性方程组的解的差事谁的解？”相关问题
-
第1题：
非齐次线性方程组任意两个解之差为对应系数的齐次线性方程组的解。()
参考答案：正确
-
第2题：
若A是m×n矩阵，且m≠n，则当R（A）=n时，非齐次线性方程组AX=b，有唯一解答案：错解析： -
第3题：
设n阶矩阵A的伴随矩阵A^*≠0，若ζ1，ζ2，ζ3，ζ4是非齐次线性方程组Ax=b的互不相等的解，则对应的齐次线性方程组Ax=0的基础解系A.不存在.
B.仅含一个非零解向量.
C.含有两个线性无关的解向量.
D.含有三个线性无关的解向量.答案：B解析：
-
第4题：
解齐次线性方程组：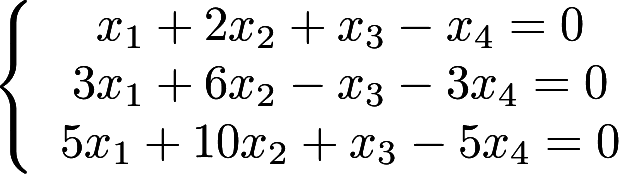
答案：解析：
-
第5题：
设有齐次线性方程组
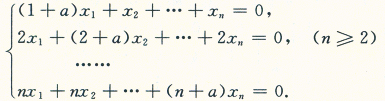
试问a为何值时，该方程组有非零解，并求其通解.答案：解析：
-
第6题：
已知齐次线性方程组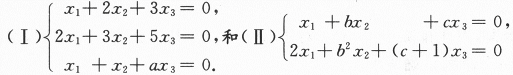
同解，求a，b，c的值.答案：解析：
-
第7题：
求出一个齐次线性方程组，使它的基础解系由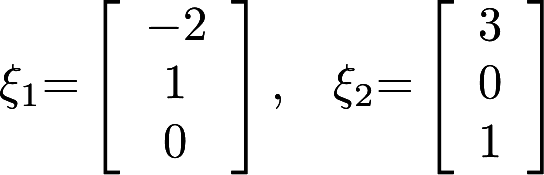
向量组成答案：解析：
-
第8题：
问：齐次线性方程组
有非零解时，a,b必须满足什么条件？答案：解析：
-
第9题：
设非齐次线性方程组( I )的导出方程组为(II)，则()。A.当(I )只有唯一 解时，(II)只有零解
B. (I )有解的充分必要条件是(II)有解
C.当(I )有非零解时，(II)有无穷多解
D.当(I)有非零解时，(I )有无穷多解答案：A解析： -
第10题：
齐次线性方程组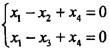
的基础解系为（ ）。
答案：C解析：提示：求解所给方程组，得基础解系α1=（1,1,1,0）T,α2=（-1,0,0,1）T,故选C。也可将选项代入方程验证。 -
第11题：
已知非齐次线性方程组有无限多个解，则t等于（）．
- A、-1
- B、1
- C、4
- D、-1或4
正确答案:C -
第12题：
单选题设A是4×6矩阵，则齐次线性方程组AX=0解的情况是（）。A无解
B只有零解
C有非零解
D不一定
正确答案： A解析： AX=0有非零解的充要条件是R（A）＜6，而4×6矩阵的秩R（A）≤4，故AX=0有非零解，故选（C）。 -
第13题：
齐次线性方程组AX=0若有两个不同的解，它就有无穷多个解答案：对解析： -
第14题：
设A是m×n阶矩阵，Ax=0是非齐次线性方程组Ax=b所对应的齐次线性方程组，则下列结论正确的是( )。A.若Ax=0仅有零解，则Ax=b有惟一解
B.若Ax=0有非零解，则Ax=b有无穷多个解
C.若Ax=b有无穷多个解，则Ax=0仅有零解
D.若Ax=b有无穷多个解，则Ax=0有非零解答案：D解析：
-
第15题：
求齐次线性方程组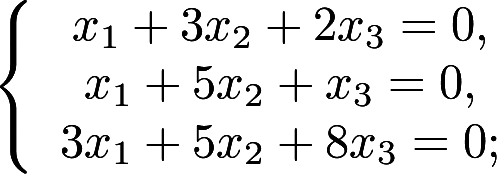
的基础解系答案：解析：
-
第16题：
解非齐次线性方程组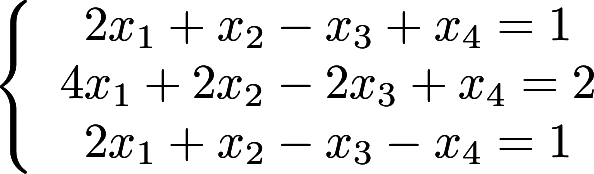
答案：解析：
-
第17题：
问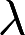
取何值时 非齐次线性方程组
， (1)有唯一解 (2)无解 (3)有无穷多个解，并在无穷多个解时，求方程组的通解答案：解析：
-
第18题：
设(Ⅰ)和(Ⅱ)是两个四元齐次线性方程组,(Ⅰ)为
，(Ⅱ)有一个基础解系(0,1,1,0)T,(-1,2,2,1)T．求(Ⅰ)和(Ⅱ)的全部公共解答案：解析：
-
第19题：
设有齐次线性方程组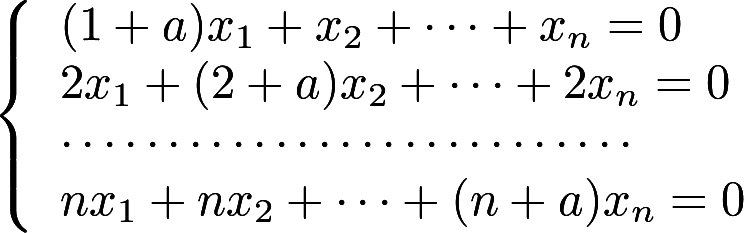
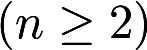.试问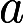
取何值时，该方程组有非零解，并求出其通解答案：解析：
-
第20题：
已知齐次线性方程组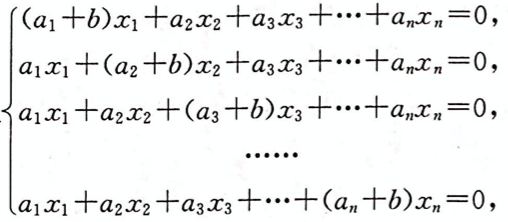
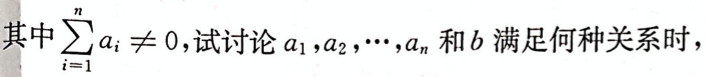（1）方程组仅有零解；（2）方程组有非零解，在有非零解时，求此方程组的一个基础解系.答案：解析：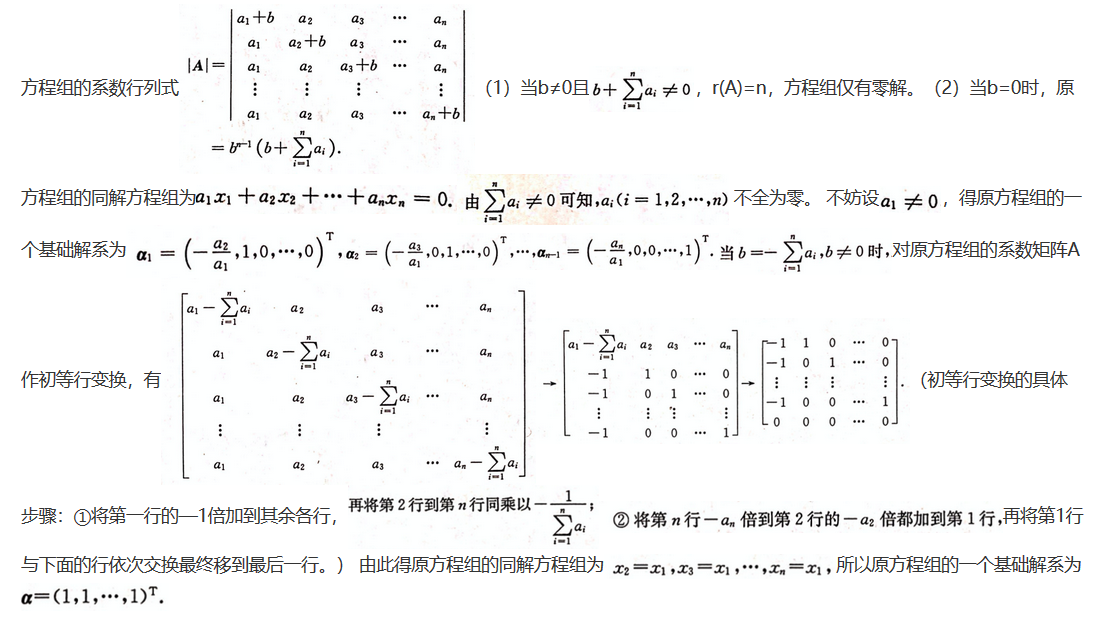
-
第21题：
求齐次线性方程组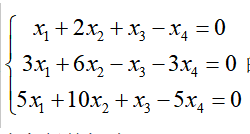
的全部解（要求用基础解系表示）。答案：解析：解：本题考查齐次线性方程组的解法。
-
第22题：
设A为矩阵，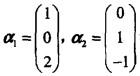
都是齐次线性方程组Ax=0的解，则矩阵A为( )。
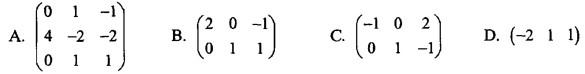答案：D解析：提示：由于
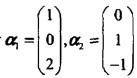线性无关，故R(A)= 1，显然选项A中矩阵秩为3,选项B和C中矩阵秩都为2。 -
第23题：
设A是4×6矩阵，则齐次线性方程组AX=0解的情况是（）。
- A、无解
- B、只有零解
- C、有非零解
- D、不一定
正确答案:C -
第24题：
单选题n阶矩阵A的伴随矩阵为A*，齐次线性方程组AX(→)＝0(→)有两个线性无关的解，则（ ）。AA*X＝0的解均是AX＝0的解
BAX＝0的解均是A*X＝0的解
CAX＝0与A*X＝0无非零公共解
DAX＝0与A*X＝0仅有2个非零公共解
正确答案： A解析：
由齐次方程组AX＝0有两个线性无关的解向量，知方程组AX＝0的基础解系所含解向量的个数为n－r（A）≥2，即r（A）≤n－2＜n－1。由矩阵A与其伴随矩阵秩的关系，知r（A*）＝0，即A*＝0。所以任意n维列向量均是方程组A*X＝0的解，故方程组AX＝0的解均是A*X＝0的解。