单选题设谓词P（x）：x是奇数，Q（x）：x是偶数，谓词公式∃x（P（x）∨Q（x））在哪个个体域中为真？（　　）A 自然数B 实数C 复数D A，B，C均成立

题目

单选题

设谓词P（x）：x是奇数，Q（x）：x是偶数，谓词公式∃x（P（x）∨Q（x））在哪个个体域中为真？（　　）

自然数

实数

复数

A，B，C均成立

相似考题

1.已知指针p和q分别指向某单链表中第一个结点和最后一个结点。假设指针x指向另一个单链表中某个结点,则在s所指结点之后插入上述链表应执行的语句为()。A、q->next=x->next;x->next=p;B、s->next=p;q->next=x->next;C、p->next=x->next;x->next=p;D、x->next=q;p->next=x->next;

2.以下4个程序中，不能实现两个实参值进行交换的是 ( )。A．void swap (float *p, float *q) { float *t ,a; t = &a; t = p; *p = *q; *q = *t; } void main () { float x = 8.0;y = 9.0; swap (&x, &y); cout＜＜x＜＜", "＜＜y＜＜B．void swap (float *p, float *q) { float a; a = *p; *p = *q; *q = a; } void main() { float x = 8.0;y = 9.0; swap (&x, &y); cout＜＜x＜＜", "＜＜y＜＜end1;C．void swap (float *p, float *q) { float x; x = *p; *p = *q; *q = x; } void main() { float a,b.; *a = 8.0;*b = 9.0; swap (a, b) ;D．void swap (float &p, float &q) { float a; a = p; p = q; q = a; } void main() { float a = 8.0,b = 9.0; swap (a,b); cout＜＜x＜＜", "＜＜y＜＜

3.已知集合P={x|0 ≤x ≤5,x∈Z},Q={y|y=|x2-1|,x∈P},则P∩Q中元素的个数是( ).(A)3.(B)6.(C)8.(D)9.

4.设 f(x)ϵP[x] ，，则f(x)与q(x)的关系是()A.B.C.D.

更多“单选题设谓词P（x）：x是奇数，Q（x）：x是偶数，谓词公式∃x（P（x）∨Q（x））在哪个个体域中为真？（　　）A 自然数B 实数C 复数D A，B，C均成立”相关问题

第1题：

设有关键码序列(q，g，m，z，a，n，p，x，h)，下面哪一个序列是从上述序列出发建堆的结果?( )
A．a，g，h，m，n，p，q，x，z
B．a，S，m，h，q，n，p，x，z
C．g，m，q，a，n，p，x，h，z
D．h，g，m，p，a，n，q，x，z

正确答案：B
解析：堆的定义是对每个层次的树(子树)都存在双亲节点小于(大于)其子女节点。因此要么是小根堆，要么是大根堆，小根堆堆顶元素肯定是a，大根堆堆顶元素肯定是z，因此首先可以排除C和D选项。对A、B如果是堆，肯定是小根堆。再根据建初堆后，进行筛运算的结果可得应为B。
第2题：

以下程序的运行结果为______。 main() { int x,*p,**q; x=10;p=&x;q=&p; printf("%d\n",**q); }
A．10
B．9
C．8
D．11

正确答案：A
解析：程序中的p指向变量x，q被定义为二级指针，即指向指针的指针，其值为指针p的地址，因此，**q即是x，打印结果为10。
第3题：

设P(x)：x是金子，Q(x)：x闪光，则命题“没有不闪光的金子”形式化为(53)。
A．
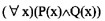
B．
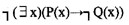
C．
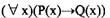
D．

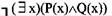正确答案：C
解析：在命题形式化时，如果用全总个体域，则对每一个个体变元的变化范围用特性谓词加以限制。一般地，对于全称量词，特性谓词应以条件式的前件加入：对于存在量词，特性谓词应以合取式的合取项加入。对于复杂的命题，在翻译时尽量按命题的语序进行翻译，然后可以利用逻辑等价变换进行化简。本题既测验翻译又测验等价变换。试题求解过程如下：［*］“没有不闪光的金子”按语序可形式化：［*］因此，“没有不闪光的金子”也可翻译为：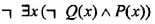
第4题：

正态分布计算所依据的重要性质为（）。
A.设X~N(μ,σ2),则μ= (X-μ)/σ~N(0, 1)
B.设X~N(μ,σ2),则对任意实数a、b有P(XC.设X~N(μ,σ2),则对任意实数a、b有P(X>a) =1-Φ[(a-μ)/σ]
D.设X~N(μ,σ2),则对任意实数a、b有P(a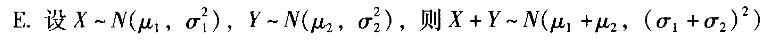

答案：A,B,C,D
解析：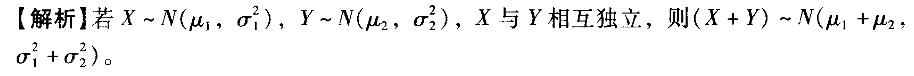
第5题：

设随机变量X~N(0，σ2)，则对于任何实数λ，都有：

A. P(X≤λ)=P(X≥λ)
B.P(X≥λ)=P(X≤-λ)
C.X-λ~N(λ,σ2-λ2)
D.λX~N(0,λσ2)

答案：B
解析：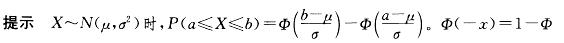

(x)，Y=aX+b~N(au+b,a2σ2)，或利用u=0时概率密度f(x)曲线的对称性，概率(积分值)与曲边梯形面积对应判断。
第6题：

设随机变量X～F(m,m),令p=P(X≤1),q=P(X≥1),则().

A.pB.p>q
C.p=q
D.p,q的大小与自由度m有关

答案：C
解析：
因为X～F(m，m)，所以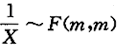，于是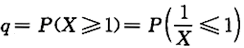，故p=q，选(C).
第7题：

两个本原多项式g（x）和f（x），令h（x）=g（x）f（x）记作Cs，若h（x）不是本原多项式，则存在p当满足什么条件时使得p|Cs（s=0，1…）成立？（）
- A、p是奇数
- B、p是偶数
- C、p是合数
- D、p是素数
正确答案:D
第8题：

已知p：方程x²+mx+1=0有两个不等负实根。q：方程4x²+4（m-2）x+1=0无实根。若p或q为真，p且q为假。求实数m的取值范围。

正确答案: 因为p或q为真，p且q为假，则必然p与q中有一真一假。分两种情况：p为真，q为假；q为真，p为假。
（1）若p为真，则q为假。
p为真，方程x²+mx+1=0有两个不等负实根成立，即△=m²-4>0，x+x=m<0，解得：m>2或m<-2，m>0。综上两式得到：m>2。
q为假，方程4x²+4（m-2）x+1=0无实根不成立，即有实数根，△=16（m-2）²-16≥0，所以m≥3或m≤1。
取交集得到，m≥3：
（2）若q为真，则p为假。
q为真，即方程4x²+4（m-2）x+1=0无实根成立，即△=16（m-2）²-16<0，所以1p为假，方程x²+mx+1=0有两个不等负实根不成立，即①无实根或有两个相等实根，△=m²-4≤0，或②有两个不等正实根，△=m²-4>0，x+x=-m>0。解得，①-2≤m≤2或②m<-2，所以m≤2。
取交集得到：1综上所述m≥3或1
第9题：

若p/q是f（x）的根，其中（p，q）=1，则f（x）=（px-q）g（x），当x=1时，f（1）/（p-q）是什么？（）
- A、复数
- B、无理数
- C、小数
- D、整数
正确答案:D
第10题：

单选题
在计算管网效率中，通常可按简易的管网效率公式计算。公式（）可计算当管网漏失量为0时的管网效率。
A
[△pQ/3.6P]x100%
B
[p/（p+△p）]x（Q△Q）
C
p/（p+△p）x100%
D
Q/Q△Qx100%

正确答案： D
解析：暂无解析
第11题：

单选题
设谓词P（x）：x是奇数，Q（x）：x是偶数，谓词公式∃x（P（x）∨Q（x））在哪个个体域中为真？（　　）
A
自然数
B
实数
C
复数
D
A，B，C均成立

正确答案： C
解析：
∃x（P（x）∨Q（x））的意思是：存在x，x为奇数或x为偶数。显然当x为自然数时，∃x（P（x）∨Q（x））为真，而x为分数、无理数或复数时都为假，故本题选A。
第12题：

单选题
两个本原多项式g（x）和f（x），令h（x）=g（x）f（x）记作Cs，若h（x）不是本原多项式，则存在p当满足什么条件时使得p|Cs（s=0，1…）成立？（）
A
p是奇数
B
p是偶数
C
p是合数
D
p是素数

正确答案： C
解析：暂无解析
第13题：

下列程序的运行结果是______。 main ( ) { int x,*p,**q; x=10; p=&x; q=&p; printf ("%d\n", **q); }
A．10
B．9
C．8
D．11

正确答案：A
第14题：

设R(x)：x是实数。Q(x)：x是有理数。则(52)正确地翻译了命题“并非每个实数都是有理数”。
A．
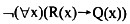
B．
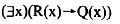
C．
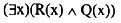
D．

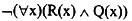正确答案：A
解析：本题考查谓词逻辑的翻译知识。该题的语义是“每个实数都是有理数这种说法是不对的”或者理解为“总存在一些实数不是有理数”。
第15题：

设随机变量X?N(0，σ2)，则对于任何实数λ都有:
(A) P(X≤λ)=P(X≥λ)(B)P(X≥λ)= P(X≤-λ)
(C) X-λ~N(λ，σ2-λ2)(D)λX~N(0，λσ2)

答案：B
解析：
解:选B。
排除错误选项。
X-λ~N(-λ，σ2)，选项C错误。
λX~N(0，λ2σ2)，选项D错误。
第16题：

设X是随机变量，已知P(X≤1)=p，P(X≤2)=q，则P(X≤1，X≤2)等于( ).

A.p+q
B.p-q
C.q-p
D.p

答案：D
解析：
第17题：

7、负载的有功功率为P，无功功率为Q，电压为U，电流为I，确定电抗X大小的关系式是（）。

（A）X＝Q/I ；（B）X=Q/I，；
（C）X=Q /I ；（D）X＝UI /Q。

答案：A
解析：
第18题：

设随机变量X与Y相互独立，已知P(X≤1)=p，P(Y≤1)=q，则P(max(X，Y)≤1)等于( ).

A.p+q
B.pq
C.p
D.q

答案：B
解析：
随机事件{max(X，Y)≤1}={X≤1，y≤1}，因此，由乘法公式得到P(max(X，Y)≤1)=P(X≤1，y≤1)=P(X≤1)P(y≤1)=pq故选B.
第19题：

设X是随机变量，已知P（X≤1）=p，P（X≤2）=q，则P（X≤1，X≤2）等于（）．
- A、p+q
- B、p-q
- C、q-p
- D、p
正确答案:D
第20题：

在计算管网效率中，通常可按简易的管网效率公式计算。公式（）可计算当管网漏失量为0时的管网效率。
- A、[△pQ/3.6P]x100%
- B、[p/（p+△p）]x（Q△Q）
- C、p/（p+△p）x100%
- D、Q/Q△Qx100%
正确答案:C
第21题：

问答题
求出两多项式函数P（x）、Q（x），使得下面等式成立：　　∫[（2x4－1）cosx＋（8x3－x2－1）sinx]dx＝P（x）cosx＋Q（x）sinx＋C

正确答案：
由∫[(2x⁴-1)cosx+(8x³-x²-1)sinx]dx=P(x)cosx+Q(x)sinx+C,两边对x求导,得P′(x)cosx-P(x)sinx+Q′(x)sinx+Q(x)cosx=(2x⁴-1)cosx+(8x³-x²-1)sinx。
等式两边的cosx和sinx项分别相等,则
P′(x)+Q(x)=2x⁴-1①
Q′(x)-P(x)=8x³-x²-1②
将①两边对x求导得P″(x)+Q′(x)=8x³,即
Q′(x)=8x³-P″(x)③
将③代入②整理得
P″(x)+P(x)=x²+1④
假设P(x)=ax²+bx+c,将其代入④得
2a+ax²+bx+c=x²+1
等式两边同次幂的系数应该相等,则a=1,b=0,2a+c=1,解得c=-1。
故P(x)=x²-1,Q(x)=2x⁴-1-P′(x)=2x⁴-1-2x=2x⁴-2x-1。
解析：暂无解析
第22题：

单选题
若p/q是f（x）的根，其中（p，q）=1，则f（x）=（px-q）g（x），当x=1时，f（1）/（p-q）是什么？（）
A
复数
B
无理数
C
小数
D
整数

正确答案： D
解析：暂无解析
第23题：

问答题
已知p：方程x2+mx+1=0有两个不等负实根。q：方程4x2+4（m-2）x+1=0无实根。若p或q为真，p且q为假。求实数m的取值范围。

正确答案：因为p或q为真，p且q为假，则必然p与q中有一真一假。分两种情况：p为真，q为假；q为真，p为假。
（1）若p为真，则q为假。
p为真，方程x²+mx+1=0有两个不等负实根成立，即△=m²-4>0，x+x=m<0，解得：m>2或m<-2，m>0。综上两式得到：m>2。
q为假，方程4x²+4（m-2）x+1=0无实根不成立，即有实数根，△=16（m-2）²-16≥0，所以m≥3或m≤1。
取交集得到，m≥3：
（2）若q为真，则p为假。
q为真，即方程4x²+4（m-2）x+1=0无实根成立，即△=16（m-2）²-16<0，所以1p为假，方程x²+mx+1=0有两个不等负实根不成立，即①无实根或有两个相等实根，△=m²-4≤0，或②有两个不等正实根，△=m²-4>0，x+x=-m>0。解得，①-2≤m≤2或②m<-2，所以m≤2。
取交集得到：1综上所述m≥3或1
解析：暂无解析
第24题：

单选题
设X是随机变量，已知P（X≤1）=p，P（X≤2）=q，则P（X≤1，X≤2）等于（）．
A
p+q
B
p-q
C
q-p
D
p

正确答案： C
解析：暂无解析

单选题设谓词P（x）：x是奇数，Q（x）：x是偶数，谓词公式∃x（P（x）∨Q（x））在哪个个体域中为真？（ ）A 自然数B 实数C 复数D A，B，C均成立

题目

相似考题

更多“单选题设谓词P（x）：x是奇数，Q（x）：x是偶数，谓词公式∃x（P（x）∨Q（x））在哪个个体域中为真？（ ）A 自然数B 实数C 复数D A，B，C均成立”相关问题

相关内容

单选题设谓词P（x）：x是奇数，Q（x）：x是偶数，谓词公式∃x（P（x）∨Q（x））在哪个个体域中为真？（　　）A 自然数B 实数C 复数D A，B，C均成立

更多“单选题设谓词P（x）：x是奇数，Q（x）：x是偶数，谓词公式∃x（P（x）∨Q（x））在哪个个体域中为真？（　　）A 自然数B 实数C 复数D A，B，C均成立”相关问题