已知在Rt△ABC中，∠ACB=90°，AB=4，分别以AC，BC为直径作半圆，面积分别记为S1和S2，则S1+S2的值等于4π。

题目

已知在Rt△ABC中，∠ACB=90°，AB=4，分别以AC，BC为直径作半圆，面积分别记为S1和S2，则S1+S2的值等于4π。

相似考题

1.△ABC中，AB=3，BC=4，则AC边的长满足（ ）。A．AC=5B．AC>1C．AC<7D．1<AC<7

2.在Rt△ABC中，∠ C=90°，BC=5，sinA=0.7，求cosA，tanA的值。

3.在△ABC中，D、E分别是边AB、AC的中点，若BC＝5，则DE的长是（ ）。A．2.5B．5C．10D．15

4.在 △ABC中，∠C=90°，AB=10。（1）∠A=30°，求BC，AC（精确到0.01）；（2）∠A=45°，求BC，AC（精确到0.01）。

参考答案和解析
正确答案:错误
更多“已知在Rt△ABC中，∠ACB=90°，AB=4，分别以AC，BC为直径作半圆，面积分别记为S1和S2，则S1+S2的值等于4π。”相关问题

  • 第1题：

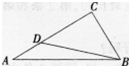
    如图Rt△ABC中，∠ACB=90。，D是AC上靠近A的三等分点，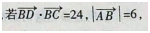




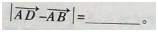
    答案：
    解析：

    解析：

  • 第2题：

    如图，Rt△ABC中，∠ABC=90o,AB=28 cm，以AB为直径的半圆与AC相交，图中的阴影部分①的面积比⑦的面积少28.28 cm2，求BC的长(π取3．14)。


    答案：
    解析：

  • 第3题：

    如图所示，△ABC中DE∥BC，且BO和CO分别是∠ABC和∠ACB的角平分线。已知AB=25.4 cm，BC=24.5 cm，AC=20 cm。问△ADE的周长是多少？

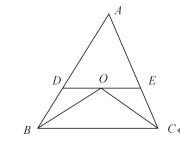
    A．45.4 cm B．45.1 cm C．44.8 cm D．44.5 cm


    答案：A
    解析：
    根据题意可知，DO=BD，OE=EC，则△ADE的周长=AB+AC=45.4 cm。

  • 第4题：

    在△ABC中，已知AB＝5，AC＝3，∠A＝120°，则BC长为



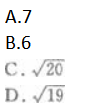    答案：A
    解析：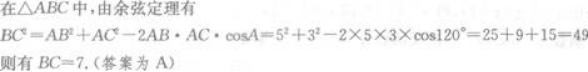

  • 第5题：

    在△ABC中，已知∠A=60°，且BC=4AB，求sinC(精确到0．001)。


    答案：
    解析：
    0．612

  • 第6题：

    如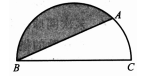，BC是半圆的直径，且BC=4，∠ABC=30°，则图中阴影部分的面积为



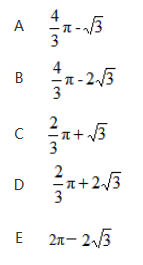    答案：A
    解析：

  • 第7题：

    在三角形ABC，AB=4，AC=6，BC=8，D为BC的中点，则AD=




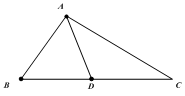
    答案：B
    解析：

  • 第8题：

    如图，在以AB为直径的半圆上取一点C，分别以AC和BC为直径在AABC外作半圆A￡C和BFC。当C点在什么位置时，图中两个弯月形（阴影部分）AEC和BFC的面积和最大？（ ）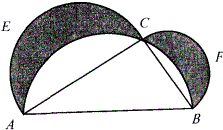


    A. AC大于BC
    B. AC小于BC
    C. AC等于BC
    D.无法得出

    答案：C
    解析：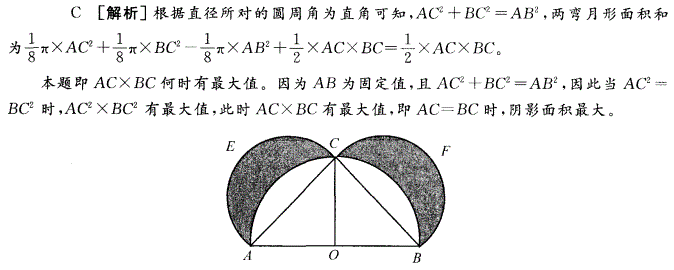

  • 第9题：

    在△ABC中，∠C=90o，AC=8，BC=6，则△ABC的外接圆直径的长为__________ 。


    答案：
    解析：
    10

  • 第10题：

    如图，Rt△ABC中，AB=6，BC=4，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为__________。



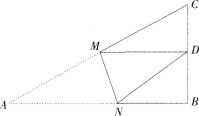    答案：
    解析：

  • 第11题：

    已知Rt△ABC中，斜边BC上的高AD=4，cosB=4/5，则AC=5。


    正确答案:正确

  • 第12题：

    判断题
    已知Rt△ABC中，斜边BC上的高AD=4，cosB=4/5，则AC=5。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第13题：

    锐角三角形ABC中，sinA=√5/5，D为BC边上的点，若△ABD 和△ACD的面积分别为2和4，过D作DE ⊥AB于E，DF⊥AC于F，


    答案：
    解析：

  • 第14题：

    如图，在△ABC中，AC=8，BC=6，∠ACB=90°，动点P以每秒一个单位的速度从点A出发，沿着边AC向点C移动，同时，动点Q以相同的速度从点B出发，沿着边BA向点A移动，设P，Q两点移动时间为t秒(0≤t≤8)。



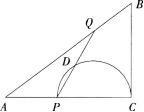
    (1)当t为何值时，△APQ的面积最大 最大值是多少
    (2)以PC为直径的半圆交PQ于点D，是否存在t，使得PD=DQ 若存在，求出t的值，若不存在说明理由。


    答案：
    解析：
    (1)如图，作QH⊥AC，则QH∥BC，



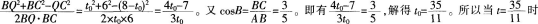
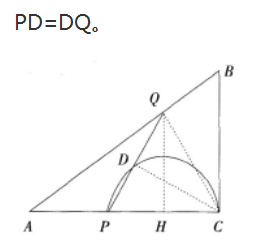
  • 第15题：

    如图，在以为直径的半圆上取一点C，分别以AC和BC为直径在△ABC外作半圆AEC和BFC。当C点在什么位置时，图中两个弯月形（阴影部分）AEC和BFC的面积和最大？（）


    A. AC 大于 BC
    B. AC 小于 BC
    C. AC 等于 BC
    D.无法得出

    答案：C
    解析：

    本题即ACXBC何时有最大值。因为为固定值，且AC2+BC2=AB2，因此当AC2=BC2时， AC2XBC2有最大值，此时ACXBC有最大值，即AC=BC时，阴影面积最大。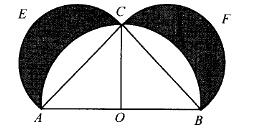

  • 第16题：

    在△ABC中，AB=2，BC=3，B=60°．求AC及△ABC的面积．


    答案：
    解析：
    解：由余弦定理得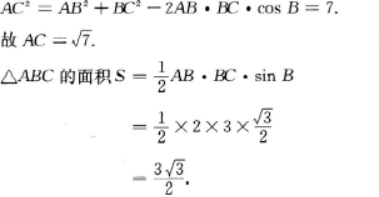

  • 第17题：

    在 ABC中，∠ABC=600，AB=4，BC=6，则AC=（）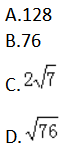


    答案：C
    解析：

  • 第18题：

    已知△ABC和△A'B'C'满足AB:A'B'=AC:AC'=2:3,∠A+∠A'=,则△ABC和△A'B'C'的面积比为（ ）


    答案：E
    解析：
    特值法：假设AB=AC=2,A'B'=A'C'=3,∠A=∠A'=2，S:S'=12*2*2:12*3*3=4:9

  • 第19题：

    如，在直角三角形ABC中，AC=4，BC=3，DE//BC，已知梯形BCDE的面积为3，则DE长为（ ）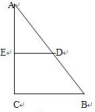



    答案：D
    解析：

  • 第20题：

    已知如图，直角三角形ABC的两直角边AC = 8厘米，BC=6厘米，以AC、BC为边向三角形外分别作正方形ACDE和BCFG，再以AB为边向上作正方形ABMN，其中N点落在DE上，BM交CF于点了，则阴影部分的总面积等于（ ）。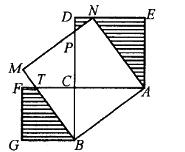

    A. 46平方厘米 B. 38平方厘米
    C. 40平方厘米 D. 48平方厘米


    答案：D
    解析：
    已知ΔABC为直角三角形，AC=8厘米，BC=6厘米，则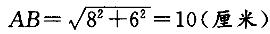。 设四边形ACPN的面积为S1，ΔBCT的面积为S2，四边形CTMP的面积为S3。SACDE + SBGFC = 82 + 62 =102 =SABMN，即S1 + S2 + S阴影=S1 + S2+ S3 + SΔABC ，故S阴影=S3 + SΔABC 。已知四边形ABMN为正方形，则∠BAC + ∠ABC = ∠ABC + ∠CBM，得∠BAC =∠CBM；∠CBM +∠BPM = ∠CBM +∠BTC，则∠BPM =∠BTC。因为AB=BM，所以SΔABT≌SΔBMP（角角边），故S3+SΔBCT=SΔABC +SΔBCT，得S3=SΔABC。故S阴影=2 SΔABC = 2X8X6/2 = 48(平方厘米)。

  • 第21题：

    已知△ABC的三边长AC＝3，BC＝4，AB＝5，P为AB边上任意一点，则CP→ (BA→－BC→)的最大值为(　　)

    A、8
    B、9
    C、12
    D、15

    答案：B
    解析：

  • 第22题：

    在Rt△ABC中，∠C=90°，若cosA=3/5，则tanB的值是( )。

    A.3/5
    B.3/4
    C.4/5
    D.4/3

    答案：B
    解析：
    {图]

  • 第23题：

    判断题
    已知在Rt△ABC中，∠ACB=90°，AB=4，分别以AC，BC为直径作半圆，面积分别记为S1和S2，则S1+S2的值等于4π。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

相关内容