怎样从历史数据中训练出结点之间的条件概率或联合条件概率？

题目

怎样从历史数据中训练出结点之间的条件概率或联合条件概率？

相似考题

1.某轴承厂有甲、乙、丙三个车间，各车间生产的轴承数量分别占全厂的40%、30%、 30%，各车间的次品率分别为3%、4%、5%(正品率分别为97%、96%、95%)。以上叙述如下图所示。在图中，从“厂”结点出发选择三个车间产品的概率分别为0.4、0.3、0.3，从各“车间”结点出发选择“正品”或“次品”的概率如图所示。从“厂”结点出发，到达“正品”(或“次品”)结点，可以有多条路径。例如，路径“厂—甲一次品”表示该厂甲车间生产的次品，其概率P(厂一甲一次品)应等于各段上的概率之积。而该厂总的次品率应等于从“厂”结点到达“次品”结点的所有路径算出的概率之和(全概率公式)。而其中每条路径算出的概率在总概率中所占的比例，就是已知抽取产品结果再推测其来源(路径)的概率(逆概率公式)。根据以上描述，可以算出，该厂的正品率约为(53)。如果上级抽查取出了一个次品，那么该次品属于甲车间生产的概率约为(54)。A．0.963B．0.961C．0.959D．0.957

2.成功率是品在规定的条件下完成规定功能的概率或产品在规定的条件下试验成成功率功的概率。()

3.决策树分类时将该结点的实例强行分到条件概率大的那一类去。()此题为判断题(对，错)。

4.贝叶斯定理实质上是对()的陈述。A、联合概率B、边际概率C、条件概率D、后验概率

更多“怎样从历史数据中训练出结点之间的条件概率或联合条件概率？”相关问题

  • 第1题：

    如果影响利润的因素未来具有不确定性，在已知概率的条件下，可以采用的利润预测方法有()。

    A:趋势分析法

    B:联合概率分析法

    C:经验法

    D:历史数据预测法

    E:期望值分析法


    答案:BE

  • 第2题：

    信封中装有10张奖券，只有1张有奖．从信封中同时抽取2张奖券，中奖的概率记为P；从信封中每次抽取1张奖券后放回，如此重复抽取n次，中奖的概率记为Q．则P

    A.条件（1）充分，但条件（2）不充分；
    B.条件（2）充分，但条件（1）不充分；
    C.条件（1）和条件（2）单独都不充分，但条件（1）和条件（2）联合起来充分；
    D.条件（1）充分，条件（2）也充分；
    E.条件（1）和条件（2）单独都不充分，条件（1）和条件（3）联合起来也不充分．

    答案：B
    解析：

  • 第3题：

    ( )表示两个事件共同发生的概率。

    A.条件概率
    B.联合概率
    C.测度概率
    D.边缘概率

    答案：B
    解析：
    联合概率表示两个事件共同发生的概率。

  • 第4题：

    怎样从历史数据中训练出结点之间的条件概率或联合条件概率？


    正确答案:要训练条件概率P（B|A），可以在历史数据中统计A发生的次数T（A），然后统计在A发生的数据中B发生的次数T（A，B），条件概率P（B|A）=T（B）/T（A）。要训练联合条件概率P（C|A，B），可以在历史数据中统计A、B共同发生的次数T（A，B），然后在A、B共同发生的数据中统计C发生的次数T（A，B，C），联合条件概率P（C|A，B）=T（A，B，C）/T（A，B）。以上的符号A、B、C可以表示某个事件，也可以表示该事件的相反事件。

  • 第5题：

    贝叶斯决策是依据（）的进行决策的方法。

    • A、联合概率
    • B、边际概率
    • C、条件概率
    • D、后验概率

    正确答案:D

  • 第6题：

    事件的初始估计概率是（）

    • A、集合
    • B、后验概率
    • C、条件概率
    • D、先验概率

    正确答案:D

  • 第7题：

    假设条件下的联合概率除以所有假设条件下联合概率之总和，也就是联合概率的相对概率是（）。

    • A、前概率
    • B、条件概率
    • C、联合概率
    • D、后概率
    • E、逆概率

    正确答案:B

  • 第8题：

    按照有关遗传理论或按遗传病的遗传方式，列出有关成员可能有的基因型及产生这种基因型的概率是（）。

    • A、条件概率
    • B、联合概率
    • C、后概率
    • D、前概率
    • E、逆概率

    正确答案:B

  • 第9题：

    多选题
    如果影响利润的因素未来具有不确定性，在已知概率的条件下，可以采用的利润预测方法有（）
    A

    历史数据预测法

    B

    联合概率分析法

    C

    经验法

    D

    趋势分析法

    E

    期望值分析法


    正确答案： C,A
    解析： 暂无解析

  • 第10题：

    单选题
    某一基因型前提下前概率和条件概率所说明的两个事件同时出现的概率是（）。
    A

    逆概率

    B

    条件概率

    C

    联合概率

    D

    前概率

    E

    后概率


    正确答案： D
    解析： 暂无解析

  • 第11题：

    单选题
    遗传咨询中的概率计算不包括（）。
    A

    中概率

    B

    条件概率

    C

    前概率

    D

    联合概率

    E

    后概率


    正确答案： D
    解析： 暂无解析

  • 第12题：

    单选题
    下列关于概率的说法错误的是 ()
    A

    概率的取值范围在0～l之间

    B

    概率常用P表示

    C

    统计上一般将P≤O.5或P≤0.1的事件称为小概率事件

    D

    在一定条件下，肯定发生的事件称为必然事件，其概率等于1


    正确答案： A
    解析： 暂无解析

  • 第13题：

    ● 某轴承厂有甲、 乙、 丙三个车间，各车间生产的轴承数量分别占全厂的40%、 30%、30%，各车间的次品率分别为3%、4%、5%（正品率分别为97%、96%、95%）。以上叙述可以图示如下。

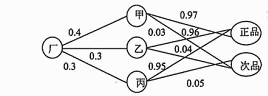
    在图中，从“厂”结点出发选择三个车间产品的概率分别为 0.4、0.3、0.3，从各“车间”结点出发选择“正品”或“次品”的概率如图所示。从“厂”结点出发，到达“正品”（或“次品”）结点，可以有多条路径。例如，路径“厂—甲—次品”表示该厂甲车间生产的次品，其概率 P（厂—甲—次品）应等于各段上的概率之积。而该厂总的次品率应等于从“厂”结点到达“次品”结点的所有路径算出的概率之和（全概率公式）。而其中每条路径算出的概率在总概率中所占的比例，就是已知抽取产品结果再推测其来源（路径）

    的概率（逆概率公式）。根据以上描述，可以算出，该厂的正品率约为 （53） 。如果上级抽查取出了一个次品，那么，该次品属于甲车间生产的概率约为 （54） 。

    （53）

    A. 0.963

    B. 0.961

    C. 0.959

    D. 0.957

    （54）

    A. 0.25

    B. 0.28

    C. 0.31

    D. 0.34


    正确答案：B,C

  • 第14题：

    下列关于概率的几种形式的说法中，正确的有（ ）。
    Ⅰ.条件概率可以用决策树进行计算
    Ⅱ.联合概率表示两个事件共同发生的概率
    Ⅲ.A与B的联合概率表示为P（AB）或者P（A,B）,或者P（A∩B）
    Ⅳ.A的边缘概率表示为P（A|B）

    A.Ⅰ.Ⅲ.Ⅳ
    B.Ⅰ.Ⅱ.Ⅲ.Ⅳ
    C.Ⅰ.Ⅱ.Ⅲ
    D.Ⅱ.Ⅲ.Ⅳ

    答案：C
    解析：
    边缘概率是某个事件发生的概率，而与其他事件无关。边缘概率是这样得到的：在联合概率中，把最终结果中不需要的那些事件合并成其事件的全概率而消失（对离散随机变量用求和得全概率，对连续型随机变量用积分得全概率），这称为边缘化。A的边缘概率表示为P（A），B的边缘概率表示为P（B）。

  • 第15题：

    下列关于概率的几种形式的说法中，正确的有( )。

    Ⅰ．条件概率可以用决策树进行计算

    Ⅱ．联合概率表示两个事件共同发生的概率

    Ⅲ．A与B的联合概率表示为P(AB)或者P(A.B)，或者P(A∩B)Ⅳ．A的边缘概率表示为P(AIB)


    A.Ⅰ、Ⅲ、Ⅳ
    B.Ⅰ、Ⅱ、Ⅲ、Ⅳ
    C.Ⅰ、Ⅱ、Ⅲ
    D.Ⅱ、Ⅲ、Ⅳ

    答案：C
    解析：
    边缘概率，是某个事件发生的概率，而与其他事件无关。边缘概率是这样得到的：在联合概率中，把最终结果中不需要的那些事件合并成其事件的全概率而消失（对离散型随机变量用求和得全概率，对连续型随机变量用积分得全概率），这称为边缘化。A的边缘概率表示为P(A)，B的边缘概率表示为P(B)。

  • 第16题：

    如果叶贝斯网络的各个结点都没有任何证据，从历史数据中如何用两种不同的方法得到各个结点的发生概率？


    正确答案:可以用两种方式从历史数据中得到各个节点的发生概率：
    （1）用各节点的发生次数除以总的数据条数，就是各个节点的发生概率。
    （2）首先，用第一种方法计算原因节点的发生概率，然后计算原因节点到中间节点或结果节点的条件概率，最后根据原因节点的概率和这些条件概率计算结果节点的概率。

  • 第17题：

    遗传咨询中的概率计算不包括（）。

    • A、中概率
    • B、条件概率
    • C、前概率
    • D、联合概率
    • E、后概率

    正确答案:E

  • 第18题：

    事件A的发生概率是在事件B发生概率的前提下的条件概率，记作（）。


    正确答案:P(A|B)

  • 第19题：

    某一基因型前提下前概率和条件概率所说明的两个事件同时出现的概率是（）。

    • A、逆概率
    • B、条件概率
    • C、联合概率
    • D、前概率
    • E、后概率

    正确答案:D

  • 第20题：

    概率分布必须符合以下两个条件：所有的概率Pi均在0和1之间；所以结果的概率之和应等于1。


    正确答案:正确

  • 第21题：

    单选题
    贝叶斯决策是依据（）的进行决策的方法。
    A

    联合概率

    B

    边际概率

    C

    条件概率

    D

    后验概率


    正确答案： C
    解析： 暂无解析

  • 第22题：

    单选题
    假设条件下的联合概率除以所有假设条件下联合概率之总和，也就是联合概率的相对概率是（）。
    A

    前概率

    B

    条件概率

    C

    联合概率

    D

    后概率

    E

    逆概率


    正确答案： A
    解析： 暂无解析

  • 第23题：

    单选题
    贝叶斯定理实质上是对（）的陈述。
    A

    联合概率

    B

    边际概率

    C

    条件概率

    D

    后验概率


    正确答案： C
    解析： 暂无解析

  • 第24题：

    单选题
    按照有关遗传理论或按遗传病的遗传方式，列出有关成员可能有的基因型及产生这种基因型的概率是（）。
    A

    条件概率

    B

    联合概率

    C

    后概率

    D

    前概率

    E

    逆概率


    正确答案： D
    解析： 暂无解析

相关内容