3、通用近似定理说明A.多层感知机可以做为函数近似器逼近任意函数B.只需一个隐藏层的多层感知机就能作为通用函数近似器,因此没必要设计深层网络C.给定隐藏层神经元,三层感知机可以近似任意从一个有限维空间到另一个有限维空间的Borel 可测函数D.以上全不对
题目
3、通用近似定理说明
A.多层感知机可以做为函数近似器逼近任意函数
B.只需一个隐藏层的多层感知机就能作为通用函数近似器,因此没必要设计深层网络
C.给定隐藏层神经元,三层感知机可以近似任意从一个有限维空间到另一个有限维空间的Borel 可测函数
D.以上全不对
相似考题
更多“3、通用近似定理说明”相关问题
-
第1题:
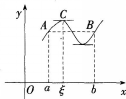
罗尔定理:设函数(x)满足条件:(1)在闭区间[a,b]上连续;(2)在开区间(a,b)内可导;(3)(a)=(b),则在(a,b)内至少存在一点ξ,使得,′(ξ)=0。证明这个定理并说明其几何意义。答案:解析:
-
第2题:
根据中心极限定理,抽样分布近似于正态分布时样本的规模的判断起点是()
A30
B50
C70
D100
D
略 -
第3题:
职业技能鉴定理论知识部分采用()的执行标准进行评判。
- A、常用
- B、适用
- C、通用
- D、实用
正确答案:C -
第4题:
中心极限定理告诉我们,不管总体服从什么分布,其()的分布总是近似服从正态分布。
正确答案:大容量样本均值 -
第5题:
需求定理说明,一种物品价格上升使该物品需求减少。
正确答案:错误 -
第6题:
一个总体有150个个体,从该总体中抽取24个观察值作为样本。x-的抽样分布()。
- A、近似正态分布,因为x-总是近似正态分布
- B、近似正态分布,因为相对于总体,样本容量足够大
- C、近似正态分布,因为中心极限定理
- D、如果总体服从正态分布,那它也是正态分布
正确答案:D -
第7题:
说明伯努利方程中各项参数的物理意义。并利用伯努利定理说明气流速度变化与气流压强变化的关系。
正确答案: 动压,单位体积空气所具有的动能。这是一种附加的压力,是空气在流动中受阻,流速降低时产生的压力。静压,单位体积空气所具有的压力能。在静止的空气中,静压等于当时当地的大气压。总压(全压),它是动压和静压之和。总压可以理解为,气流速度减小到零之点的静压。气流速度增加,动压增加,为了保持总压不变,气流压强即静压必需减小。 -
第8题:
商标法禁止商标使用的文字和图形有()
- A、同“红新月”的标志近似的图形
- B、同外国的国旗相同或近似的图形
- C、县级以上行政区划的地名
- D、本商品的通用名称
正确答案:A,B,C,D -
第9题:
问答题试说明欧拉定理在要素收入分配理论中的含义。正确答案: 欧拉定理是一个数学结论,在经济学中的说法是:如果生产服从规模收益不变,那么每种生产要素按边际产量取得收入恰好等于它们的总产量。用公式表示为:y=MPLL+MPKK
这一结论对于边际分配论具有很强的解释意义。在完全竞争市场上,当所有的要素市场处于均衡状态的时,厂商要素的均衡使用量所对应的边际产品价值恰好等于此时的要素价格。根据欧拉定理的结论,在厂商的生产处于规模收益不变时,要素按照这一价格取得的收入恰好等于所有的产量(的价值)。因此,定理的结论表明,按照要素的边际产品进行分配是合理的制度。解析: 暂无解析 -
第10题:
单选题职业技能鉴定理论知识部分采用()的执行标准进行评判。A常用
B适用
C通用
D实用
正确答案: B解析: 暂无解析 -
第11题:
单选题根据(),无论总体服从什么分布,只要样本量足够大,来自这个总体的随机样本的均值呈近似正态分布。A大数定理
B中心极限定理
C最小二乘法
D正态分布特性
正确答案: D解析: 暂无解析 -
第12题:
单选题根据中心极限定理,抽样分布近似于正态分布时样本的规模的判断起点是()A30
B50
C70
D100
正确答案: C解析: 暂无解析 -
第13题:
针对“角平分线的性质定理”的内容,请你完成下列任务:
(1)叙述角平分线的性质定理; (5分)
(2)设计“角平分线的性质定理“教学过程(只要求写出新课导入、定理形成与证明过程),并说明设计意图; (20分)
(3)借助“角平分线的性质定理”,简述如何帮助学生积累认识几何图形的数学活动经验.(5分)答案:解析:(1)角平分线上的点到角两边的距离相等。 (2)新课导入:
教师:我们应该在很早之前就接触过角的平分线这个概念,谁能告诉我什么是角的平分线呢
(学生回答)一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线。
教师:大家观察一下这个角,其实,再添加一些线段就能成为两个三角形,我们之前学习了全等三角形的性质及判定,那么结合这个,我们是否能够发现角的平分线的一些性质呢今天我们就来探究一 下这个问题。
设计意图:复习角平分线的定义,并为角平分线的性质定理的引出做铺垫,为下一步设置问题通过折纸及作图过程,由学生自己去发现结论。
教学活动:任意作-一个角∠AOB, 作出∠AOB的平分线OC,在OC上任取一点P,过点P画出OA和OB的垂线, 分别记垂足为D, E,PD和PE有什么关系引导学生猜想。
教师:大家可以用直尺来量测一下,能够得到结论吗
大部分同学都得到了PD=PE的结论。 那么有谁能够利用数学方法来证明一下呢
已知:如图,∠AOC=∠BOC, 点P在0C上,PD⊥OA,PE⊥OB,垂足分别为D,E。
求证: PD=PE。
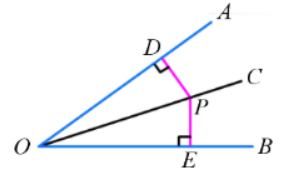
师生共同证明:
∵PD⊥OA,PE⊥OB
∴∠PDO=∠PEO=90°
在ΔPDO和ΔPEO中
∠PDO=∠PEO (已证)
∠AOC=∠BOC
OP=OP (公共边)
∴ΔPDO≌ΔPEO (AAS)
∴PD=PE (全等三角形的对应边相等)
得到角平分线性质:角的平分线上的点到角的两边的距离相等。
教师:通过刚刚的证明,我们得到了我们的结论是正确的。是不是在角平分线上任意取点,都可以得到这个结论呢
(学生动手验证)
教师:我们发现,任意一点都可以得到相等的结论。由此,我们得到了角平分线的性质:
角平分线上的点到角的两边的距离相等。
结论数学语言:
∵OP平分∠AOB,PD⊥OA,PE⊥OB
∴PD=PE。
教师:在这个定理中,我们必须明白,这个性质的应用必须满足几个条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离。
设计意图:让学生通过实验发现、分析概括、推理证明角的平分线的性质,体会研究几何问题的基本思路,以角的平分线的性质的证明为例,让学生概括几何名命题的-般步骤,发展学生的归纳概括能力。
(3)数学活动经验是一种 属于学生自己的“主观性认识”,对于认识几何图形的数学活动经验,是学生经过数学学习后对整个数学活动过程产生的认识。如何帮助学生积累认识几何图形的数学活动经验,首先要联系直观图形,把生活经验转化为基本数学活动经验。学生在生活中已经积累的一些关于数学的原始、初步的经验,因此要善于捕捉生活中的数学现象,挖掘数学知识的生活内涵,让学生亲身经历将生活经验转化为数学活动经验的过程。例如在本节课中,可以先让学生画一个角,然后探究角平分线的作法。利用模型教具说明平分角的仪器的工作原理,从中受到启发,利用尺规做角的平分线,进-步思考角的平分线上的点的特征。
其次要引导观察、思考推理,丰富学生思维的经验。 积累活动经验总得依赖一些活动,但是所谓的活动并不-定是指直观的操作活动,行为操作的经验是基本活动经验,抽象的思考、探究的经验也是基本活动经验的重要组成部分。例如在本节课中,教师在抛出“PD和PE有什么关系之后,教师先引导学生进行猜想,再带领学生进行自主探究去证明,对于不同的学生想出证明方法可能都不一样,所以教师可以组织学生进行汇报交流,最后师生共同总结得到证明方法:最終得到角平分线定理的性质。 -
第14题:
气体流量所用到Nm3/h单位中,下列说法正确的是()
- A、Nm3—表示近似等于立方米
- B、Nm3—就等于立方米
- C、Nm3—表示标准立方米
- D、Nm3—表示国际通用的立方米
正确答案:C -
第15题:
试说明欧拉定理在要素收入分配理论中的含义。
正确答案: 欧拉定理是一个数学结论,在经济学中的说法是:如果生产服从规模收益不变,那么每种生产要素按边际产量取得收入恰好等于它们的总产量。用公式表示为:y=MPLL+MPKK
这一结论对于边际分配论具有很强的解释意义。在完全竞争市场上,当所有的要素市场处于均衡状态的时,厂商要素的均衡使用量所对应的边际产品价值恰好等于此时的要素价格。根据欧拉定理的结论,在厂商的生产处于规模收益不变时,要素按照这一价格取得的收入恰好等于所有的产量(的价值)。因此,定理的结论表明,按照要素的边际产品进行分配是合理的制度。 -
第16题:
根据中心极限定理,抽样分布近似于正态分布时样本的规模的判断起点是()
- A、30
- B、50
- C、70
- D、100
正确答案:D -
第17题:
从一个无限总体中抽取92个观察值作为样本。x-的抽样分布近似于()。
- A、正态分布,因为总是近似正态分布
- B、正态分布,因为相对于总体,样本容量足够大
- C、正态分布,因为中心极限定理
- D、以上均错误
正确答案:D -
第18题:
当样本容量足够大时,允许我们使用正态概率分布来近似样本均值和样本成数的抽样分布,这种定理是()。
- A、近似定理
- B、正态概率定理
- C、中心极限定理
- D、中心正态定理
正确答案:C -
第19题:
举例说明什么叫概率的乘法定理和概率的加法定理?
正确答案:概率的乘法定理:是指两个独立事件同时发生或相继发生的概率等于他们各个概率的乘积。概率的加法定理:是指两个或几个互斥事件构成的复合事件发生的概率等于各事件概率之和。例如:两个杂合体(Rr)自交,后代的基因组和可能是RR、Rr、rR、rr,各事件概率均为1/4,那么后代中基因行为Rr的概率是1/4+1/4=1/2。 -
第20题:
阿罗的不可能性定理说明了什么问题?
正确答案:要点如下:
第一、根据阿罗的不可能性定理,在非独裁的情况下,不可能存在有适用于所有个人偏好类型的社会福利函数。
第二、阿罗的不可能性定理意味着,不能从不同个人的偏好当中合理地形成所谓的社会偏好。换句话说,一般意义上的社会福利函数并不存在.这表明,西方经济学没有能彻底地解决资源配置问题。 -
第21题:
问答题举例说明什么叫概率的乘法定理和概率的加法定理?正确答案: 概率的乘法定理:是指两个独立事件同时发生或相继发生的概率等于他们各个概率的乘积。概率的加法定理:是指两个或几个互斥事件构成的复合事件发生的概率等于各事件概率之和。例如:两个杂合体(Rr)自交,后代的基因组和可能是RR、Rr、rR、rr,各事件概率均为1/4,那么后代中基因行为Rr的概率是1/4+1/4=1/2。解析: 暂无解析 -
第22题:
填空题相似第一定理说明了,()或者()是相似的必要条件。正确答案: 相似指标为1,相似判据相等解析: 暂无解析 -
第23题:
问答题试说明伯努利定理及其物理意义?正确答案: 伯努利定理是能量守恒定律在流体流动中的应用。伯努利定理是描述流体在流动过程中流体压强和流速之间关系的流动规律。在管道中稳定流动的不可压缩理想流体,在管道各处的流体动压和静压之和应始终保持不变即:静压+动压=总压=常数,上式就是不可压缩流体的伯努利方程,它表示流速与静压之间的关系,即流体流速增加,流体静压将减小;反之,流动速度减小,流体静压将增加。解析: 暂无解析 -
第24题:
填空题中心极限定理告诉我们,不管总体服从什么分布,其()的分布总是近似服从正态分布。正确答案: 大容量样本均值解析: 暂无解析
