2、已知点M（-4,-5)，线段MN的中点坐标为（1，-2），则线段端点N的坐标为（）A．（6,1）B．（-6，-1）C．（1，-6）D．（-6,1）E．（1,6）

题目

2、已知点M（-4,-5)，线段MN的中点坐标为（1，-2），则线段端点N的坐标为（）

A．（6,1）

B．（-6，-1）

C．（1，-6）

D．（-6,1）

E．（1,6）

相似考题

1.已知过点（0，4），斜率为-1的直线l与抛物线C：y2—2px（b&gt；0）交于A，B两点．（I）求C的顶点到2的距离；（Ⅱ）若线段AB中点的横坐标为6，求C的焦点坐标．

2.线段A(-6，1)、B(8，-3)的中点坐标为( )。A.(-7,-1)B.(-7,-2)C.(1,-2)D.(1,-1)

3.已知A、B两点的坐标为 XA=1011.358m, YA=1185.395m;点B的坐标为XB=883.122m,YB=1284.855m。在AB线段的延长线上定出一点C，BC间的距离DBC=50.000m，计算C点的坐标。

4.图块定义中插入点的系统默认值为?()A.坐标原点B.线段端点C.用户指定D.通常不为同一点

更多“2、已知点M（-4,-5)，线段MN的中点坐标为（1，-2），则线段端点N的坐标为（）”相关问题

  • 第1题：

    在平面直角坐标系中，将坐标为（0，0），（2，4），（2，0），（4，4）的点用线段依次连接起来形成一个图案。

    （1）这四个点的纵坐标保持不变 ，横坐标变为原来的½，将所得的四个点用线段依次连接起来，所得的图案与原图案相比有什么变化。

    （2）纵坐标保持不变，横坐标分别加3呢？

    （3）横坐标保持不变，纵坐标分别加3呢？

    （4）纵坐标保持不变，横坐标分别乘-1呢？

    （5）纵、横坐标分别变为原来的2倍呢？

    （6）横坐标保持不变，纵坐标分别乘以-1呢？

  • 第2题：

    建立平面直角坐标系，并描出下列各点：

    A（1， 1）， B（5， 1）， C（3， 3）， D（-3， 3）， E（1， -2）， F（1， 4），G（3， 2）， H（3， -2），I（-1， -1）， J（-1， 1）。

    连接AB，CD，EF，GH，IJ，找出它们中点的坐标，将上述中点的横坐标和纵坐标分别与对应线段的两个端点的横坐标和纵坐标进行比较，你发现它们之间有什么关系？写出你的发现，并与其他同学进行交流。

  • 第3题：

    设L为从点A（0，-2）到点B（2，0）的有向直线段，则对坐标的曲线积分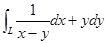

    等于（　　）。

    A、 1
    B、 -1
    C、 3
    D、 -3

    答案：D
    解析：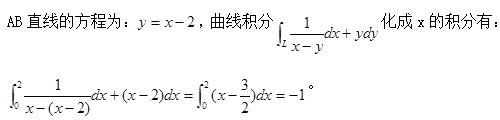

  • 第4题：

    已知点则点P的坐标为( )

    A.(2，7/2)
    B.(0，4)
    C.(8，2)
    D.(2，1)

    答案：B
    解析：
    【考情点拨】本题主要考查的知识点为向量的坐标运算． 【应试指导】由题意得：

  • 第5题：

    已知线段AB的长为12,点A的坐标是（一4,8）,点B横、纵坐标相等,则点B的坐标为（ ）

    A.（-4,-4）
    B.（8,8）
    C.（4,4）或（8,8）
    D.（-4,-4）或（8,8）
    E.（4,4）或（-8,-8）

    答案：D
    解析：

  • 第6题：

    C是线段AB上一点，D是线段CB的中点，已知图中所有线段的长度之和为23，线段 AC和线段CB的长度都是正整数,那么线段4C的长度为：



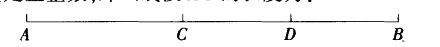    A.2
    B.3
    C.5
    D.7

    答案：B
    解析：
    。解析是Cfl的中点’CD=DB=1/2CB。所有线段长度之和=4C+AD+AB+CD+CB+DB=AC+(AC+

  • 第7题：

    已知两点M(5,3,2)、N(1,-4,6),则单位向量MN0可表示为（ ）。


    答案：B
    解析：

  • 第8题：

    由一条线段的一个端点坐标、线段长及方位角计算另一端点坐标的计算方法称为()。

    A:高斯反算
    B:坐标反算
    C:高斯正算
    D:坐标正算

    答案：D
    解析：
    由一条线段的一个端点坐标、线段长及方位角计算另一端点坐标的计算称为坐标正算，由两端点坐标计算线段长和方位角称为坐标反算；由大地坐标计算高斯平面坐标（椭球面到平面）称为高斯正算；由高斯平面坐标计算大地坐标称为高斯反算。故选D。

  • 第9题：

    设抛物线y2=2px(p>0)焦点为F，点A坐标为(0，2)，若线段FA的中点B在抛物线上，则B到该抛物线准线距离为__________。


    答案：
    解析：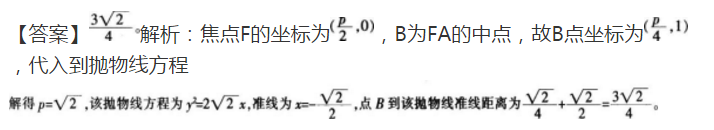

  • 第10题：

    如果线段端点坐标值不是整数，采用DDA算法产生的直线和将端点坐标值先取整后再用Bressenham算法产生的直线是否完全相同？为什么？能否扩充整数Bressenham算法使之能够处理当线段端点坐标值不是整数的情况。


    正确答案:不相同。因为DDA算法总是选择△x或者△y中的较大者作为步进的方向，不失一般性，假设选择x方向，则x方向每前进一个像素点，y方向前进的像素点个数应该在[0，1]区间，但是由于采用了（向上或者向下或者四舍五入）取整运算，必然会导致某些像素点偏在了真实直线的一侧。而Bressenham算法每一步都会根据实际直线与网格的距离来决定下一个像素点的选择，因此所选像素点更加贴近于真实的直线。可以扩充整数Bressenham算法使之能够处理当线段端点坐标值不是整数的情况。

  • 第11题：

    已知线段AB的水平距离为200米，线段AB的方位角为133°10′22″，则线段AB的X轴方向的坐标增量为（）

    • A、+145.859
    • B、-145.859
    • C、+136.840
    • D、-136.840

    正确答案:D

  • 第12题：

    问答题
    如果线段端点坐标值不是整数，采用DDA算法产生的直线和将端点坐标值先取整后再用Bressenham算法产生的直线是否完全相同？为什么？能否扩充整数Bressenham算法使之能够处理当线段端点坐标值不是整数的情况。

    正确答案： 不相同。因为DDA算法总是选择△x或者△y中的较大者作为步进的方向，不失一般性，假设选择x方向，则x方向每前进一个像素点，y方向前进的像素点个数应该在[0，1]区间，但是由于采用了（向上或者向下或者四舍五入）取整运算，必然会导致某些像素点偏在了真实直线的一侧。而Bressenham算法每一步都会根据实际直线与网格的距离来决定下一个像素点的选择，因此所选像素点更加贴近于真实的直线。可以扩充整数Bressenham算法使之能够处理当线段端点坐标值不是整数的情况。
    解析： 暂无解析

  • 第13题：

    在直角坐标系中，将坐标是（2，0），（2，2），（0，2），（0，3），（2，5），（3，5），（2，2），（5，3），（5，2），（3，0），（2，0）的点用线段依次连接起来形成一个图案。

    （1）每个点的横坐标保持不变，纵坐标变成原来的½，再将所得的各个点用线段依次连接起来，所得的图案与原图案相比有什么变化。

    （2）纵坐标保持不变，横坐标分别加3呢？

    （3）横坐标保持不变，纵坐标分别加3呢？

    （4）纵坐标保持不变，横坐标分别乘-1呢？

    （5）纵、横坐标分别变为原来的2倍呢？

    （6）横坐标保持不变，纵坐标分别乘以-1呢？

  • 第14题：

    已知点A的坐标为(2,－1),AB=4,AB∥X轴,则B点的坐标为_________


    正确答案：
     (－2，－1)，（6，－1） 

  • 第15题：

    已知线段AB被点C(2，0，2)和D(5，-2，0)三等分，则端点A和B的坐标为（　　）．

    A.A(-1，2，4)，B(8，-4，-2)
    B.A(1，2，4)，B(8，4，-2)
    C.A(-1，2，4)，B(-8，-4，-2)
    D.A(-1，2，4)，B(-8，4，-2)

    答案：A
    解析：

  • 第16题：

    若A（-3,5），B（-5,-3），则线段AB中点的坐标为（　　）

    A.（4,-1）
    B.（-4,1）
    C.（-2,4）
    D.（-1,2）

    答案：B
    解析：

  • 第17题：

    已知点C（2,-3）,M（1,2）,N（-1,-5）,则点C到直线MN的距离等于（ ）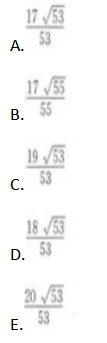


    答案：A
    解析：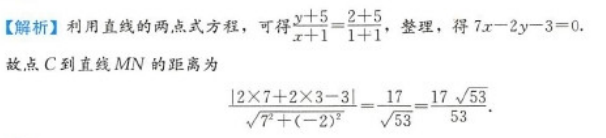

  • 第18题：

    在直角三角形ABC中，点D是斜边AB的中点，点P为线段CD的中点，则( )。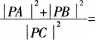

    A、2
    B、4
    C、5
    D、10

    答案：D
    解析：
    本题主要考查两点问的距离公式，以及坐标法这一重要的解题方法和数形结合的数学思

  • 第19题：

    设L为从点A（0，-2）到点B（2，0）的有向直线段，则对坐标的曲线积分



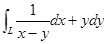
    等于（　　）。

    A.1
    B.-1
    C.3
    D.-3

    答案：B
    解析：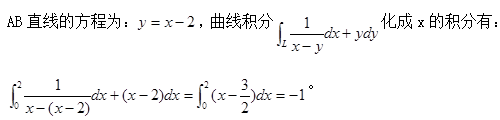


    @##

  • 第20题：

    如图，Rt△ABC中，AB=6，BC=4，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为__________。



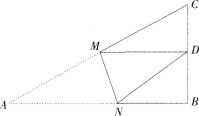    答案：
    解析：

  • 第21题：

    线段A（-6，1）、B（8，-3）的中点坐标为（）。

    • A、（1，－1）
    • B、（-7，-2）
    • C、（1，-2）
    • D、（-7，-1）

    正确答案:A

  • 第22题：

    图块定义中插入点的系统默认值为：（）

    • A、线段端点
    • B、坐标原点
    • C、用户指定
    • D、通常不为同一点

    正确答案:B

  • 第23题：

    坐标正算，是根据某直线段两个端点的已知坐标，计算该直线段的水平距离和坐标方位角的工作。


    正确答案:错误

  • 第24题：

    单选题
    线段AB平行于y轴，且|AB|＝6，若点A的坐标为（3，2），则点B的坐标是（　　）．
    A

    （9，2）或（－3，2）

    B

    （3，8）

    C

    （3，4）

    D

    （3，8）或（3，－4）


    正确答案： A
    解析：
    ∵AB∥y轴，∴B点坐标可写为（3，y），又∵|AB|＝6, ∴|y－2|＝6，y＝8或y＝－4．故B点坐标是（3，8）或（3，－4）．

相关内容