p(x)是数域P上的不可约多项式,则p(x)不整除f(x)且p(x)不整除g(x),则p(x)不整除f(x)g(x)。
题目
p(x)是数域P上的不可约多项式,则p(x)不整除f(x)且p(x)不整除g(x),则p(x)不整除f(x)g(x)。
相似考题
更多“p(x)是数域P上的不可约多项式,则p(x)不整除f(x)且p(x)不整除g(x),则p(x)不整除f(x)g(x)。”相关问题
-
第1题:
设 f(x)ϵP[x] ,
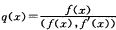 ,则f(x)与q(x)的关系是()
,则f(x)与q(x)的关系是()A.
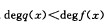
B.

C.
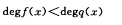
D.
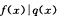 参考答案:B
参考答案:B
-
第2题:
两个本原多项式g(x)和f(x),令h(x)=g(x)f(x)记作Cs,若h(x)不是本原多项式,则存在p当满足什么条件时使得p|Cs(s=0,1…)成立?()
- A、p是奇数
- B、p是偶数
- C、p是合数
- D、p是素数
正确答案:D -
第3题:
在F[x]中从p(x)|f(x)g(x)可以推出什么?()
- A、p(x)
- B、p(x)
- C、p(x)
- D、g(x)f(x)
正确答案:A -
第4题:
若p(x)是F(x)中次数大于0的不可约多项式,那么可以得到下列哪些结论?()
- A、只能有(p(x),f(x))=1
- B、只能有(p(x)
- C、(p(x),f(x))=1或者(p(x)
- D、(p(x),f(x))=1或者(p(x)
正确答案:D -
第5题:
在F[x]中,若g(x)|fi(x),其中i=1,2…s,则对于任意u1(x)…us(x)∈F(x),u1(x)f1(x)+…us(x)fs(x)可以被谁整除?()
- A、g(ux)
- B、g(u(x))
- C、u(g(x))
- D、g(x)
正确答案:D -
第6题:
在数域K中多项式f(x)与g(x)若有f=g,则f(x)=g(x)。
正确答案:正确 -
第7题:
单选题若p/q是f(x)的根,其中(p,q)=1,则f(x)=(px-q)g(x),当x=1时,f(1)/(p-q)是什么?()A复数
B无理数
C小数
D整数
正确答案: B解析: 暂无解析 -
第8题:
单选题若有语句:int x,*p=&x;则与该语句等价的语句是()Aintx,*p;*p=&x;
Bint x,*p;p=&x;
Cint x,*p;*p=x;
Dint x,*p;p=x
正确答案: B解析: 暂无解析 -
第9题:
问答题判断下列公式是否为可合一,若可合一,则求出其最一般合一。 (1)P(a,b),P(x,y) (2)P(f(x),b),P(y,z) (3)P(f(x),y),P(y,f(b)) (4)P(f(y),y,x),P(x,f(a),f(b)) (5)P(x,y),P(y,x)正确答案: (1)可合一,其最一般和一为:σ={a/x,b/y}。
(2)可合一,其最一般和一为:σ={y/f(x),b/z}。
(3)可合一,其最一般和一为:σ={fB./y,b/x}。
(4)不可合一。
(5)可合一,其最一般和一为:σ={y/x}。解析: 暂无解析 -
第10题:
单选题两个本原多项式g(x)和f(x),令h(x)=g(x)f(x)记作Cs,若h(x)不是本原多项式,则存在p当满足什么条件时使得p|Cs(s=0,1…)成立?()Ap是奇数
Bp是偶数
Cp是合数
Dp是素数
正确答案: D解析: 暂无解析 -
第11题:
填空题若X~P(λ)且P{X=2}=P{X=3},则E(X)=____。D(X)=____。正确答案: 3,3解析:
根据题意P{X=2}=P{X=3},即λ2e-λ/2!=λ3e-λ/3!,解得λ=3,故E(X)=D(X)=λ=3。 -
第12题:
单选题对于任意f(x)∈F[x],f(x)都可以整除哪个多项式?()Af(x+c)c为任意常数
B0.0
C任意g(x)∈F{x]
D不存在这个多项式
正确答案: A解析: 暂无解析 -
第13题:
判断下列公式是否为可合一,若可合一,则求出其最一般合一。 (1)P(a,b),P(x,y) (2)P(f(x),b),P(y,z) (3)P(f(x),y),P(y,f(b)) (4)P(f(y),y,x),P(x,f(a),f(b)) (5)P(x,y),P(y,x)
正确答案: (1)可合一,其最一般和一为:σ={a/x,b/y}。
(2)可合一,其最一般和一为:σ={y/f(x),b/z}。
(3)可合一,其最一般和一为:σ={fB./y,b/x}。
(4)不可合一。
(5)可合一,其最一般和一为:σ={y/x}。 -
第14题:
通过四个互异节点的插值多项式p(x),只要满足(),则p(x)是不超过二次的多项式。
正确答案:满足三阶均差为0 -
第15题:
对于任意f(x)∈F[x],f(x)都可以整除哪个多项式?()
- A、f(x+c)c为任意常数
- B、0.0
- C、任意g(x)∈F{x]
- D、不存在这个多项式
正确答案:B -
第16题:
下列结论正确的是()
- A、P(x1≤ξ≤x2)=F(x2)-F(x1)
- B、(-x)=1-Φ(x)
- C、P(AB)=P(A)P(B)
- D、P(A+B)=P(A)+P(B)
正确答案:A,B -
第17题:
若p/q是f(x)的根,其中(p,q)=1,则f(x)=(px-q)g(x),当x=1时,f(1)/(p-q)是什么?()
- A、复数
- B、无理数
- C、小数
- D、整数
正确答案:D -
第18题:
单选题若p(x)是F(x)中次数大于0的不可约多项式,那么可以得到下列哪些结论?()A只能有(p(x),f(x))=1
B只能有(p(x)
C(p(x),f(x))=1或者(p(x)
D(p(x),f(x))=1或者(p(x)
正确答案: D解析: 暂无解析 -
第19题:
填空题通过四个互异节点的插值多项式p(x),只要满足(),则p(x)是不超过二次的多项式。正确答案: 满足三阶均差为0解析: 暂无解析 -
第20题:
单选题在F[x]中,若g(x)|fi(x),其中i=1,2…s,则对于任意u1(x)…us(x)∈F(x),u1(x)f1(x)+…us(x)fs(x)可以被谁整除?()Ag(ux)
Bg(u(x))
Cu(g(x))
Dg(x)
正确答案: A解析: 暂无解析 -
第21题:
单选题在F[x]中从p(x)|f(x)g(x)可以推出什么?()Ap(x)
Bp(x)
Cp(x)
Dg(x)f(x)
正确答案: D解析: 暂无解析 -
第22题:
单选题设y1(x)是方程y′+P(x)y=f1(x)的一个解,y2(x)是方程y′+P(x)y=f2(x)的一个解,则y=y1(x)+y2(x)是方程( )的解。Ay′+P(x)y=f1(x)+f2(x)
By+P(x)y′=f1(x)-f2(x)
Cy+P(x)y′=f1(x)+f2(x)
Dy′+P(x)y=f1(x)-f2(x)
正确答案: A解析:
根据题意可知,y1′+P(x)y1=f1(x),y2′+P(x)y2=f2(x)。两式相加得(y1′+y2′)+P(x)(y1+y2)=f1(x)+f2(x)。则可发现y=y1+y2是方程y′+P(x)y=f1(x)+f2(x)的解。 -
第23题:
判断题在数域K中多项式f(x)与g(x)若有f=g,则f(x)=g(x)。A对
B错
正确答案: 对解析: 暂无解析 -
第24题:
单选题设X~N(2,22),其概率密度函数为f(x),分布函数F(x),则( )。AP{X≤0}=P{X≥0}=0.5
Bf(-x)=1-f(x)
CF(x)=-F(-x)
DP{X≥2}=P{X<2}=0.5
正确答案: B解析:
该正态分布的密度函数的图像关于x=μ=2对称,故P{X≥2}=P{X<2}=0.5,故应选D。
