对分区间法就是运用零点存在定理，将区间反复减半，直到区间长度满足精度要求。

题目

对分区间法就是运用零点存在定理，将区间反复减半，直到区间长度满足精度要求。

相似考题

1.利用回归模型对我国 GDP 进行区间预测时，下列说法中正确的是（ ）。A．为了提高预测精度，预测区间越大越好B．为了提高预测精度，预测区间越小越好C．为了提高预测的把握程度（置信水平），预测区间越大越好D．为了提高预测的把握程度（置信水平），预测区间越小越好

2.某一特定的X水平上，总体Y分布的离散度越大，即σ2越大，则（）。A.预测区间越宽，精度越低B.预测区间越宽，预测误差越小C.预测区间越窄，精度越高D.预测区间越窄，预测误差越大

3.在(－1,1)区间上满足罗定理条件的函数是()A、y=xB、y=1/xC、y=x²D、y=/x/

4.下列关于点估计和区间估计的说法正确的是( )。A．点估计仅仅给出了参数的一个具体估计值，而区间估计用区间来估计，区间估计体现了估计的精度B．区间估计用区间范围来估计，而点估计给出了参数的一个具体估计值，点估计体现了估计的精度C．点估计通过具体的数估计了一定区间，而区间估计通过一个范围估计了区间，因此不如点估计精确D．点估计和区间估计是两种不同的估计方法，其精度是一样的

更多“对分区间法就是运用零点存在定理，将区间反复减半，直到区间长度满足精度要求。”相关问题

  • 第1题：

    以下关于置信区间与精度的关系说法不正确的是

    A、当置信度1-α增大，又样本容量n固定时，置信区间长度增加，区间估计精度减低

    B、置信区间的长度可视为区间估计的精度

    C、当置信度1-α减小，又样本容量n固定，置信区间长度减小，区间估计精度提高

    D、置信度1-α固定，当样本容量n增大时，置信区间长度增加，区间估计精度减低


    正确答案:D

  • 第2题：

    在有关区间估计的表述中,正确的是()

    A、标准误越小，区间估计的精度越好

    B、标准误越小，区间估计的精度越差

    C、可信度越大，估计的区间精度越好

    D、可信度越大，估计的区间精度越差

    E、区间估计的精度由标准误与可信度决定


    参考答案：ADE

  • 第3题：


    A.预测区间越宽，精度越低
    B.预测区间越宽，预测误差越小
    C.预测区间越窄，精度越高
    D.预测区间越窄，预测误差越大

    答案：A
    解析：

  • 第4题：

    罗尔定理：设函数(x)满足条件：(1)在闭区间[a，b]上连续；(2)在开区间(a，b)内可导；(3)(a)=(b)，则在(a，b)内至少存在一点ξ，使得，′(ξ)=0。证明这个定理并说明其几何意义。


    答案：
    解析：

  • 第5题：

    某一特定的X水平上，总体Y分布的离散度越大，即σ2越大，则（）。

    • A、预测区间越宽，精度越低
    • B、预测区间越宽，预测误差越小
    • C、预测区间越窄，精度越高
    • D、预测区间越窄，预测误差越大

    正确答案:A

  • 第6题：

    关于关联的可信区间的说法，下列哪些是正确的（）

    • A、可信区间较宽表明RR的精度较差、区间较窄、提示精度较高
    • B、可信区间较宽表明RR的精度较高、区间较窄、提示精度较差
    • C、研究对象数量越大、可信区间越宽、精确度越差
    • D、研究对象数量越大、可信区间越窄、精确度越高
    • E、以上都不对

    正确答案:A,D

  • 第7题：

    ZPW-2000A型轨道电路对分路死区间是如何要求的？


    正确答案:在最不利条件下，用0.15Ω标准分路线分路，主轨道无分路死区段。调谐区分路死区不大于5m（信号机内方开始计算）。

  • 第8题：

    关于置信区间，下列叙述哪项不正确（）。

    • A、置信区间的准确度反映在置信度1－α的大小
    • B、置信区间的精度反映在区间的长度
    • C、在样本例数确定的情况下，上述二者是矛盾的
    • D、99%置信区间比95%置信区间好
    • E、在置信度确定的情况下，增加样本例数可提高精度

    正确答案:D

  • 第9题：

    单选题
    下列说法正确的是(　　)。
    A

    区间估计用区间范围来估计，而点估计给出了参数的一个具体估计值，点估计体现了估计的精度

    B

    点估计仅仅给出了参数的一个具体估计值，而区间估计用区间来估计，区间估计体现了估计的精度

    C

    点估计通过具体的数估计了一定区间，而区间估计通过一个范围估计了区间，因此不如点估计精确

    D

    点估计和区间估计是两种不同的估计方法，其精度是一样的


    正确答案： A
    解析： 暂无解析

  • 第10题：

    问答题
    ZPW-2000A型轨道电路对分路死区间是如何要求的？

    正确答案： 在最不利条件下，用0.15Ω标准分路线分路，主轨道无分路死区段。调谐区分路死区不大于5m（信号机内方开始计算）。
    解析： 暂无解析

  • 第11题：

    单选题
    下列关于区间估计的说法，正确的是（）
    A

    在进行区间估计时，置信区间的长度和估计的精度成正比

    B

    在进行区间估计时，置信区间的长度和估计的精度成反比

    C

    在进行区间估计时，置信概率和估计的可靠程度成反比

    D

    在进行区间估计时，估计的可靠程度和精确程度是无关的


    正确答案： B
    解析： 考查：区间估计的有关概念。区间估计既给出了抽样估计的可靠程度，又给出其精度。其中置信概率是可靠程度的度量，而置信区间的长度则表达了估计的精确程度。置信概率越大，估计的可靠程度越高；置信区间的长度越短，估计的精度则越高。很显然，区间估计的可靠程度和精确程度是相互矛盾的，要提高可靠程度就要增大置信概率，从而就要增加置信区间的长度使估计的精度降低；反之要提高估计的精度就要缩短置信区间的长度，从而就要减小置信概率使估计的可靠程度降低。

  • 第12题：

    单选题
    下列关于区间估计的说法，正确的是
    A

    在进行区间估计时，置信区问的长度和估计的精度成正比

    B

    在进行区间估计时，置信区间的长度和估计的精度成反比

    C

    在进行区间估计时，置信概率和估计的可靠程度成反比

    D

    在进行区间估计时，估计的可靠程度和精确程度是无关的


    正确答案： D
    解析：

  • 第13题：

    将积分区间[a,b]分成若干小区间,在每个小区间上用低阶求积公式计算,然后将它们加起来,这就是复化求积方法。()


    参考答案：正确

  • 第14题：

    设[θL, θU]是θ的置信水平为1-a的置信区间，则有（ ）。
    A.a愈大，置信区间长度愈短 B.a愈大，置信区间长度愈长
    C.a愈小，置信区间包含θ的概率愈大 D.a愈小，置信区间包含θ的概率愈小
    E.置信区间长度与a大小无关


    答案：A,C
    解析：
    1-a置信区间的含义是：所构造的随机区间[θL, θU]覆盖（盖住）未知参数θ的概率为1-a。a愈大，区间[θL, θU]盖住未知参数θ的概率越小，区间的长度越短；a愈小，区间[θL, θU]盖住未知参数θ的概率越大，置信区间的长度越长。

  • 第15题：

    下列函数在区间[0，3]上不满足拉格朗日定理条件的是（ ）《》（ ）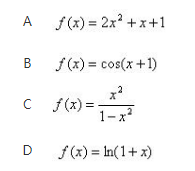


    答案：C
    解析：

  • 第16题：

    函数y=sinx在区间[0，π]上满足罗尔定理的ξ=（　　）


    答案：C
    解析：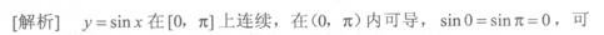

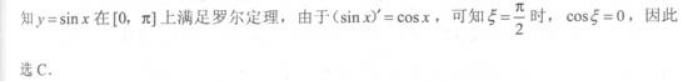
  • 第17题：

    双区间闭塞法行车时，列车占用区间的凭证为（），凭助理行车值班员手信号发车。追踪运行列车间的安全间隔按双区间要求，由双区间闭塞设备实现。


    正确答案:出站信号机的绿灯显示

  • 第18题：

    在其他条件不变的情形下，总体均值的的1-置信（）。

    • A、区间越大，长度越大
    • B、区间越大，长度越小
    • C、区间越小，长度越小
    • D、与长度没有关系

    正确答案:B

  • 第19题：

    困难区间就是限制区间。


    正确答案:错误

  • 第20题：

    区间估计是用多个区间来对未知数进行估计， 区间估计体现了估计的精度。


    正确答案:错误

  • 第21题：

    判断题
    区间估计是用多个区间来对未知数进行估计， 区间估计体现了估计的精度。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第22题：

    判断题
    困难区间就是限制区间。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第23题：

    多选题
    设[θL，θU]是θ的置信水平为1-α的置信区间，则有（　　）。[2006年真题]
    A

    α愈大，置信区间长度愈短

    B

    α愈大，置信区间长度愈长

    C

    α愈小，置信区间包含θ的概率愈大

    D

    α愈小，置信区间包含θ的概率愈小

    E

    置信区间长度与α大小无关


    正确答案： E,A
    解析：
    1-α置信区间的含义是：所构造的随机区间[θL，θU]覆盖（盖住）未知参数θ的概率为1-α。α愈大，区间[θL，θU]盖住未知参数θ的概率越小，区间的长度越短；α愈小，区间[θL，θU]盖住未知参数θ的概率越大，置信区间的长度越长。

  • 第24题：

    问答题
    设f（x）在闭区间[0，c]上连续，其导数f′（x）在开区间（0，c）内存在且单调减少，f（0）＝0，试应用拉格朗日中值定理证明不等式：f（a＋b）≤f（a）＋f（b），其中a，b满足条件0≤a≤b≤a＋b≤c。

    正确答案：
    f(a+b)-f(a)-f(b)=[f(a+b)-f(b)]-[f(a)-f(0)]。
    因为f(x)在区间(0,a),(b,a+b)上满足拉格朗日中值定理,因此分别存在ξ∈(0,a),η∈(b,a+b),使得f(a)-f(0)=af′(ξ),f(a+b)-f(b)=af′(η),从而有f(a+b)-f(a)-f(b)=a[f′(η)-f′(ξ)]。
    又f′(x)在(0,c)上单调减少,故f′(η)≤f′(ξ),故f(a+b)-f(a)-f(b)≤0,即f(a+b)≤f(a)+f(b)。
    解析： 暂无解析

相关内容