在定义域上处处可导的周期函数的导函数（）.A．不是周期函数B．是周期函数，但周期不一定与原函数的周期相同C．不一定是周期函数D．是周期函数，且周期与原函数的周期相同

题目

在定义域上处处可导的周期函数的导函数（）.

A．不是周期函数

B．是周期函数，但周期不一定与原函数的周期相同

C．不一定是周期函数

D．是周期函数，且周期与原函数的周期相同

相似考题

1.下列命题中正确的是()。A.连续函数必可导B.可导函数必连续C.函数可导的充要条件是函数连续D.存在极限的函数连续

2.周期函数的自相关函数仍然为同频率的周期函数。()

3.可导的周期函数的导函数还是周期函数。()此题为判断题(对，错)。

4.关于可导性,下列说法正确的是()。A、在区间上都是可导的B、在区间上都不可导C、在区间上除外都是可导的D、以上说法都不对

参考答案和解析
错误
更多“在定义域上处处可导的周期函数的导函数（）.”相关问题

  • 第1题：

    区间[a,b]上的三次样条插值函数是()

    A、在[a,b]上2阶可导，节点的函数值已知，子区间上为3次多项式

    B、在区间[a,b]上连续的函数

    C、在区间[a,b]上每点可微的函数

    D、在每个子区间上可微的多项式


    参考答案：A

  • 第2题：

    若f（x）是在（-∞，+∞）内可导的以l为周期的周期函数，则f′（ax+b）（a≠0，a、b为常数）的周期为（ ）

    A.l
    B.l-b
    C.l/a
    D.l/|a|

    答案：D
    解析：

  • 第3题：

    函数



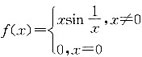
    在x=0处( )。

    A.连续，且可导
    B.连续，不可导
    C.不连续
    D.不仅可导，导数也连续

    答案：B
    解析：
    利用可导与连续的基本慨念即可得解

  • 第4题：

    下列函数中在x=0处可导的是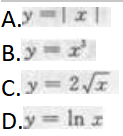


    答案：B
    解析：

  • 第5题：

    设f(x)是连续函数，
    　　(Ⅰ)利用定义证明函数可导，且F’(x)=f(x)；
    　　(Ⅱ)当f(x)是以2为周期的周期函数时，证明函数也是以2为周期的周期函数.


    答案：
    解析：



  • 第6题：

    (Ⅰ)证明拉格朗日中值定理：若函数f(x)在［a，b］上连续，在(a，b)内可导，则存在ξ∈(a，b)，使得f(b)-f(a)=f'(ξ)(b-a)；(Ⅱ)证明：若函数f(x)在x=0处连续，在(0，δ)(δ>0)内可导，且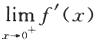=A，则存在，且.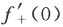


    答案：
    解析：

  • 第7题：

    下列函数在χ=0处可导的是( )。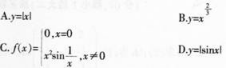


    答案：C
    解析：

  • 第8题：

    下列函数在x=0处可导的是( )。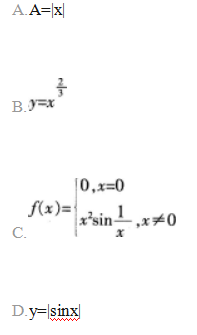


    答案：C
    解析：

  • 第9题：

    函数y=x+x｜x｜，在x=0处应：（）

    • A、连续且可导
    • B、连续但不可导
    • C、不连续
    • D、以上均不对

    正确答案:A

  • 第10题：

    可微函数若是单调增的，则（）。

    • A、函数大于0
    • B、其二阶导函数大于0
    • C、其导函数大于0
    • D、其二阶导函数小于0

    正确答案:C

  • 第11题：

    单选题
    二阶可微函数若是凸的，则（）。
    A

    其导函数小于0

    B

    其二阶导函数大于0

    C

    其导函数大于0

    D

    其二阶导函数小于0


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    若f（x）是在（－∞，＋∞）内可导的以l为周期的周期函数，则f′（ax＋b）（a≠0，a、b为常数）的周期为（　　）。
    A

    l

    B

    l－b

    C

    l/a

    D

    l/｜a｜


    正确答案： A
    解析：
    f（x）与f′（x）具有相同的周期。由f（x）的周期为l，可以推知f（ax＋b）的周期为l/｜a｜，故f′（ax＋b）的周期也是l/｜a｜。

  • 第13题：


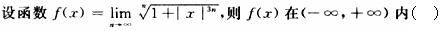    A.处处可导
    B.恰有一个不可导点
    C.恰有两个不可导点
    D.至少有三个不可导点

    答案：C
    解析：

  • 第14题：


    A.是周期函数，且周期为π
    B.是周期函数，且周期为2π
    C.是周期函数，且周期为3π
    D.不是周期函数

    答案：B
    解析：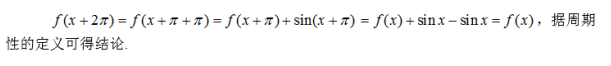

  • 第15题：

    函数：y=sin1/x在定义域内是：
    A.单调函数 B.周期函数
    C.无界函数 D.有界函数


    答案：D
    解析：
    提示:利用sin(1/x)的图形或取绝对值 sin(1/x) ≤1确定。

  • 第16题：

    函数y=｜x｜+1在x=0处()

    A.无定义
    B.不连续
    C.连续但是不可导
    D.可导

    答案：C
    解析：
    【考情点拨】本题考查了函数在一点可导、连续的性质的知识点．【应试指导】从四个选项的内容来看，我们可以一步一步地处理，x=0时，y=1，

  • 第17题：

    设函数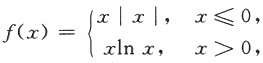则x=0是f(x)的

    A.A可导点，极值点B
    B.不可导点，极值点
    C.可导点，非极值点
    D.不可导点，非极值点

    答案：B
    解析：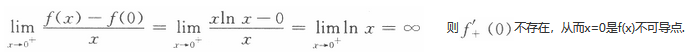

    又在x=0的左半邻域f(x)=x｜x｜<0=f(0)，
    　　在x=0的右半邻域f(x)=xln x<0=f(0)，
    　　则f(x)在x=0处取极大值，故应选(B).

  • 第18题：


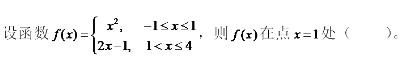    A.可导但导函数不连续
    B.可导且导函数连续
    C.连续但不可导
    D.不连续

    答案：B
    解析：

  • 第19题：

    若函数f(x)在[0，1]上黎曼可积，则f(x)在[0，1]上（ ）。

    A.连续
    B.单调
    C.可导
    D.有界

    答案：D
    解析：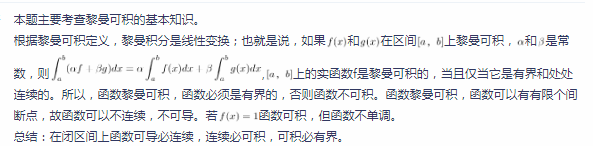

  • 第20题：


    A.非阶梯间断函数
    B.阶梯函数
    C.可导函数
    D.连续但不一定可导的函数

    答案：D
    解析：
    由连续随机变量密度函数可积，知分布函数连续。

  • 第21题：

    二阶可微函数若是凸的，则（）。

    • A、其导函数小于0
    • B、其二阶导函数大于0
    • C、其导函数大于0
    • D、其二阶导函数小于0

    正确答案:D

  • 第22题：

    设函数f(x)=丨x丨，则函数在点x=0处（）

    • A、连续且可导
    • B、连续且可微
    • C、连续不可导
    • D、不可连续不可微

    正确答案:C

  • 第23题：

    单选题
    设函数f(x)=丨x丨，则函数在点x=0处（）
    A

    连续且可导

    B

    连续且可微

    C

    连续不可导

    D

    不可连续不可微


    正确答案： C
    解析： 暂无解析

  • 第24题：

    单选题
    可微函数若是单调增的，则（）。
    A

    函数大于0

    B

    其二阶导函数大于0

    C

    其导函数大于0

    D

    其二阶导函数小于0


    正确答案： D
    解析： 暂无解析

相关内容