根据最小二乘法拟合直线回归方程是使（ ）。

题目
根据最小二乘法拟合直线回归方程是使（ ）。


相似考题

1.用最小二乘法以利润率为因变量拟合直线回归方程，其最小二乘法的原理是使（ ）。A．实际Y值与理论 值的离差和最小B．实际Y值与理论 值的离差平方和最小C．实际Y值与Y平均值的离差和最小D．实际Y值与Y平均值的离差平方和最小

2.在直线回归分析中，根据最小二乘法求得两条直线回归方程 和 。一般情况下，它们之间的关系是A、交叉B、重合C、交叉或重合D、平行E、平行或重合

3.按最小二乘法估计回归方程中参数的实质是使( )。A．B．C．D．

4.最小二乘法确定直线回归方程的基本原则是使各观察点A、距直线的纵向距离相等B、距直线的纵向距离的平方和最小C、与直线的垂直距离相等D、与直线的垂直距离的平方和最小E、距直线的纵向距离和的平方最小

更多“根据最小二乘法拟合直线回归方程是使（ ）。 ”相关问题

  • 第1题：

    线性回归是对任意两个数量指标进行线性拟合获得最佳直线回归方程，从而对该指标进行预测。（ ）


    正确答案：×
    线性回归是对两个具有相关关系的数量指标进行线性拟合获得最佳直线回归方程，从而在相关分析的基础上进行回归分析，且相关程度越高，回归测定的结果越可靠

  • 第2题：

    在直线回归分析中，根据最小二乘法求得两条直线回归方程＝a＋bx和＝c＋dy。一般情况下，它们之间的关系是

    A、交叉

    B、重合

    C、交叉或重合

    D、平行

    E、平行或重合


    参考答案：E

  • 第3题：

    根据最小二乘法拟合的趋势回归方程为：Tt= 112.67+0.698t，R2＝0.944，说明（ ）。

    A.该回归方程的拟合效果较好

    B.该回归方程的拟合效果较差

    C.该方程对变量的解释程度为94.4%

    D.时间每增加一个单位，T增加0.698个单位

    E.时间每增加一个单位，T平均增加0.698个单位


    正确答案：ACE

  • 第4题：

    用最小二乘法以利润率为因变量拟合直线回归方程，其最小二乘法的原理是使( )。

    A．实际Y值与理论Y值的离差和最小

    B．实际Y值与理论Y值的离差平方和最小

    C．实际Y值与Y平均值的离差和最小

    D．实际Y值与Y平均值的离差平方和最小


    正确答案：B
    解析：最小二乘法估计回归方程中参数的原理是：每一个指标实测值与指标理论值的离差平方和最小，即Q(β0，β1)=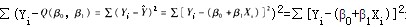最小。

  • 第5题：

    现有八家百货公司，每个公司人均月销售额和利润率资料如表5—3所示。



    用最小二乘法以利润率为因变量拟合直线回归方程，其最小二乘法的原理是使（）。



    答案：B
    解析：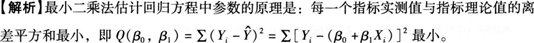

  • 第6题：

    用最小二乘法确定直线回归方程的原则是各观察点与直线的纵向距离的平方和最小。


    正确答案:正确

  • 第7题：

    根据下列资料编制直线回归方程r=0.9a=2.8（）

    • A、直线回归方程yc=2.8+1.08x
    • B、直线回归方程yc=2.8+1.18x
    • C、直线回归方程yc=0.9+1.08x
    • D、直线回归方程yc=0.9+1.18x

    正确答案:A

  • 第8题：

    最小二乘法作为一种数据处理手段，如用于求解一元线性回归方程的系数，应使各测量值与回归直线上相应值的（）最小。


    正确答案:偏差的平方和

  • 第9题：

    判断题
    最小二乘法的基本原理是：在所有拟合的直线中，与所测实际数据的偏差平方和最大的那条直线为最优
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第10题：

    填空题
    最小二乘法作为一种数据处理手段，如用于求解一元线性回归方程的系数，应使各测量值与回归直线上相应值的（）最小。

    正确答案： 偏差的平方和
    解析： 暂无解析

  • 第11题：

    单选题
    最小二乘法确定直线回归方程的基本原则是使各观察点（）
    A

    距直线的纵向距离相等

    B

    距直线的纵向距离的平方和最小

    C

    与直线的垂直距离相等

    D

    与直线的垂直距离的平方和最小

    E

    距直线纵向和垂直距离均相等


    正确答案： B
    解析： 用最小二乘法确定直线回归方程的原则是各观察点与直线的垂直距离的平方和最小。

  • 第12题：

    单选题
    在直线回归分析中，根据最小二乘法求得两条直线回归方程和。一般情况下，它们之间的关系是（）
    A

    交叉

    B

    重合

    C

    交叉或重合

    D

    平行

    E

    平行或重合


    正确答案： E
    解析： 在直线回归分析中，根据最小二乘法求得两条直线回归方程。一般情况下，它们之间的关系是交叉或重合。

  • 第13题：

    基于“使残差的平方和”为最小的准则来选取拟合曲线的方法称为曲线拟合的最小二乘法。()


    参考答案：√

  • 第14题：

    最小二乘法确定直线回归方程的基本原则是使各观察点

    A．距直线的纵向距离相等

    B．距直线的纵向距离的平方和最小

    C．与直线的垂直距离相等

    D．与直线的垂直距离的平方和最小

    E．以上均不对


    正确答案：B

  • 第15题：

    用最小二乘法拟合回归直线方程，其基本原理是（ ）。


    正确答案：D

  • 第16题：

    相关分析是对两具有相关关系的数量指标进行线性拟合获得最佳直线回归方程，从而对该指标进行预测。（）


    答案：错
    解析：
    一元线性回归是对两个具有相差关系的数量指标进行线性拟合获得最佳直线回归方程，从而在相关分析的基础上连行指标预测。

  • 第17题：

    拟合直线回归方程yc=a+bx有什么要求？其参数a、b的经济涵义是什么？
    拟合直线回归方程的要求是：找到合适的参数a、b，使所确定的回归方程能够做到；实际的y值与对应的理论值yc的离差平方和为最小值。即：Q=∑（y-yc）2=∑（y-a-bx）2=最小值。按此要求配合的酬归方程，比用其他方法配合的回归方程的代表性要高。回归方程中参数a代表直线的起点值，在数学上称为直线的纵轴截距；参数b称为回归系数，表示自变量增加一个单位时因变量的平均增加值。
    略

  • 第18题：

    要想使直线回归方程式y=a+bx与实际情况拟合得最好，就必须使（）

    • A、总偏差平方和最小
    • B、正、负误差之和最小
    • C、误差绝对值之和最小
    • D、误差平方和最小

    正确答案:D

  • 第19题：

    最小二乘法的基本原理是：在所有拟合的直线中，与所测实际数据的偏差平方和最大的那条直线为最优


    正确答案:正确

  • 第20题：

    利用最小二乘法的原理配合的直线回归方程，要求实际测定值的所有相关点到直线上的距离平方和等于0。


    正确答案:正确

  • 第21题：

    多选题
    确定拟合直线的方法有（）。
    A

    端基直线法

    B

    拟合曲线法

    C

    校准曲线法

    D

    最小二乘法


    正确答案： A,B
    解析： 暂无解析

  • 第22题：

    填空题
    最小二乘法的原理是要是直线拟合得更好，应使（）为最小。

    正确答案： 残差平方和
    解析： 暂无解析

  • 第23题：

    问答题
    拟合直线回归方程yc=a+bx有什么要求？其参数a、b的经济涵义是什么？

    正确答案： 拟合直线回归方程的要求是：找到合适的参数a、b，使所确定的回归方程能够做到；实际的y值与对应的理论值yc的离差平方和为最小值。即：Q=∑（y-yc）2=∑（y-a-bx）2=最小值。按此要求配合的酬归方程，比用其他方法配合的回归方程的代表性要高。回归方程中参数a代表直线的起点值，在数学上称为直线的纵轴截距；参数b称为回归系数，表示自变量增加一个单位时因变量的平均增加值。
    解析： 暂无解析

相关内容