设α1，α2，α3，α4 是三维实向量，则（ ）A. α1，α2，α3，α4一定线性无关 B. α1一定可由α2，α3，α4线性表出C. α1，α2，α3，α4一定线性相关 D. α1，α2，α3一定线性无关

题目

设α1，α2，α3，α4 是三维实向量，则（ ）

A. α1，α2，α3，α4一定线性无关 B. α1一定可由α2，α3，α4线性表出

C. α1，α2，α3，α4一定线性相关 D. α1，α2，α3一定线性无关

相似考题

1.设a1,a2,a3,a4,a5是四维向量,则()A、a1，a2，a3，a4，a5一定线性无关B、a1，a2，a3，a4，a5一定线性相关C、a5一定可以由a1，a2，a3，a4线性表示D、a1一定可以由a2，a3，a4，a5线性表出

2.设向量组α1=（1，2，3，6），α2=（1，-1，2，4），α3=（-1，1，-2，-8），α4=（1，2，3，2）.（1）求该向量组的一个极大线性无关组；

3.已知向量组α1,α2，α3，α4线性无关，证明：α1+α2，α2+α3，α3+α4，α4-α1线性无关.

4.设向量组a1,a2,a3线性无关,则下列向量组中线性无关的是()。A、a1-a2,a2-a3,a3-a1B、a1,a2,a3+a1C、a1,a2,2a1-3a2D、a2,a3,2a2+a3

参考答案和解析
正确答案：C
更多“设α1,α2,α3,α4 是三维实向量,则( )A. α1,α2,α3,α4一定线性无关 B. α1一定可由α2,α3,α4线性表出 ”相关问题

  • 第1题：

    设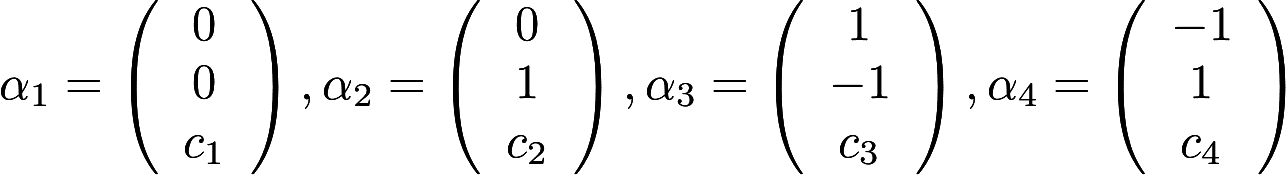其中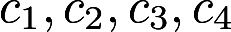为任意常数，则下列向量组线性相关的是（ ）

    A.a1，a2，a3
    B.a1，a2，a4
    C.a1，a3，a4
    D.a2，a3，a4

    答案：C
    解析：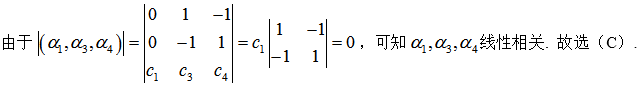

  • 第2题：

    已知4阶方阵A=（α1, α2, α3,α4)，其中α1, α2, α3,α4均为4维的列向量，且α2, α3, α4线性无关，α1 = 2α2- α3，如果β = α1 + α2 + α4，求线性方程组Ax = β的通解.


    由题意可知，因为α 2 ,α 3 ,α 4 ，线性无关且α 1 =2α 2 -α 3 +0α4]则可知．r(A)=3，从而Ax=0的基础解系含4-r(A)=4-3＝1个解向量．由α 1 -2α 2 +α 3 +0α 4 =0)知(1,-2,1,0) T 是Ax=0的非零解，故可作为Ax=0的一个基础解系，所以Ax=β的一个特解为(1,1,1,1) T ，故Ax=β的通解可表示为x=(1,1,1,1) T +k(1,-2,1,0) T (k为任意常数) [逻辑推理] 首先根据所给条件确定A的秩，从而求出Ax=0的基础解系，再找出Ax=β的一个特解，从而得到Ax=β的通解．

  • 第3题：

    向量组 a=（1,2,3),b=（4,1,0),c=（1,-1,5)线性无关，则向量组a1=（2,1,3),b1=（1,4,0), c1=（-1,1,5)线性无关


    线性无关

  • 第4题：

    若向量组α1，α2，α3，α4，α5线性相关，α1，α2，α3线性无关，则矩阵A=（α1，α2，α3，α4，α5)的秩R（A)____.

    A．R(A)＞3

    B．R(A)≤5

    C．3＜R(A)＜5

    D．3≤R(A)＜5


    C 注意到所给向量组α1，α2，α3中向量的维数等于向量的个数，因此计算矩阵A＝(α1，α2，α3)的行列式｜A｜，有由于向量α1，α2，α3线性相关，因而行列式｜A｜＝0，即λ＋1＝0，于是分量λ＝－1这个正确答案恰好就是备选答案C，所以选择C．

  • 第5题：

    求向量组（2,1,4,3), （-1,1,-6,6), （-1,-2,2,-9), （1,1,-2,7), （2,4,4,9)的秩并判断其是否线性相关：

    A．3，线性相关

    B．2，线性相关

    C．2，线性无关

    D．3，线性无关


    D

相关内容