两个二元函数在一点处一个存在极限，一个不存在极限，那么它们的和在该点处极限不存在

题目

两个二元函数在一点处一个存在极限，一个不存在极限，那么它们的和在该点处极限不存在

相似考题

1.函数在一点处极限存在的充要条件是函数在该点的左极限等于右极限。()此题为判断题(对，错)。

2.函数在x→1时，f(x)的极限是： A.2 B.3 C.0 D.不存在

3.函数y=f(x)在点x=x0处左右极限都存在并且相等，是它在该点有极限的（）A.必要条件 B.充分条件 C.充要条件 D.无关条件

4.A.极限不存在 B.极限存在但不连续 C.连续但不可导 D.可导

更多“两个二元函数在一点处一个存在极限，一个不存在极限，那么它们的和在该点处极限不存在”相关问题

  • 第1题：

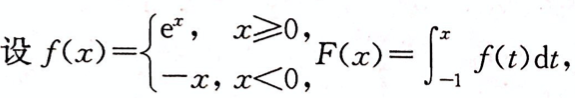    则F（x)在x=0处

    A. 极限不存在
    B. 极限存在但不连续
    C. 连续但不可导
    D. 可导

    答案：C
    解析：

  • 第2题：

    直流输电不存在稳定极限问题，是提高线路输电容量的一个重要途径。（ ）


    答案：对
    解析：
    随着距离的增加、电压等级的升高，远距离输电造成的线损也不断增加。而直流输电方式因其不存在稳定极限问题，成为提高线路输送容量的一个重要途径，并且可以减少电网间互联，限制故障范围，提高稳定性水平。

  • 第3题：

    设其中g(x)是有界函数，则f(x)在x=0点( )。

    A、极限不存在
    B、极限存在但不连续
    C、连续、但不可导
    D、可导

    答案：D
    解析：

  • 第4题：

    函数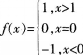x=0点( )。

    A、极限存在，且等于O
    B、左、右极限存在，但极限不存在
    C、左极限存在，但右极限不存在
    D、左极限不存在，但右极限存在

    答案：B
    解析：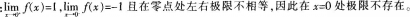

  • 第5题：

    设f（x)为不恒等于零的奇函数，且厂(0)存在，则函数()。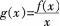

    A、在x=0处左极限不存在
    B、有跳跃间断点x=0
    C、在x=0处右极限不存在
    D、有可去间断点x=0

    答案：D
    解析：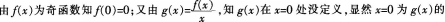

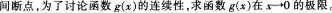
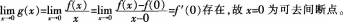
  • 第6题：

    只存在结构承载能力的极限状态，结构的正常使用不存在极限状态。

    A对

    B错


    错
    略

  • 第7题：

    在间断点处，函数肯定没有极限。


    正确答案:错误

  • 第8题：

    若x点是函数的可去间断点，则在x点处函数（）。

    • A、左右极限都存在但不相等
    • B、左极限不存在
    • C、左右极限都存在且相等
    • D、右极限不存在

    正确答案:C

  • 第9题：

    若x点是函数的第二类间断点，则在x点处函数（）。

    • A、极限值不等于这点的函数值
    • B、左右极限都存在
    • C、左右极限至少有一个不存在
    • D、没有定义

    正确答案:C

  • 第10题：

    单选题
    若x点是函数的第二类间断点，则在x点处函数（）。
    A

    极限值不等于这点的函数值

    B

    左右极限都存在

    C

    左右极限至少有一个不存在

    D

    没有定义


    正确答案： C
    解析： 暂无解析

  • 第11题：

    单选题
    二元函数的极限与累次极限之间的关系是（）。
    A

    二元函数的极限存在则两累次极限都存在

    B

    累次极限就是二元函数的极限

    C

    两累次极限都存在则二元函数的极限存在

    D

    二元函数的极限和两累次极限都存在时，可用累次极限求二元函数极限


    正确答案： A
    解析： 暂无解析

  • 第12题：

    判断题
    只存在结构承载能力的极限状态，结构的正常使用不存在极限状态。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第13题：

    函数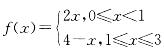在x→1时，f(x)的极限是：

    A.2
    B.3
    C.0
    D.不存在

    答案：D
    解析：
    提示:计算f(x)在x=1的左、右极限：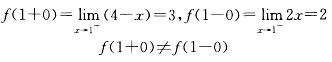

  • 第14题：

    函数y=f（x）在点xo处的左、右极限存在且相等是函数在该点极限存在的（ ）.《》（ ）

    A.必要条件
    B.充分条件
    C.充分必要条件
    D.既非充分条件，也非必要条件

    答案：C
    解析：

  • 第15题：

    函数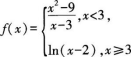在x=3处的极限是( )


    A.不存在

    B.等于6

    C.等于3

    D.等于0

    答案：A
    解析：
    分段函数在x=3处不是无限靠近同一个值，故不存在极限。

  • 第16题：


    A、极限不存在
    B、极限存在但不连续
    C、连续，但不可导
    D、可导

    答案：D
    解析：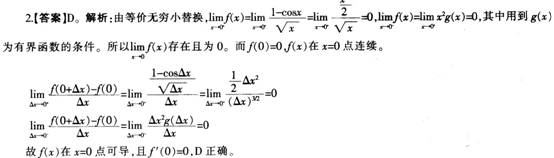

  • 第17题：

    求极限时，下列各种解法中正确的是（ ）。
    A.用洛必达法则后，求得极限为0
    B.因为不存在，所以上述极限不存在
    C.
    D.因为不能用洛必达法则，故极限不存在


    答案：C
    解析：

  • 第18题：

    只存在结构承载能力的极限状态，结构的正常使用不存在极限状态。


    正确答案:错误

  • 第19题：

    函数在某一点处的导数是一种无穷小比无穷小的极限。


    正确答案:正确

  • 第20题：

    二元函数的极限与累次极限之间的关系是（）。

    • A、二元函数的极限存在则两累次极限都存在
    • B、累次极限就是二元函数的极限
    • C、两累次极限都存在则二元函数的极限存在
    • D、二元函数的极限和两累次极限都存在时，可用累次极限求二元函数极限

    正确答案:D

  • 第21题：

    函数在一点处的左右极限都存在，则函数在这一点的极限存在。


    正确答案:错误

  • 第22题：

    单选题
    若x点是函数的可去间断点，则在x点处函数（）。
    A

    左右极限都存在但不相等

    B

    左极限不存在

    C

    左右极限都存在且相等

    D

    右极限不存在


    正确答案： A
    解析： 暂无解析

  • 第23题：

    判断题
    函数在某一点处的导数是一种无穷小比无穷小的极限。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第24题：

    判断题
    函数在一点处的左右极限都存在，则函数在这一点的极限存在。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

相关内容