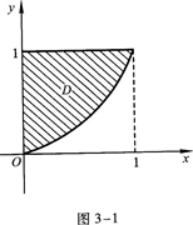
求由曲线y=x2(x≥0)，直线y=1及Y轴围成的平面图形的面积·

题目
求由曲线y=x2(x≥0)，直线y=1及Y轴围成的平面图形的面积·

相似考题

1.已知曲线C为y= 2x2，直线l为y= 4x．（10分）(1)求由曲线C与直线l所围成的平面图形的面积S；(2)求过曲线C且平行于直线l的切线方程．

2.求由曲线y=ex，y=e-x及x=1所围成的平面图形的面积以及此平面图形绕x轴旋转一周所成的旋转体的体积Vx.

3.求曲线y=2-x2和直线y=2x＋2所围成图形面积．

4.曲线y=x2与y=4—x2所围成的图形的面积为_________．

更多“求由曲线y=x2(x≥0)，直线y=1及Y轴围成的平面图形的面积· ”相关问题

  • 第1题：

    由曲线y=ex，y=e-2x及直线x=-1所围成图形的面积是：


    答案：B
    解析：
    提示：画图分析围成平面区域的曲线位置关系，得到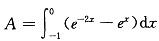计算出结果。

  • 第2题：

    求曲线y=x2与该曲线在x=a(a>0)处的切线与x轴所围的平面图形的面积．


    答案：
    解析：

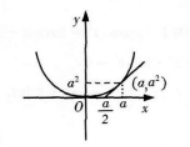
    即y=2ax-a2，


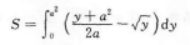
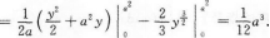
  • 第3题：

    已知曲线C为y=2x2及直线L为y=4x．
    ①求由曲线C与直线L所围成的平面图形的面积S；
    ②求曲线C的平行于直线L的切线方程．


    答案：
    解析：
    画出平面图形如图l一3—4阴影所示．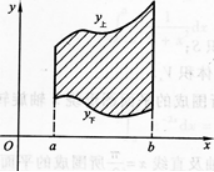
    图1—3—3

    图1—3—4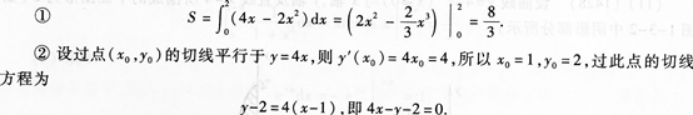

  • 第4题：

    ①求曲线y=x2(x≥0)，y=1与x=0所围成的平面图形的面积S：
    ②求①中的平面图形绕Y轴旋转一周所得旋转体的体积Vy．


    答案：
    解析：
    ①由已知条件画出平面图形如图l—3-5阴影所示．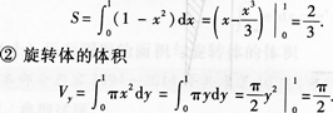

    图1—3—5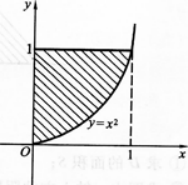

  • 第5题：

    由曲线y=x3，直线x=1，z轴围成的平面有界区域的面积为_________．


    答案：
    解析：
    【答案】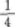
    【考情点拨】本题考查了积分的应用的知识点．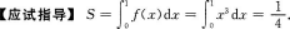

  • 第6题：

    求曲线y=x2与直线y=0，x=1所围成的平面图形绕x轴旋转一周所得旋转体的体积．


    答案：
    解析：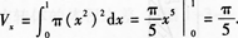

  • 第7题：

    设非负函数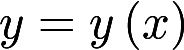满足微分方程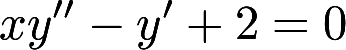，当曲线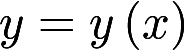过原点时，其与直线x=1及y=0围成平面区域D的面积为2，求D绕y轴旋转所得旋转体的体积


    答案：
    解析：

  • 第8题：

    曲线y=sinx(0≤x≤π/2)与直线x=π/2,y=0围成的平面图形绕x轴旋转产生的旋转体体积是()。


    答案：A
    解析：
    提示：利用旋转体体积公式

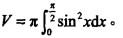
  • 第9题：

    设l是曲线y=x2+3在点(1，4)处的切线，求由该曲线，切线l及Y轴围成的平面图形的面积S．


    答案：
    解析：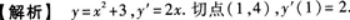
    故切线l的方程为y=2x+2．

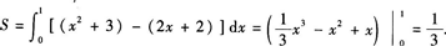
  • 第10题：

    由曲线y=x2，直线y=a，x=0及x=1所围成的图形如图3—4中阴影部分所示，其中0≤a≤1．

    (1)求图中阴影部分的面积A．
    (2)问a为何值时，A的取值最小，并求出此最小值．


    答案：
    解析：

  • 第11题：

    已知曲线y=ex与直线y=c(c>1)及Y轴所围成的平面图形的面积为1，求实数c的值。


    答案：
    解析：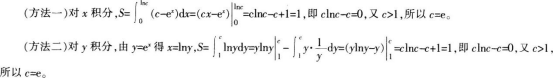

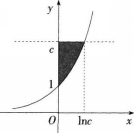
  • 第12题：

    单选题
    由抛物线y=x2与三直线x=a，x=a+1，y=0围成平面图形。问a为何值时图形的面积最小？（）
    A

    1

    B

    -1／2

    C

    0

    D

    2


    正确答案： D
    解析： 暂无解析

  • 第13题：

    由抛物线y=x2与三直线x=a，x=a+1，y=0所围成的平面图形，a为下列（　　）值时图形的面积最小。


    答案：B
    解析：
    平面图形的面积

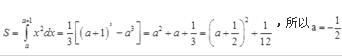
    时图形面积最小。

  • 第14题：

    设曲线y=4-x2(x≥0)与x轴，y轴及直线x=4所围成的平面图形为D(如
    图1—3—2中阴影部分所示)．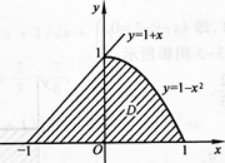

    图1—3—1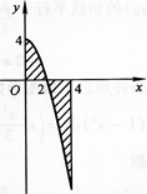

    图1—3—2
    ①求D的面积S；
    ②求图中x轴上方的阴影部分绕y轴旋转一周所得旋转体的体积Vy．


    答案：
    解析：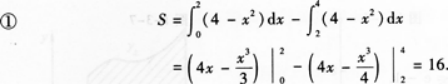

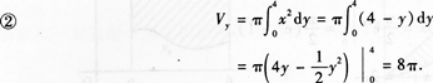
  • 第15题：

    ①求由曲线y=x，y=1/x，x=2与y=0所围成的平面图形的面积S；
    ②求①中的平面图形绕x轴旋转一周所得旋转体的体积V．


    答案：
    解析：
    ①如图1—3-6所示，由已知条件可得

  • 第16题：

    设D为曲线y=1-x2，直线y=x+1及x轴所围成的平面区域(如图1-3—1所示)·
    ①求平面图形的面积；
    ②求平面图形D绕x轴旋转一周所成旋转体的体积Vx．


    答案：
    解析：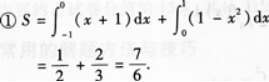

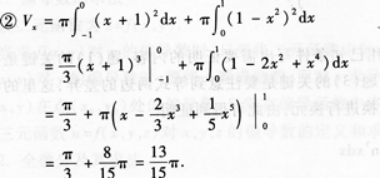
  • 第17题：

    ①求曲线y=ex及直线x=1，x=0，y=0所围成的图形D的面积S：
    ②求平面图形D绕x轴旋转一周所成旋转体的体积Vx．


    答案：
    解析：
    画出平面图形如图l一3-7阴影所示．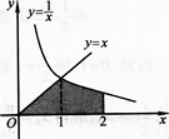
    图1—3—6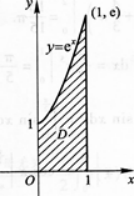

    图1—3—7

  • 第18题：

    曲线Y=x2，x=0，x=2，Y=0所围成的图形的面积为（　　）．



    答案：B
    解析：
    如右图所示，阴影部分的面积即为所求，由定积分的几何


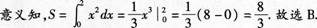
  • 第19题：



    (1)求f(x)和g(x)围成的平面区域的面积.?
    (2)求0≤y≤f(x), 1≤x≤3,绕y轴旋转的体积.?


    答案：
    解析：

  • 第20题：

    设曲线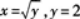及x=0所围成的平面图形为D．
    (1)求平面图形D的面积s．
    (2)求平面图形D绕y轴旋转一周生成的旋转体体积V


    答案：
    解析：
    平面图形D如图3-2所示．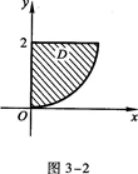
    (1)




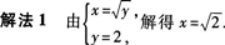
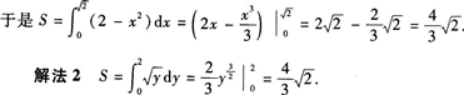
    (2)

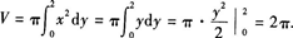
  • 第21题：

    设D为曲线y=x2与直线y=x所围成的有界平面图形，求D绕x轴旋转一周所得旋转体的体积V.?


    答案：
    解析：

  • 第22题：

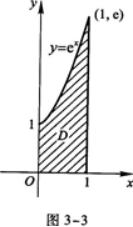
    (1)求曲线Y=ex及直线x=1，x=0,y=0所围成的平面图形(如图3—3所示)
    的面积A．
    (2)求(1)中平面图形绕x轴旋转一周所得旋转体的体积Vx.


    答案：
    解析：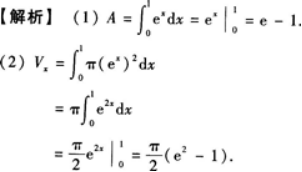

  • 第23题：

    由抛物线y=x2与三直线x=a，x=a+1，y=0围成平面图形。问a为何值时图形的面积最小？（）

    • A、1
    • B、-1／2
    • C、0
    • D、2

    正确答案:B

相关内容