设函数y=e2x，则y"(0)=_____．

题目
设函数y=e2x，则y"(0)=_____．

相似考题

1.设X、Y的联合分布函数是F(x,y),则F(＋∞,y)等于:()A、0;B、1;C、Y的分布函数;D、Y的密度函数。

2.设函数y=xex，则y"(O)=_________．

3.设函数y=sinx，则y"=_____．

4.设函数y=1/(1+cosx)，则y′=__________。

更多“设函数y=e2x，则y"(0)=_____．”相关问题

  • 第1题：

    若y=e2x，则dy=_________．


    答案：
    解析：
    【答案】2e2xdx【考情点拨】本题考查了微分的知识点．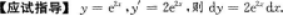

  • 第2题：

    设随机变量X～N(0,1),且y=9X^2,则y的密度函数为_______.


    答案：
    解析：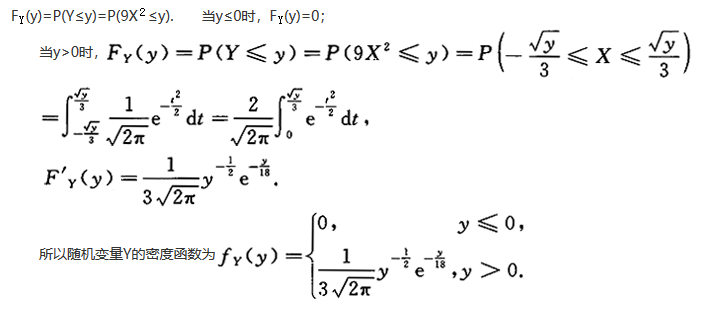

  • 第3题：

    求函数f(x，y)=e2x(x+y2+2y)的极值.?


    答案：
    解析：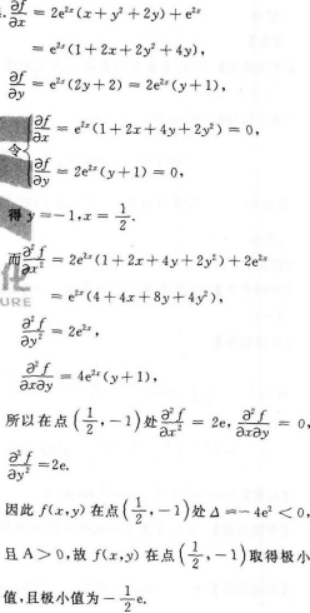

  • 第4题：

    填空题
    设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。

    正确答案： -1/7
    解析：
    由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
    又y（0）＝2，f′（2）＝1/2，f′（4）＝1，，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。

  • 第5题：

    单选题
    设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
    A

    1

    B

    2

    C

    3

    D

    4


    正确答案： B
    解析：
    ln（x2＋y）＝x3y＋sinx两边同时对x求导，得（2x＋y′）/（x2＋y）＝3x2y＋x3y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

  • 第6题：

    填空题
    设二元函数z＝xex＋y＋（x＋1）ln（1＋y），则dz|（1，0）＝____。

    正确答案： 2edx+(e+2)dy
    解析：
    由二元函数z＝xex＋y＋（x＋1）ln（1＋y）得∂z/∂x＝ex＋y＋xex＋y＋ln（1＋y），∂z/∂y＝xex＋y＋（x＋1）/（1＋y），故有∂z/∂x|（1，0）＝2e，∂z/∂y|（1，0）＝e＋2，dz|（1，0）＝2edx＋（e＋2）dy。

  • 第7题：

    问答题
    设二阶线性微分方程y″＋P（x）y′＋Q（x）y＝f（x）的三个特解是y1＝x，y2＝ex，y3＝e2x，试求此方程满足条件y（0）＝1，y′（0）＝3的特解。

    正确答案：
    由题意可知,Y1=ex-x、Y2=e2x-x是原方程对应齐次方程的两个线性无关的解[因(ex-x)/(e2x-x)≠常数],故原方程的通解为y=C1(ex-x)+C2(e2x-x)+x,由y(0)=1,y′(0)=3,得C1=-1,C2=2。故所求原方程的特解为y=-(ex-x)+2(e2x-x)+x=2e2x-ex。
    解析： 暂无解析

  • 第8题：

    单选题
    设f（x，y）与φ（x，y）均为可微函数，且φy′（x，y）≠0。已知（x0，y0）是f（x，y）在约束条件φ（x，y）＝0下的一个极值点，下列选项正确的是（　　）。
    A

    若fx′（x0，y0）＝0，则fy′（x0，y0）＝0

    B

    若fx′（x0，y0）＝0，则fy′（x0，y0）≠0

    C

    若fx′（x0，y0）≠0，则fy′（x0，y0）＝0

    D

    若fx′（x0，y0）≠0，则fy′（x0，y0）≠0


    正确答案： A
    解析：
    设z＝f（x，y）＝f（x，y（x）），由题意可知∂z/∂x＝fx′＋fy′·（dy/dx）＝0。
    又φ（x，y）＝0，则dy/dx＝－φx′/φy′。故fx′－（φx′/φy′）fy′＝0。又φy′≠0，则fx′φy′＝φx′fy′。所以当fx′≠0时fy′≠0。

  • 第9题：

    填空题
    设函数y＝y（x）由方程y＝1－xey确定，则（dy/dx）|x＝0＝____。

    正确答案： -e
    解析：
    设F（x，y）＝y－1＋xey，则dy/dx＝－Fx′/Fy′＝－ey/（1＋xey）。x＝0时，y＝1，代入上式得（dy/dx）|x＝0＝－e。

  • 第10题：

    填空题
    设函数y＝y（x）由方程exy＋ln[y/（x＋1）]＝0所确定，则y′（0）＝____。

    正确答案： (e-1)/e2
    解析：
    exy＋ln[y/（x＋1）]＝0方程两边对x求导，得exy（y＋xy′）＋y′/y－1/（x＋1）＝0。当x＝0时，y＝e－1。将x＝0，y＝e－1代入上式，得y′（0）＝（e－1）/e2。

  • 第11题：

    填空题
    设函数y＝1/（2x＋3），则y（n）（0）＝____。

    正确答案： (-1)n2nn!/3n+1
    解析：
    本题采用归纳法：y＝（2x＋3）－1，y′＝－2（2x＋3）－2，y″＝22·2（2x＋3）－3，y‴＝－23·3·2（2x＋3）－4，……
    ∴y（n）（x）＝（－1）n2n·n!/（2x＋3）n＋1，y（n）（0）＝（－1）n2nn!/3n＋1。

  • 第12题：

    单选题
    设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
    A

    0

    B

    1

    C

    2

    D

    e


    正确答案： B
    解析：
    ln（x2＋y）＝x3y＋sinx两边同时对x求导，得（2x＋y′）/（x2＋y）＝3x2y＋x3y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

  • 第13题：

    设函数y=sin(2x+1)，则y"=_____．


    答案：
    解析：
    填-4sin(2x+1)．

  • 第14题：

    设函数y(x)是微分方程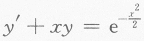满足条件y(0)=0的特解.
    　　(Ⅰ)求y(x)；
    　　(Ⅱ)求曲线y=y(x)的凹凸区间及拐点.


    答案：
    解析：

  • 第15题：

    设函数y＝e2xcos3x，则dy＝（）。

    • A、e2x（2cos3x-3sin3x）
    • B、e2x（2cos3x-3sin3x）dx
    • C、-6e2xsin3xdx
    • D、e2x（2cos3x+3sin3x）dx

    正确答案:B

  • 第16题：

    单选题
    设确定了函数y＝g（x），则（　　）。
    A

    x＝0是函数y＝g（x）的驻点，且是极大值点

    B

    x＝0是函数y＝g（x）的驻点，且是极小值点

    C

    x＝0不是函数y＝g（x）的驻点

    D

    存在x＝0的一个小邻域，y＝g（x）是单调的


    正确答案： A
    解析：
    g′（x）＝dy/dx＝（dy/dt）·（dt/dx）。dy/dt＝2t/（1＋t2），dx/dt＝1/（1＋t2）。故y′（x）＝2t。又x＝0时，t＝0，g′（x）＝0；t＜0时，x＜0，g′（x）＜0，g（x）单调减少；t＞0时，x＞0，g′（x）＞0，g（x）单调增加。故x＝0是y＝g（x）的驻点，且是极小值点。

  • 第17题：

    填空题
    设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝____。

    正确答案： 1
    解析：
    ln（x2＋y）＝x3y＋sinx两边同时对x求导，得（2x＋y′）/（x2＋y）＝3x2y＋x3y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

  • 第18题：

    单选题
    设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。
    A

    1

    B

    －1

    C

    1/7

    D

    －1/7


    正确答案： B
    解析：
    由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
    又y（0）＝2，f′（2）＝1/2，f′（4）＝1，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。

  • 第19题：

    单选题
    设z＝φ（x2－y2），其中φ有连续导数，则函数z满足（　　）。
    A

    x∂z/∂x＋y∂z/∂y＝0

    B

    x∂z/∂x－y∂z/∂y＝0

    C

    y∂z/∂x＋x∂z/∂y＝0

    D

    y∂z/∂x－x∂z/∂y＝0


    正确答案： D
    解析：
    令u＝x2－y2，则z＝φ（u），∂z/∂x＝φ′（u）·2x＝2xφ′（u），∂z/∂y＝－2yφ′（u），故y∂z/∂x＋x∂z/∂y＝0。

  • 第20题：

    单选题
    设y1＝e2x/2，y2＝exshx，y3＝exchx，则（　　）。
    A

    y1，y2，y3都没有相同的原函数

    B

    y2与y3有相同的原函数，但与y1的原函数不相同

    C

    y1，y2，y3有相同的原函数ex/（chx＋shx）

    D

    y1，y2，y3有相同的原函数ex/（chx－shx）


    正确答案： B
    解析：
    由于y1＝e2x/2，y2＝（e2x/2）－1/2，y3＝（e2x/2）＋1/2，故三个函数的原函数都不相同。

  • 第21题：

    填空题
    设f（x，y，z）＝exyz2，其中z＝z（x，y）是由x＋y＋z＋xyz＝0确定的隐函数，则fx′（0，1，－1）＝____。

    正确答案： 1
    解析：
    构造函数F（x，y，z）＝x＋y＋z＋xyz，则有∂z/∂x＝－Fx′/Fz′＝－（1＋yz）/（1＋xy），（∂z/∂x）|（0，1，－1）＝0，又由f（x，y，z）＝exyz2 ，得fx′＝exyz2＋exy·2z·zx′，代入（0，1，－1），得fx′（0，1，－1）＝e0×1×（－1）2＋e0×1×2×（－1）×0＝1。

  • 第22题：

    填空题
    设函数y＝y（x）由方程2xy＝x＋y所确定，则dy|x＝0＝____。

    正确答案： (ln2-1)dx
    解析：
    2xy＝x＋y等式两边求微分，得2xyln2d（xy）＝dx＋dy，即2xyln2（xdy＋ydx）＝dx＋dy。当x＝0时，y＝1，代入上式得dy|x＝0＝（ln2－1）dx。

  • 第23题：

    单选题
    设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
    A

    ln1

    B

    0

    C

    sin1

    D

    1


    正确答案： A
    解析：
    ln（x2＋y）＝x3y＋sinx两边同时对x求导，得（2x＋y′）/（x2＋y）＝3x2y＋x3y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

相关内容