设函数y=sinx，则y"=_____．

题目

相似考题

1.设X、Y的联合分布函数是F(x,y),则F(＋∞,y)等于:()A、0;B、1;C、Y的分布函数;D、Y的密度函数。

2.设函数y=xex，则y"(O)=_________．

3.设y=ln(1＋sinx),求y'。

4.设函数y=1/(1+cosx)，则y′=__________。

更多“设函数y=sinx，则y"=_____．”相关问题

第1题：

设y＝ln（sinx），则二阶导数y″等于（　　）。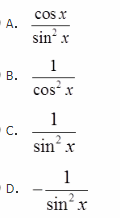

答案：D
解析：
函数y＝lnx，则y′＝1/x。因此，y＝ln（sinx）时，根据复合函数求导的链式法则，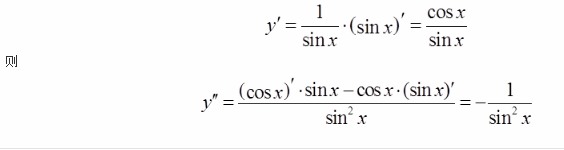
第2题：

设函数y=sinx2+2x，求dy．

答案：
解析：
y'=2xcosx2+2，则dy=2xcosx2+2)dx．
第3题：

设函数y=xsinx，则y"=_____．

答案：
解析：
填2cosx-xsinx．y'=sinx+xcosx，y"=cosx+cosx-xsinx=2cosx-xsinx·
第4题：

设(X,Y)的联合分布函数为F(x,y)=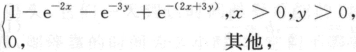则P(max{X,y}>1)=_______.

答案：
解析：
由Fx(x)=F(x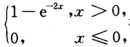，+∞)=得X～E(2)，同理Y～E(3)，且X,Y独立.P(max{X,Y}>1)=P(X>1Y>1)=1-P(X≤1,Y≤1)=1-P(X≤1)P(Y≤1)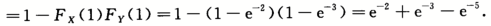
第5题：

下列函数在定义域内，既是奇函数又是增函数的是（）

A.y=sinx
B.y=log2x
C.y=x+8
D.y=x3

答案：D
解析：
第6题：

下列函数中，与函数定义域相同的函数为( )。
A．y=1/sinx
B．y=lnx/x
C．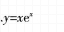
D．y=sinx/x

答案：D
解析：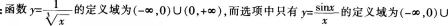
第7题：

设y=cosx，则y′′=( )

A.sinx
B.cosx
C.-cosx
D.-sinx

答案：C
解析：
【考情点拨】本题考查了函数的二阶导数的知识点.【应试指导】y=cosx，y'=-sinx，y''=-cosx.
第8题：

单选题
若∂2u/∂x∂y＝1，且当x＝0时，u＝siny，当y＝0时，u＝sinx，则u（x，y）＝（　　）。
A
xy＋sinx＋siny
B
－xy＋sinx＋siny
C
xy－sinx＋siny
D
xy＋sinx－siny

正确答案： A
解析：
u是x、y的二元函数，则∂²u/∂x∂y对y积分后应加一个关于x的函数，而不是常数C。即对∂²u/∂x∂y＝1两边对y积分得∂u/∂x＝y＋φ′（x），再两边对x积分得u（x，y）＝xy＋φ（x）＋ψ（y）。又x＝0时，u＝siny，得siny＝φ（0）＋ψ（y），即ψ（y）＝siny－φ（0）；又y＝0时，u＝sinx得sinx＝φ（x）＋ψ（0），令x＝0得φ（0）＋ψ（0）＝0。故u（x，y）＝xy＋sinx＋siny－φ（0）－ψ（0）＝xy＋sinx＋siny。
第9题：

填空题
设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝____。

正确答案： 1
解析：
ln（x²＋y）＝x³y＋sinx两边同时对x求导，得（2x＋y′）/（x²＋y）＝3x²y＋x³y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。
第10题：

填空题
设u＝sinx＋φ（sinx＋cosy）（φ为可微函数），且当x＝0时，u＝sin2y，则∂u/∂y＝____。

正确答案： 2(sinxsiny+cosysiny)
解析：
由于x＝0，u＝sin²y，则代入u＝sinx＋φ（sinx＋cosy）中，得sin²y＝φ（cosy）＝1－cos²y，即φ（v）＝1－v²。则φ′（v）＝－2v。故有∂u/∂y＝φ′（sinx＋cosy）（－siny）＝（－2sinx－2cosy）（－siny）＝2（sinxsiny＋cosysiny）。
第11题：

单选题
设u＝sinx＋φ（sinx＋cosy）（φ为可微函数），且当x＝0时，u＝sin2y，则∂u/∂y＝（　　）。
A
2（sinxsiny＋cosysiny）
B
2（sinxsiny－cosysiny）
C
sinxsiny＋cosysiny
D
sinxsiny－cosysiny

正确答案： C
解析：
由于x＝0，u＝sin²y，则代入u＝sinx＋φ（sinx＋cosy）中，得sin²y＝φ（cosy）＝1－cos²y，即φ（v）＝1－v²。则φ′（v）＝－2v。故有∂u/∂y＝φ′（sinx＋cosy）（－siny）＝（－2sinx－2cosy）（－siny）＝2（sinxsiny＋cosysiny）。
第12题：

单选题
设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
A
0
B
1
C
2
D
e

正确答案： B
解析：
ln（x²＋y）＝x³y＋sinx两边同时对x求导，得（2x＋y′）/（x²＋y）＝3x²y＋x³y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。
第13题：

设函数y=x3+sinx+3，求y'．

答案：
解析：
y'=(x3)'+(sinx)'+(3)'=3x2+cosx．
第14题：

设函数y=x4sinx，求dy．

答案：
解析：
因为y'=4x3sinx+x4cosx，所以dy=(4x3sinx+x4cosx)dx．
第15题：

设函数y=sin(2x+1)，则y"=_____．

答案：
解析：
填-4sin(2x+1)．
第16题：

下列各选项中，正确的是（　　）

A.y=x+sinx是偶函数
B.y=x+sinx是奇函数
C.y=｜x ｜+sinx是偶函数
D.y=｜ x ｜+sinx是奇函数

答案：B
解析：
第17题：

若函数y=(x)在[-1，1]上是单调函数，则使得y=(sinx)必为单调函数的区间是（）

A.R
B.[-1，1]
C.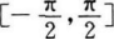
D.[-sin1，sin1]

答案：C
解析：
【考情点拨】本题主要考查的知识点为函数的单调区间． 1应试指导】y=(x)在[-1，1]上是单调函数，∴y=(x)的单调区间为[-1，1]，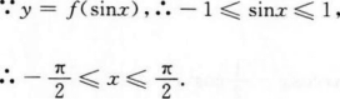
第18题：

设Y=sinx+COSx，则dy等于()．

A.(cosx+sinx)dx
B.(-cosx+sinx)dx
C.(cosx-sinx)dx
D.(-cosx-sinx)dx

答案：C
解析：
由微分的基本公式及四则运算法则可得因此选C．
第19题：

设函数y=2x+sinx，则y′=（）

A.1-cos x
B.1+cos x
C.2-cos x
D.2+cos x

答案：D
解析：
第20题：

单选题
设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
A
1
B
2
C
3
D
4

正确答案： B
解析：
ln（x²＋y）＝x³y＋sinx两边同时对x求导，得（2x＋y′）/（x²＋y）＝3x²y＋x³y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。
第21题：

单选题
若∂2u/∂x∂y＝1，且当x＝0时，u＝siny，当y＝0时，u＝sinx，则u（x，y）＝（　　）。
A
xy＋sinx－siny
B
xy＋sinx＋siny
C
x/y＋sinx－cosy
D
x/y＋sinx＋cosy

正确答案： C
解析：
u是x、y的二元函数，则∂²u/∂x∂y对y积分后应加一个关于x的函数，而不是常数C，即对∂²u/∂x∂y＝1两边对y积分得∂u/∂x＝y＋φ′（x），再两边对x积分得u（x，y）＝xy＋φ（x）＋ψ（y）。又x＝0时，u＝siny，得siny＝φ（0）＋ψ（y），即ψ（y）＝siny－φ（0）；又y＝0时，u＝sinx得sinx＝φ（x）＋ψ（0），令x＝0得φ（0）＋ψ（0）＝0。故u（x，y）＝xy＋sinx＋siny－φ（0）－ψ（0）＝xy＋sinx＋siny。
第22题：

单选题
设u＝sinx＋φ（sinx＋cosy）（φ为可微函数），且当x＝0时，u＝sin2y，则∂u/∂y＝（　　）。
A
sinxsiny＋cosysiny
B
sinxsiny＋cosycosy
C
2（sinxsiny＋cosysiny）
D
2（sinxsiny＋cosycosy）

正确答案： B
解析：
由于x＝0，u＝sin²y，则代入u＝sinx＋φ（sinx＋cosy）中，得sin²y＝φ（cosy）＝1－cos²y，即φ（v）＝1－v²。则φ′（v）＝－2v。故有∂u/∂y＝φ′（sinx＋cosy）（－siny）＝（－2sinx－2cosy）（－siny）＝2（sinxsiny＋cosysiny）。
第23题：

单选题
设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝（　　）。
A
ln1
B
0
C
sin1
D
1

正确答案： A
解析：
ln（x²＋y）＝x³y＋sinx两边同时对x求导，得（2x＋y′）/（x²＋y）＝3x²y＋x³y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

设函数y=sinx，则y"=_____．

题目

相似考题

更多“设函数y=sinx，则y"=_____．”相关问题

相关内容