袋中有8个乒乓球，其中5个白色球，3个黄色球，一次从中任取2个乒乓球， 则取出的2个球均为白色球的概率为()．A.5/8 B.5/14 C.5/36 D.5/56

题目
袋中有8个乒乓球，其中5个白色球，3个黄色球，一次从中任取2个乒乓球，
则取出的2个球均为白色球的概率为()．

A.5/8
B.5/14
C.5/36
D.5/56
相似考题

1.袋中有8个玻璃球，其中兰、绿颜色球各4个，现将其任意分成2堆，每堆4个球，则各堆中兰、绿两种球的个数相等的概率为______．

2.标有不同编号的红色球和白色球各四个,任取红色球和白色球各一个,共有________种不同的取法。A．12B．14C．16D．18

3.一个布袋里有大小相同而颜色不同的木球，其中红球10个，白球9个，蓝球2个，黄球8个。一次至少取多少个球，才能保证其中4个是同色球?()A.4B.10C.13D.12

4.：一只木箱内有白色乒乓球和黄色乒乓球若干个。小明一次取出5个黄球、3个白球，这样操作N次后，白球拿完了，黄球还剩8个；如果换一种取法：每次取出7个黄球、3个白球，这样操作M次后，黄球拿完了，白球还剩24个。问原木箱内共有乒乓球多少个？（ ）A．246个B．258个C．264个D．272个

更多“袋中有8个乒乓球，其中5个白色球，3个黄色球，一次从中任取2个乒乓球， ”相关问题

  • 第1题：

    同上题,任取两个红色球和一个白色球,共有________种不同的取法。

    A．10

    B．15

    C．20

    D．24


    正确答案：D
    解析：第一步选红色球,有(4×3)/(2×1)=6种取法;第二步选白色球,也有4种取法。根据分步计数原理,可构造6×4=24个不同的取法。

  • 第2题：

    一袋中有5个乒乓球，其中4个白球，1个红球，从中任取2个球的不可能事件是（）

    A.｛2个球都是白球｝
    B.｛2个球都是红球｝
    C.｛2个球中至少有1个白球｝
    D.｛2个球中至少有1个红球｝

    答案：B
    解析：
    袋中只有1个红球，从中任取2个球都是红球是不可能发生的．

  • 第3题：

    一位乒乓球学员手中拿着装有7只乒乓球的不透明口袋,其中3只黄球，4只白球。他随机取出一只乒乓球，观察颜色后放回袋中，同时放入2只与取出的球同色的球，这样连续取2次，则他取出的两只球中第1次取出的是白球，第2次取出的是黄球的概率是

    A.8/77
    B.4/21
    C.2/11
    D.4/7

    答案：B
    解析：
    第一步，第一次取出白球的概率为4/7。第二步，由题意取出白球后会再放入2个白球，球的总数为9。第二次取出黄球的概率为3/9=1/3，故第一次取出白球，第二次取出黄球的概率为4/7×1/3=4/21。因此，选择B选项。

  • 第4题：

    设袋中有5个球,其中3个新球,2个旧球,从中任取3个球,用X表示3个球中的新球个数,求X的分布律与分布函数.


    答案：
    解析：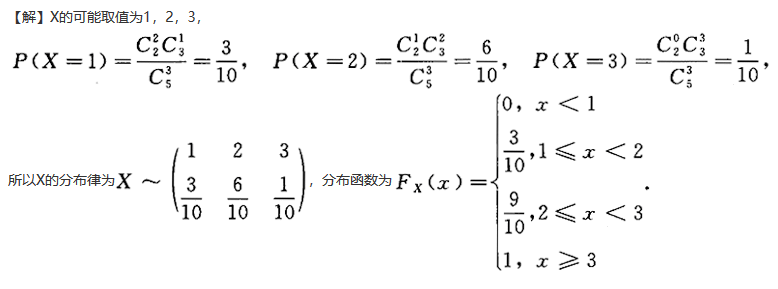

  • 第5题：

    袋中有8个乒乓球，其中5个白色球，3个黄色球，从中一次任取2个乒乓球，则取出的2个球均为白色球的概率为《》（ ）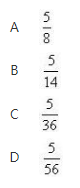


    答案：B
    解析：

  • 第6题：

    袋中有l个红色球，2个黑色球与三个白球，现有放回地从袋中取两次，每次取一球，以 X，Y，Z分别表示丽次取球所取得的红球、黑球与白球的个数。
    (1)求P{X=1|Z=0}；
    (2)求二维随机变量(X，Y)的概率分布。


    答案：
    解析：

  • 第7题：

    单击“进入资源管理器”按钮，打开N盘“球.psd”文件，该文件中有三个色球，把绿色球移动到最前面的正确操作是（）

    • A、删除红、黄色球所在的图层
    • B、把红色球及黄色球所在的图层移动到背景层下面
    • C、分别把红色球和黄色球所在的图层移动到绿色球图层的下面
    • D、无法调整

    正确答案:C

  • 第8题：

    乒乓球比赛最新规则的出现，白色小球变成了桔黄色，墨绿色球台变成了蓝色，主要是为了使运动员不易疲劳吗？


    正确答案:错误

  • 第9题：

    单击“进入资源管理器”按钮，打开N盘“球.psd”文件，该文件中有三个色球，把黄色球移动到红球和绿球后面的正确操作是（）

    • A、删除红、绿色球所在的图层
    • B、把黄色球所在的图层移动到背景层下面
    • C、分别把红色球和绿色球所在的图层移动到黄色球图层的上面
    • D、无法调整

    正确答案:C

  • 第10题：

    单选题
    在正规的乒乓球赛事中一般使用白色球和（）
    A

    黄色球

    B

    蓝色球

    C

    橙色球

    D

    紫色球


    正确答案： B
    解析： 暂无解析

  • 第11题：

    填空题
    一袋中有50个乒乓球，其中20个红球，30个白球，今两人从袋中各取一球，取后不放回，则第二个人取到红球的概率为____。

    正确答案： 2/5
    解析：
    设A：“第一个人取红球”，B：“第二个人取红球”，则
    P（B）＝P[B（A∪A(＿)）]＝P（AB）＋P（A(＿)B）＝P（B|A）P（A）＋P（B|A(＿)）P（A(＿)）＝（19/49）×（20/50）＋（20/49）×（30/50）＝2/5

  • 第12题：

    单选题
    一只木箱内有白色乒乓球和黄色乒乓球若干个。小明一次取出5个黄球，3个白球，这样操作N次后，白球拿完了，黄球还剩8个；如果换一种取法：每次取出7个黄球，3个白球，这样操作M次后，黄球拿完了，白球还剩24个。问原木箱内共有乒乓球多少个？（　　）
    A

    246个

    B

    258个

    C

    264个

    D

    272个


    正确答案： D
    解析：
    两种取法，白球的总数和黄球的总数相等，则5N＋8＝7M，3N＝3M＋24，得N＝32，M＝24，则木箱内共有乒乓球（5＋3）×32＋8＝264个。

  • 第13题：

    袋中有5个白球和3个黑球，从中任取两球，则取得的两球颜色相同的概率为13/28。()


    正确答案:对

  • 第14题：

    袋中装有大小相同的12个球，其中5个白球和7个黑球，从中任取3个球，求
    这3个球中至少有1个黑球的概率．


    答案：
    解析：
    此题利用对立事件的概率计算较为简捷，

  • 第15题：

    标有不同编号的红色球和白色球各四个，任取两个红色球和一个白色球，共有（ ）种不同的取法。A. 10 B. 15 C. 20 D. 24


    答案：D
    解析：
    第一步选红色球，有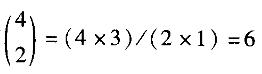种取法；第二步选白色球，有4种取法。根据乘法原理，共有：6x4 =24种不同的取法。

  • 第16题：

    袋中有50个乒乓球，其中20个是黄球，30个是白球，今有两人依次随机地从袋中各取一球，取后不放回，则第二个人取得黄球的概率是________.


    答案：
    解析：
    一般理解随机事件“第二个人取得黄球”与第一个人取得的是什么球有关，这就要用全概率公式来计算，但也可以用古典型概率来解，这会简单得多.(方法一)设事件Ai表示第i个人取得黄球，i=1，2，则根据全概率公式：

    (方法二)只考虑第二个人取得的球，这50个球中每一个都会等可能地被第二个人取到，而取到黄球的可能有20个，故所求概率为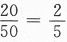

  • 第17题：

    袋中有50个乒乓球，其中20个黄的，30个白的，现在两个人不放回地依次从袋中随机各取一球。则第二人取到黄球的概率是（ ）

    A.1/5
    B.2/5
    C.3/5
    D.4/5

    答案：B
    解析：

  • 第18题：

    福利彩票双色球“6+1”选号范围是（）

    • A、33个蓝色球和16红色球
    • B、33个红色球和16蓝色球

    正确答案:B

  • 第19题：

    袋中有4个白球2个黑球，今从中任取3个球，则至少一个黑球的概率为（）

    • A、4/5
    • B、1
    • C、1/5
    • D、1/3

    正确答案:A

  • 第20题：

    在正规的乒乓球赛事中一般使用白色球和（）

    • A、黄色球
    • B、蓝色球
    • C、橙色球
    • D、紫色球

    正确答案:C

  • 第21题：

    判断题
    乒乓球比赛最新规则的出现，白色小球变成了桔黄色，墨绿色球台变成了蓝色，主要是为了使运动员不易疲劳吗？
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第22题：

    单选题
    福利彩票双色球“6+1”选号范围是（）
    A

    33个蓝色球和16红色球

    B

    33个红色球和16蓝色球


    正确答案： A
    解析： 暂无解析

  • 第23题：

    单选题
    袋中有5个白球 ，n个红球，从中任取一个恰为红球的概率为2/3，则n为(　　)
    A

    16  

    B

    10  

    C

    20   

    D

    18


    正确答案： B
    解析： 根据概率的定义：P=n/5+n=2/3

相关内容