设三个事件A、B、C相互独立，某发生概率相等，都为2/3，则A、B、C中至少发生一个的概率为（ ）。A.8/27B.1/27C.19/27D.26/27

题目

设三个事件A、B、C相互独立，某发生概率相等，都为2/3，则A、B、C中至少发生一个的概率为（ ）。

A.8/27

B.1/27

C.19/27

D.26/27

相似考题

1.设随机事件A在某试验中发生的概率为0.6,进行三次独立的试验,求至少有两次事件A发生的概率。

2.设事件A发生的概率为0．7，则A的对立事件A发生的概率为.

3.事件A，B相互独立，A，B发生的概率分别为0．6，0．9，则A，B都不发生的概率为()．A.0．54 B.0．04 C.0．1 D.0．4

4.设随机事件A、B相互独立，其发生概率均为2/3，则A，B中至少有一个发生的概率为（ ）。A.1B.8/9C.4/9D.1/9

参考答案和解析
正确答案：D
D。
更多“设三个事件A、B、C相互独立，某发生概率相等，都为2/3，则A、B、C中至少发生一个的概率为（ ）。A.8/27B.1/27C.19/27D.26/27”相关问题

  • 第1题：

    设三个事件A、B、C相互独立，发生概率均为1/3，则A、B、C中恰好发生一个的概率为（ ）。
    A. 1/9 B. 2/9 C. 4/9 D. 5/9


    答案：C
    解析：
    依题意，A、B、C三个事件中恰好发生一个的概率为：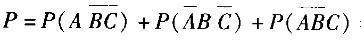
    =1/3 x2/3 x2/3 +1/3 x2/3 +2/3 x2/3 x1=4/9。

  • 第2题：

    设一次试验中,出现事件A的概率为P,则n次试验中A至少发生一次的概率为_______,A至多发生一次的概率为_______.


    答案：
    解析：

  • 第3题：

    设两个相互独立的事件A和B都不发生的概率为，A发生，B不发生的概率与B发生A不发生的概率相等，则P(A)=________.


    答案：
    解析：
    由题设条件P(A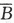)=P(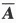B)推出P(A)=P(B)，再加上A,B独立，解得P(A)=.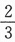

  • 第4题：

    设三个事件A、B、C相互独立，其发生概率相等，都为2/3，则A、B、C中至少发生一个的概率为（ ）。[2008年真题]
    A. 8/27 B. 1/27 C. 19/27 D. 26/27


    答案：D
    解析：
    根据题意，A、B、C三个事件不发生的概率均为：1－2/3 =1/3。而A、B、C中至 少发生一个的对立事件是三者都不发生，由于三个事件独立，所以三者均不发生的概率为: 1/3×1/3×1/3=1/27，那么A、B、C中至少发生一个的概率为：1－1/27 = 26/27。

  • 第5题：

    设三个事件A、B、C相互独立，某发生概率相等，都为2/3，则A、B、C中至少发生一个的概率为（ ）。
    A. 8/27 B. 1/27
    C. 19/27 D. 26/27


    答案：D
    解析：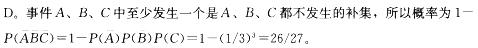

  • 第6题：

    设三台机器相互独立运转，第一、第二、第三台机器不发生故障的概率依次为0.9，0.8和0.7，则这三台机器中至少有一台发生故障的概率为（）。


    正确答案:0.496

  • 第7题：

    单选题
    随机事件A和B相互独立，且P（A）＝1/2，P（B）＝1/3，则A和B中仅有一个发生的概率为（　　）。
    A

    5/6

    B

    2/3

    C

    1/2

    D

    1/3


    正确答案： B
    解析：
    因为A(＿)B，AB(＿)互不相容，故P（A(＿)B∪AB(＿)）＝P（A(＿)B）＋P（AB(＿)），又A，B相互独立，故上式可化简为：上式＝P（A）P（B(＿)）＋P（A(＿)）P（B）＝P（A）[1－P（B）]＋[1－P（A）]P（B）＝（1/2）×（2/3）＋（1/3）×（1/2）＝1/2。

  • 第8题：

    问答题
    25.设A与B相互独立，两个事件仅A发生和仅B发生的概率都是

    正确答案：
    解析：

  • 第9题：

    单选题
    某居民小区有两个相互独立的安全防范系统A和B，系统A和系统B在任意时刻发生故障的概率分别为1/10和p，若在任意时刻至少有一个系统不发生故障的概率为49/50，则系统B在3次相互独立的检测中不发生故障的次数大于发生故障的次数的概率：
    A

    小于85%

    B

    在85%—90%之间

    C

    在90%—95%之间

    D

    大于95%


    正确答案： B
    解析： 暂无解析

  • 第10题：

    填空题
    设一次试验中事件A发生的概率为p，又若已知三次独立试验中A至少出现一次的概率等于37/64，则p＝____。

    正确答案： 1/4
    解析：
    因1－C30p0（1－p）3＝37/64，故p＝1/4。

  • 第11题：

    填空题
    设两个相互独立的事件A和B都不发生的概率为1/9，A发生B不发生的概率与B发生A不发生的概率相等，则P（A）＝____。

    正确答案： 2/3
    解析：
    因为A，B独立，且P（A(＿)B）＝P（AB(＿)），所以P（A(＿)）P（B）＝P（A）P（B(＿)），即P（B）－P（A）P（B）＝P（A）－P（A）P（B），推得P（A）＝P（B）。又P（A(＿)B(＿)）＝[P（A(＿)）]2＝[1－P（A）]2＝1/9，故P（A）＝2/3。

  • 第12题：

    填空题
    设事件A和B中至少有一个发生的概率为5/6，A和B中有且仅有一个发生的概率为2/3，那么A和B同时发生的概率为____。

    正确答案： 1/6
    解析：
    根据题意P（A(＿)B）＋P（AB(＿)）＝2/3，P（A∪B）＝5/6，故P（AB）＝P（A∪B）－[P（A(＿)B）＋P（AB(＿)）]＝5/6－2/3＝1/6。

  • 第13题：

    设三个事件A、B、C相互独立，某发生概率相等，都为2/3，则A、B、C中至少发生一个的概率为（ ）。
    A. 8/27 B. 1/27
    C.19/27 D. 26/27


    答案：D
    解析：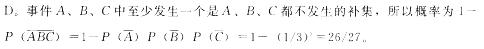

  • 第14题：

    设A,B相互独立,只有A发生和只有B发生的概率都是,则P(A)=_______.


    答案：
    解析：

  • 第15题：

    三次独立试验中A发生的概率不变,若A至少发生一次的概率为,则一次试验中A发生的概率为_______.


    答案：
    解析：
    设一次试验中A发生的概率为p，B={三次试验中A至少发生一次}，则P(B)=

  • 第16题：

    设随机事件A、B相互独立，其发生概率均为2/3，则A, B中至少有一个发生的概率为（ ）。
    A. 1 B. 8/9
    C. 4/9 D. 1/9


    答案：B
    解析：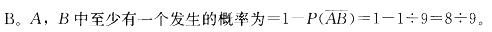

  • 第17题：

    如果事件1发生的概率是80％，事件2发生的概率是70％，这们又是相互独立的事件，那么这两个事件都发生的概率是多大？（）

    • A、6％
    • B、15％
    • C、24％
    • D、56％

    正确答案:D

  • 第18题：

    如果事件1发生的概率为80%，事件2为70%，而且两个事件均是独立事件，则它们都发生的概率是：（）。

    • A、6%
    • B、15%
    • C、24%
    • D、56%

    正确答案:D

  • 第19题：

    单选题
    设三个事件A、B、C相互独立，其发生概率相等，都为2/3，则A、B、C中至少发生一个的概率为（　　）。[2008年真题]
    A

    8/27

    B

    1/27

    C

    19/27

    D

    26/27


    正确答案： C
    解析： 根据题意，A、B、C三个事件不发生的概率均为:1-2/3=1/3。而A、B、C中至少发生一个的对立事件是三者都不发生，由于三个事件独立，所以三者均不发生的概率为:1/3×1/3×1/3=1/27，那么A、B、C中至少发生一个的概率为:1-1/27＝26/27。

  • 第20题：

    单选题
    设事件A和B中至少有一个发生的概率为5/6，A和B中有且仅有一个发生的概率为2/3，那么A和B同时发生的概率为（　　）。
    A

    1/6

    B

    5/6

    C

    2/3

    D

    1/2


    正确答案： D
    解析：
    根据题意P（A(＿)B）＋P（AB(＿)）＝2/3，P（A∪B）＝5/6，故P（AB）＝P（A∪B）－[P（A(＿)B）＋P（AB(＿)）]＝5/6－2/3＝1/6。

  • 第21题：

    问答题
    13.设A，B，C为三个随机事件， P(AC)=0．求 (1)A，B，C中至少有一个发生的概率; (2)A，B，C全不发生的概率．

    正确答案：
    解析： 暂无解析

  • 第22题：

    单选题
    某居民小区有两个相互独立的安全防范系统A和B，系统A和系统B在任意时刻发生故障的概率分别为击和p，若在任意时刻至少有一个系统不发生故障的概率为49，则系统B在3次相互独立的检测中不发生故障的次数大于发生故障的次数的概率：
    A

    小于85%

    B

    在850%～90%之间

    C

    在90%—95%之间

    D

    大于95%


    正确答案： C
    解析： 暂无解析

  • 第23题：

    单选题
    设两个相互独立的事件A和B都不发生的概率为1/9，A发生B不发生的概率与B发生A不发生的概率相等，则P（A）＝（　　）。
    A

    1/9

    B

    2/3

    C

    1/3

    D

    1/6


    正确答案： A
    解析：
    因为A，B独立，且P（A(＿)B）＝P（AB(＿)），所以P（A(＿)）P（B）＝P（A）P（B(＿)），即P（B）－P（A）P（B）＝P（A）－P（A）P（B），推得P（A）＝P（B）。又P（A(＿)B(＿)）＝[P（A(＿)）]2＝[1－P（A）]2＝1/9，故P（A）＝2/3。

相关内容