对方程作显著性检验时,下列叙述( )是正确的。A.残差平方和的自由度为25B.残差平方和的自由度为24C.检验统计量F的值为24.986D.检验统计量,的值为43.074
题目
对方程作显著性检验时,下列叙述( )是正确的。
A.残差平方和的自由度为25
B.残差平方和的自由度为24
C.检验统计量F的值为24.986
D.检验统计量,的值为43.074
相似考题
参考答案和解析
正确答案:BC
更多“对方程作显著性检验时,下列叙述( )是正确的。A.残差平方和的自由度为25B.残差平方和的 ”相关问题
-
第1题:
在对方程的总(离差)平方和作分解时,下列计算正确的是( )。
A.回归平方和是33.504
B.残差平方和为24.123
C.回归平方和是41.563
D.残差平方和为32.182
正确答案:AD
-
第2题:
某厂生产白水泥,对每一窑生产的水泥都需要测定其抗压强度,以确定水泥标号,一般是将水泥出窑后做成的试块养护28天所测得的数据为准。但是水泥不可能堆放28天后再出厂,所以考虑用7天的抗压强度x来预测28天的抗压强度y。现在统计了26窑的数据,求得的结果为: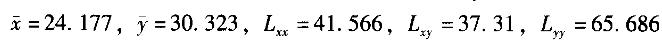 ,假定在显著性水平a =0.05上查表得到相关系数的临界值为0.388,F分布的临界值为4. 26。
,假定在显著性水平a =0.05上查表得到相关系数的临界值为0.388,F分布的临界值为4. 26。
对方程作显著性检验时,下列叙述正确的是( )。
A.残差平方和的自由度为24 B.残差平方和的自由度为25
C.检验统计量F的值为24. 986 D.检验统计量F的值为43. 074答案:A,C解析:根据题意得,n=26,所以总离差平方和的自由度为fT = n-1=25,回归平方和的自由度为fR =1,从而残差平方和的自由度为fE =fT-fR =24,检验统计量F的值为:
-
第3题:
根据两个变量的18对观测数据建立一元线性回归方程。在对回归方程作检验时,残差平方和的自由度为
A.16
B.17
C.18
D.1
C 残差平方和的自由度fE=n-2=观测值个数-2=18-2=16。 -
第4题:
根据两个变量的18对观测数据建立一元线性回归方程。在对回归方程作检验时,残差平方和的自由度为( )。
A. 18 B. 17
C. 16 D. 1答案:C解析:。残差平方和的自由度fE=n—2=观测值个数一2 = 18 —2 = 16。 -
第5题:
根据18对观测值(xi,yi),i=1,2,…,18,建立了一光线性回归方程。在对该回归方程作显著性检验时,其回归平方和的自由度fR与残差平方和的自由度fE分别为( )
A.fR=1
B.fR= 2
C.fE=18
D.fE=17
E.fE=16答案:A,E解析:。fE=n-2=18-2=16
