同上题,任取两个红色球和一个白色球,共有________种不同的取法。A.10B.15C.20D.24
题目
同上题,任取两个红色球和一个白色球,共有________种不同的取法。
A.10
B.15
C.20
D.24
相似考题
参考答案和解析
正确答案:D
解析:第一步选红色球,有(4×3)/(2×1)=6种取法;第二步选白色球,也有4种取法。根据分步计数原理,可构造6×4=24个不同的取法。
解析:第一步选红色球,有(4×3)/(2×1)=6种取法;第二步选白色球,也有4种取法。根据分步计数原理,可构造6×4=24个不同的取法。
更多“同上题,任取两个红色球和一个白色球,共有________种不同的取法。A.10B.15C.20D.24 ”相关问题
-
第1题:
标有不同编号的红色球和白色球各四个,任取两个红色球和一个白色球,共有( )种不同的取法。A. 10 B. 15 C. 20 D. 24答案:D解析:第一步选红色球,有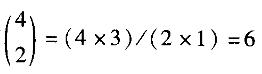 种取法;第二步选白色球,有4种取法。根据乘法原理,共有:6x4 =24种不同的取法。
种取法;第二步选白色球,有4种取法。根据乘法原理,共有:6x4 =24种不同的取法。 -
第2题:
三个袋子里分别装有9个红色球,8个蓝色球和10个白色球.任取出一个球,共有27种取法。
27;27种 -
第3题:
三色球问题。若一个口袋中放有12个球,其中有3个红色的,3个白色的,6个黑色的,从中任取8个球,问共有多少种不同的颜色搭配?这个问题可以采用穷举法求解,设任取的红、白、黑球个数分别为i,j,k。依题意,红、白、黑球个数的穷举范围分别为0<=i<=3,0<=j<=3,0<=k<=6。只要满足(),则i,j,k的组合即为所求。
A.i+j+k=8
B.i+j+k=12
C.i=3并且j=3并且k=6
D.i=3或者j=3或者k=6
B -
第4题:
袋中有8个乒乓球,其中5个白色球,3个黄色球,从中一次任取2个乒乓球,则取出的2个球均为白色球的概率为《》( )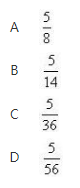 答案:B解析:
答案:B解析: -
第5题:
箱子中有5个红球,4个白球,至少要取()个才能保证有3个同色球。
3/11
