一种电子元件的正常寿命服从λ=0.1的指数分布，则这个电子元件可用时间在100小时之内的概率为（ ）。 A. 99. 05% B. 99. 85% C. 99. 95% D. 99. 99%
题目
A. 99. 05% B. 99. 85% C. 99. 95% D. 99. 99%
相似考题
更多“一种电子元件的正常寿命服从λ=0.1的指数分布，则这个电子元件可用时间在100小时之内的概率为（ ）。 ”相关问题
-
第1题：
某产品的寿命(单位：小时)服从参数λ=0.005的指数分布，则下列说法正确的有( )。
A．产品的平均寿命为200小时
B．产品的平均寿命为500小时
C．失效率为0.005
D．1000小时的可靠度为e-5
E．产品寿命超过2000小时的概率为e-5
正确答案：ACD
解析：当产品的寿命服从指数分布时，产品的平均寿命，故某产品的平均寿命；失效率为常数，λ=0.005；可靠度R(t)=e-λt=e-0.005t，因此及(1000)=e-0.005×1000=e-5，产品寿命超过2000小时的概率为：R(2000)=e-0.005×2000=e-10。 -
第2题：
已知X服从指数分布Exp(λ)，其概率密度函数为：p(x)=λe-λx，x≥0，在λ=0.1的情况下，P(5≤X≤20)=( )。
A．0.1353
B．0.4712
C．0.6065
D．0.7418
正确答案：B
解析：P(5≤X≤20)=。 -
第3题：
对某天生产的2000件电子元件的耐用时间进行全面检测，又抽取5%进行抽样复测，资料如表5-1所示。
规定耐用时间在3000小时以下为不合格品，则该电子元件合格率的抽样平均误差为 ( )。
A．1.63%
B．1.54%
C．1.52%
D．1.35%
正确答案：C
解析：由题意知，规定耐用在3000小时以下为不合格产品，则全部元件的合格率为P=。抽取5%进行复测，共抽取的样本容量n=2000×5%=100，N=2000，不重复抽样条件下：。 -
第4题：
为了考察某种类型的电子元件的使用寿命情况，假定该电子元件使用寿命的分布是正态分布。而且根据历史记录得知该分布的参数为：平均使用寿命μ0为100小时，标准差a为10小时。现在随机抽取100个该类型的电子元件，测得平均寿命为102小时，给定显著性水平a=0．05，为了判断该电子元件的使用寿命是否有明显的提高，下列说法正确的有（ ）。
答案：A,C,D,E解析：
-
第5题：
某产品的寿命服从指数分布，若失效率为0.002，则该产品的平均寿命为（）
- A、200
- B、1000
- C、500
- D、2000
正确答案:C -
第6题：
某电子产品的寿命服从指数分布，故障率为0.1/h，则工作4小时不发生故障的概率是（）。
- A、0.33
- B、0.4
- C、0.1
- D、0.67
正确答案:D -
第7题：
设产品寿命服从指数分布，在t=MTBF时刻，产品的可靠度为（）。
- A、e1.1
- B、e-0.1
- C、e-l
- D、e-0.001
正确答案:C -
第8题：
寿命服从指数分布的产品，当工作时间等于产品的平均寿命时，有一半的产品能正常工作
正确答案:错误 -
第9题：
单选题若产品的寿命服从指数分布，则故障率的倒数是( )。A平均维修时间
B平均故障间隔时间
C失效概率
D系统可靠性
正确答案： C解析： 暂无解析 -
第10题：
问答题40.已知某种类型电子元件的寿命X(单位：小时)服从指数分布，它的概率密度为 一台仪器装有4个此种类型的电子元件，其中任意一个损坏时仪器便不能正常工作．假设4个电子元件损坏与否互相独立． 试求：(1)一个此种类型电子元件能工作2 000小时以上的概率p1； (2)一台仪器能正常工作2 000小时以上的概率p2．正确答案：解析： -
第11题：
填空题某产品寿命服从参数λ为0.001的指数分布，则其平均寿命为：（）。正确答案： 1000解析： 暂无解析 -
第12题：
填空题有一寿命服从指数分布的产品，当工作时间等于产品的平均寿命时，产品能正常工作的可能性为（），当工作时间等于产品平均寿命的1/10时，产品的可靠度是（）。正确答案： 36.79%，90.48%解析： 暂无解析 -
第13题：
已知X服从指数分布Exp(0.1),则P(5≤X≤20)=________。
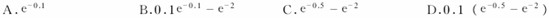
A．
B．
C．
D．
正确答案：C
-
第14题：
为了考察某种类型的电子元件的使用寿命情况，假定该电子元件使用寿命的分布是正态分布。而且根据历史记录得知该分布的参数为：平均使用寿命μ0为100小时，标准差口为10小时。现在随机抽取100个该类型的电子元件，测得平均寿命为102小时，给定显著性水平α=0.05，为了判断该电子元件的使用寿命是否有明显的提高，下列说法正确的有( )。
A．提出假设H0:μ≤100；H1:μ＞100
B．提出假设H0:μ≥100；H1:μ＜100
C．检验统计量及所服从的概率分布为
D．如果Z＞Zα，则称
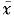与μ0的差异是显著的，这时拒绝H0E．检验结果认为该类型的电子元件的使用寿命确实有显著提高
正确答案：ACDE
解析：这是σ2已知的，关于总体均值μ的右侧检验，所以假设检验步骤如下：①提出假设H0):μ≤100；H1:μ＞100；②计算统计量：③求出拒绝域：因为Za=Z0.05=1.645，所以拒绝域为：[1.645，+∞)；④做出统计判断：因为Z＞Za=1.645，所以拒绝H0，接受H1，即当显著性水平等于0.05时，可认为该类型的电子元件的使用寿命确实有显著提高。 -
第15题：
装配某仪器要用到228个元器件，使用更先进的电子元件后，只要22个就够了。如果每个元器件或电子元件能正常工作1000小时以上的概率为0. 998，并且这些元件工作状态是相互独立的，仪表中每个元件都正常工作时，仪表才能正常工作，则两种场合下仪表能正常工作1000小时的概率分别为（ ）。
A. 0.595; 0.952 B. 0.634; 0.957
C. 0. 692; 0. 848 D. 0.599; 0.952答案：B解析：设事件A = “仪表正常工作1000小时”，事件Ai=“第i个元件能正常工作1000 小时”，则：①用元器件时有：P(A) =P(A1)P(A2)…P(A228) =0.998228 =0.634；②用电子元件时有：P(A)=P(A1)P(A2)P(A3)…P(A22)=0.99822 =0.957。 -
第16题：
设总体X服从指数分布，概率密度为（ ）。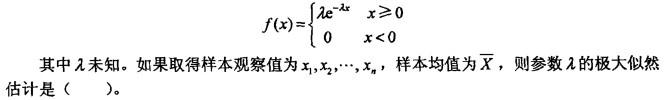
答案：D解析：
-
第17题：
有一寿命服从指数分布的产品，当工作时间等于产品的平均寿命时，产品能正常工作的可能性为（），当工作时间等于产品平均寿命的1/10时，产品的可靠度是（）。
正确答案:36.79%，90.48% -
第18题：
某产品的寿命为指数分布，故障率为0.1/小时，则工作3小时不发生故障的概率是（）。
- A、0.2592
- B、0.3
- C、0.7408
- D、0.1
正确答案:C -
第19题：
电子元件厂日产10000只元件，经多次一般测试得知一等品率为92%，现拟采用随机抽样方式进行抽检，如果求误差范围在2%之内，可靠程度为95.45%，需抽取（）电子元件。
正确答案:686 -
第20题：
判断题寿命服从指数分布的产品，当工作时间等于产品的平均寿命时，有一半的产品能正常工作A对
B错
正确答案： 对解析： 暂无解析 -
第21题：
问答题某工厂收到供货方发来的一批电子元件的例子中，共抽取了10件电子元件进行检验，使用样本的方差为S2=8000.56（小时）。试在95％的置信概率下对该批电子元件使用寿命的方差和标准差进行区别。正确答案：解析： -
第22题：
单选题若产品的寿命服从指数分布，则故障率的倒数是（ ）。[2006年真题]A平均维修时间
B平均故障间隔时间
C失效概率
D系统可靠性
正确答案： A解析：
当产品的寿命服从指数分布时，产品的故障率为常数λ，则平均故障间隔时间MTBF＝MTTF＝1/λ。 -
第23题：
单选题某产品的寿命服从指数分布，若失效率为0.002，则该产品的平均寿命为（）A200
B1000
C500
D2000
正确答案： B解析： 暂无解析