假设市场上存在一种无风险债券，债券收益率为6%，同时存在一种股票，期间无 分红，目前的市场价格是100元，该股票的预期收益率为20%(年率）。如果现在存在该股 票的1年期远期合约,远期价格为107元，那么理论上说投资者会（ ）。 A.买进远期合约的同时卖出股票 B.卖出远期合约和债券的同时买进股票 C.卖出远斯合约的同时买进股票 D.买进远期合约和债券的同时卖出股票
题目
A.买进远期合约的同时卖出股票 B.卖出远期合约和债券的同时买进股票
C.卖出远斯合约的同时买进股票 D.买进远期合约和债券的同时卖出股票
相似考题
更多“假设市场上存在一种无风险债券，债券收益率为6%，同时存在一种股票，期间无 分红，目前的市场价格是100元，该股票的预期收益率为20%(年率）。如果现在存在该股 票的1年期远期合约,远期价格为107元，那么理论上说投资者会（ ）。 ”相关问题
-
第1题：
某股票最近每股派发现金股利0.5元，并且预计保持每年6%的增长率。如果经过计算得到该股票的β值为1.1，并且知道目前的无风险收益率为4%，股票市场的总体收益率为9%。那么，该股票的理论价格为（ ）。
A．7.65元
B．12.04元
C．7.35元
D．15.14元
答案：D
解析：该股票预期收益率为k=4%+1.1×(9%-4%)=9.5%，
则P0=D0(1+g)/k-g=0.5×(1+6%)/(9.5%-6%)=15.14（元）。
-
第2题：
某股票的β值为1.5，无风险收益率为6%，市场收益率为14%，如果该股票的期望收益率为20%，那么该股票的价格()。A:被低估
B:被高估
C:无法判断
D:是公平价格答案：A解析：根据CAPM模型，均衡时，该股票的理论收益率为：6%+1.5*(14%-6%)=18%，而该股票的期望收益率为20%，表明该股票的价格被低估，是值得投资的。 -
第3题：
假设你正在考虑投资某股票,该股票的永续股利为6元/股,根据你的调查,该股票的β系数为0.9。当前的无风险收益率为4.3%,市场期望收益率是13%。 (1)如果选择用CAPM模型进行估计,计算你对该股票的期望收益率是多少? (2)根据期望收益率,你愿意为该股票支付多少钱? (3)假设你的调查出了错误,该股票的实际β值为1.3,则如果你以(2)中的价格购买该股票,则你是高估其价格还是低估其价格?答案：解析：
CAPM与股利贴现模型一一戈登公式的简单应用,属于非常基本的内容,由 此可见复旦的计算题难度并非强调解题的困难。 -
第4题：
票息率为5%的3年期债券，市场价格为100元，到期收益率为5%，麦考利久期为2.86年，如果该债券的到期收益率下降至4.9%，那么该债券的价格变动为（ ）。A.上涨0.495元
B.下跌0.272元
C.上涨0.272元
D.下跌0.495元答案：C解析： -
第5题：
某投资者买入一只股票 6个月的远期合约空头，已知该股票目前的价格为40元，预计在2 个月和 5个月后每股分别派发股息 1 元，一年期无风险利率为 6%。 3个月后，该股票价格涨到45元，无风险利率仍为6%，此时远期合约空头价值约为（）元。
- A、-5.35
- B、-5.4
- C、-5.5
- D、-5.6
正确答案:C -
第6题：
某投资者买入一只股票6个月的远期合约空头，已知该股票目前的价格为40元，预计在2个月和5个月后每股分别派发股息1元，一年期无风险利率为6%。若交割价格等于远期价格，则远期合约的价值是（）元。
- A、0
- B、38.19
- C、38.89
- D、39.19
正确答案:A -
第7题：
目前市场上的无风险收益率为10%，市场平均的股票收益率为14%，甲公司的股票β系数为0.6，则该股票预期的收益率为（）。
- A、10%
- B、14%
- C、12.4%
- D、12%
正确答案:C -
第8题：
单选题假设一只无红利支付的股票当前股价为20元，无风险连续复利为0.05，则该股票1年期的远期价格是（ ）元。A20
B20.05
C21.03
D10.05
正确答案： A解析： -
第9题：
单选题一种5年期债券的现货价格为950元，该债券1年期远期合约的交割价格为960元，该债券在6个月末和12个月末都将收到50元的利息，且第二次付息日在远期合约交割日之前。假设6个月期和22个月期的无风险年利率（连续复利）分别为9％和10％，则该远期合约空头的价值为（ ）元。A12.43
B11.68
C14.43
D-14.43
E-11.68
正确答案： A解析：
该债券已知现金收益的现值为：
I=50e-0.09×0.5+50e-0.10×1=93.04（元）
该远期合约多头的价值为：
f=950-93.04-960e-0.1×1=-11.68（元）
相应地，该合约空头的价值为11.68元。 -
第10题：
单选题假定投资者正考虑买入1股股票，价格为50元。该股票来年派发的红利预计为3元，投资者预期可以52元卖出。股票风险的β值为-0.5，关于该股票说法正确的是（ ）。A预期收益率为0.015，股票价格被高估
B预期收益率为0.1，股票价格被低估
C预期收益率为0.025，股票价格被高估
D预期收益率为0.015，股票价格被低估
E预期收益率为0.105，股票价格被高估
正确答案： E解析：
当股票的β值为-0.5时，其预期收益率应该为：r=0.06-0.5×（0.15-0.06）=0.015，根据题目条件，股票实际收益率应为：（3+52-50）/50=0.1＞0.015，所以，该股票的价格被低估。 -
第11题：
单选题某股票预计在2个月和5个月后分别派发股息1元/股，该股票目前价格是30元/股，所有期限的无风险连续利率均为6%，某投资者持有该股票6个月期的远期合约空头。 若交割价格等于远期价格，则远期合约的价值是（）元。A0
B28.19
C28.89
D29.19
正确答案： B解析： 暂无解析 -
第12题：
单选题某投资者买入一只股票6个月的远期合约空头，已知该股票目前的价格为40元，预计在2个月和5个月后每股分别派发股息1 元，一年期无风险利率为 6%。 该股票6个月后的远期价格等于（）元。A38.19
B38.89
C39.19
D39.89
正确答案： C解析： 暂无解析 -
第13题：
假设ABC公司股票目前的市场价格为28元，而在6个月后的价格可能是40元和20元两种情况。再假定存在一份100股该种股票的看涨期权，期限是半年，执行价格为28元。投资者可以按10%的无风险年利率借款。购进上述股票且按无风险年利率10%借入资金，同时售出一份100股该股票的看涨期权。
要求：
(1)根据单期二叉树期权定价模型，计算一份该股票的看涨期权的价值。
(2)假设股票目前的市场价格、期权执行价格和无风险年利率均保持不变，若把6个月的时间分为两期，每期3个月，若该股票收益率的标准差为0.08，计算每期股价上升百分比和股价下降百分比。
(3)结合(2)分别根据套期保值原理和风险中性原理，计算一份该股票的看涨期权的价值。
正确答案：(1)股价上升百分比＝(40－28)/28＝42.86%，股价下降百分比＝(20－28)/28＝－28.57%
期权的价值C0＝[W1×Cu+(1－w1)×Cd]÷(1+r)
＝
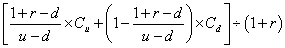
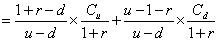
将r＝5%，u＝1.4286，d＝1－0.2857＝0.7143，Cu＝1200，Cd＝0代入上式。
期权的价值C(元)
(2)u＝1+上升百分比＝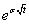
＝
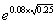＝1.0408，上升百分比＝4.08%
d＝1－下降百分比＝1/u＝1/1.0408＝0.9608，下降百分比＝3.92%
(3)①根据套期保值原理：
套期保值比率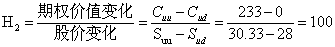
借入资金数额(元)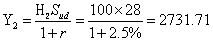
万元，属于沉没成本，即无关成本，不予考虑。另外，部分考生受到了
Cu＝购买股票支出－借款＝H2Su－Y2＝100×29.14－2731.71＝182.29(元)
Cd＝0 _
套期保值比率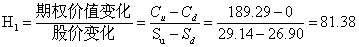
借入资金数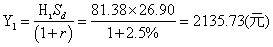
CO＝购买股票支出－借款＝H1SO－Y1＝81.38×28－2135.73＝142.91(元)
②根据风险中性原理：序号 0
1
2
28
29.14
30.33
期权价格
26.90
28
25.85
142.82(或142.91)
182.42(或182.29)
233
期权价格
0
0
0
期望报酬率＝上行概率×股价上升百分比+下行概率×股价下降百分比
＝上行概率×股价上升百分比+(1－上行概率)×股价下降百分比
即：2.5%＝上行概率×4.08%+(1－上行概率)×(－3.92%)
上行概率＝80.25%
期权价值6个月后的期望值＝80.25%×233+(1－80.25%)×0＝186.98(元)
Cu＝186.98/(1+2.5%)＝182.42(元)
期权价值3个月后的期望值＝80.25%×182.42+(1－80.25%)×0＝146.39(元)
期权的现值＝146.39/(1+2.5%)＝142.82(元)。 -
第14题：
假设S公司的股票上年度发放的股利为0.9元/股，并预期以后各年度的股利水平都一样。如果投资者对该股票要求的收益率为15%，则该股票当前的价格该为()。A:6元/股
B:8元/股
C:19元/股
D:10元/股答案：A解析： -
第15题：
某股票每年支付一次固定红利，直至永远，其市场价格为50元，年化预期收益率为14%，市场组合的年化风险溢价为5%，年化无风险利率为6%。
(1)假设CAPM模型成立，求此股票的贝塔值?
(2)该股票每年每股支付多少固定红利?
(3) 如果该股票收益率与市场组合收益率的协方差变成原来的两倍(其他条件保持不变)该股票的市场价格应为多少?答案：解析：
-
第16题：
假设一支无红利支付的股票当前股价为40元，无风险连续复利为0.05，则该股票1年期的远期价格为( )元。A.40.005
B.40.072
C.42.055
D.42.062答案：D解析：无红利股票的远期价格公式为：Ft=Ster(T－t)，将数据代入公式，Ft=40e0.05=42.062(元)。 -
第17题：
某投资者买入一只股票6个月的远期合约空头，已知该股票目前的价格为40元，预计在2个月和5个月后每股分别派发股息1 元，一年期无风险利率为 6%。 该股票6个月后的远期价格等于（）元。
- A、38.19
- B、38.89
- C、39.19
- D、39.89
正确答案:C -
第18题：
无风险资产收益率为7%，某股票A的预期收益率为15%，标准差为20%，如果由无风险资产和股票A构成的投资组合的预期收益率为13%，那么该组合的标准差为（）。
- A、15%
- B、20%
- C、0
- D、17%
正确答案:A -
第19题：
问答题某公司股票的β系数为2.5，目前无风险收益率为6%，市场上所有股票的平均报酬率为10%，若该股票为固定增长股票，增长率为6%，预计一年后的每股股利为1.5元。 要求： （1）测算该股票投资人要求的必要投资收益率。 （2）该股票的价格为多少时可购买。 （3）若股票目前的市价为14元，预期1年后的市价为15元，那么投资人持有一年后出售的内部收益率为多少？正确答案：
(1)该股票的必要投资收益率=Rf+β×(Rm-Rf)=6%+2.5×(10%-6%)=16%
(2)股票的价值=D1/(Rs-g)=1.5/(16%-6%)=15(元),则当股票价格低于15元时,可以购买。
(3)该股票未来现金流量有股票出售可得15元,一年后的股利1.5元,由净现值=0可得:(15+1.5)/(1+R)-14=0
内部收益率R=(15+1.5)/14-1=17.86%。解析： 暂无解析 -
第20题：
单选题某股票预计在2个月和5个月后分别派发股息1元/股，该股票目前价格是30元/股，所有期限的无风险连续利率均为6%，某投资者持有该股票6个月期的远期合约空头。 3个月后，该股票价格涨到35元，无风险利率仍为6%，此时远期合约的空头价值是（）元。A-5.00
B-5.55
C-6.00
D-6.55
正确答案： D解析： 暂无解析 -
第21题：
单选题假设一只无红利支付的股票价格为20元/股，无风险连续利率为10%，该股票3个月后到期的远期价格为（）元/股。A19.51
B20.51
C21.51
D22.51
正确答案： D解析： 暂无解析 -
第22题：
单选题某股票预计在2个月和5个月后分别派发股息1元/股，该股票目前价格是30元/股，所有期限的无风险连续利率均为6%，某投资者持有该股票6个月期的远期合约空头。 该远期价格等于（）元。A28.19
B28.89
C29.19
D29.89
正确答案： B解析： 暂无解析 -
第23题：
单选题无风险资产收益率为7%，某股票A的预期收益率为15%，标准差为20%，如果由无风险资产和股票A构成的投资组合的预期收益率为13%，那么该组合的标准差为（）。A15%
B20%
C0
D17%
正确答案： A解析： 暂无解析