甲、乙、丙三条生产线生产某种零件,效率比为3:4:5,甲和乙生产线共同生产A订单,完成时甲比乙少生产250个。乙和丙共同生产B订单,完成时乙生产了720个。问A订单的零件个数比B订单:()A.少不到100个B.少100个以上C.多不到100个D.多100个以上

第1题：

第2题：

第3题：

答案：D

解析：

第4题：

答案：C

解析：

第一步，本题考查工程问题。
第二步，设乙单位时间内生产A的件数为1，B的件数为m，则甲生产A、B的效率分别为2、3m。要想两个企业尽快完成任务，且甲最终生产了1.5X件产品，则甲让负责生产B，生产完B之后再去帮乙完成A。则根据甲、乙所用的时间相等列方程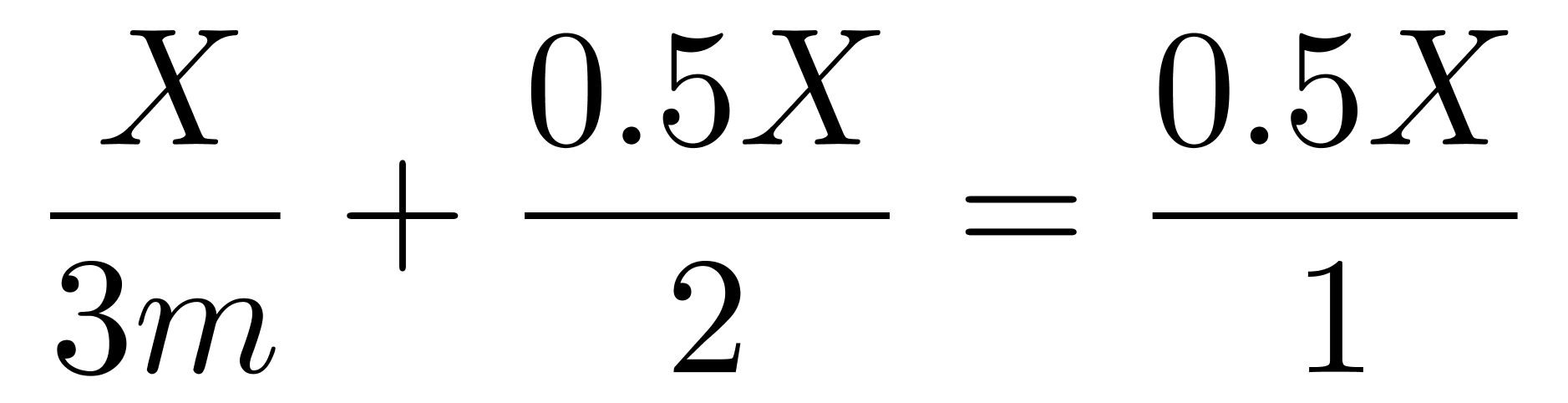：，化简可得m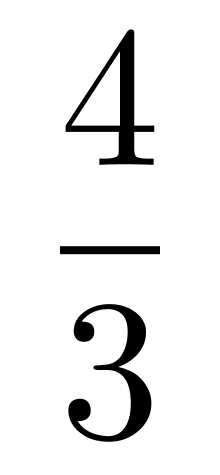＝，因此乙单位时间内生产A的件数与B的件数之比为1：m＝3∶4 。
因此，选择C选项。

第5题：

甲和乙两条自动化生产线同时生产相同的产品，甲生产线单位时间的产量是乙生产线的5倍，甲生产线每工作1小时就需要花3小时时间停机冷却而乙生产线可以不间断生产。问以下哪个坐标图能准确表示甲、乙生产线产量之差（纵轴L）与总生产时间（横轴T）之间的关系？

A.如上图所示
B.如上图所示
C.如上图所示
D.如上图所示

答案：A

解析：

第一步，本题考查工程与函数图形杂糅问题。
第二步，给出效率比例关系的工程问题，赋值效率。赋值乙生产线的效率即一小时的产量为1，则甲生产线的产量为5。函数图像采用描点法进行解题，列表分析如下：



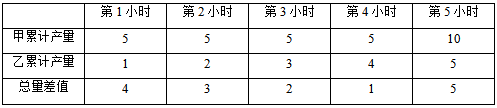
第三步，第1小时，总量差值为4，后续3个小时差值从4降到1，则第1小时的斜率＞后续3个小时，排除BC选项。第1小时和第5小时的差值分别为4和5，差距较小，观察AD选项，A选项更满足题干条件。
因此，选择A选项。

第6题：

第7题：

答案：A

解析：

本题属于工程问题。
解法一：由甲、乙产品共120件，可得：甲+乙=120①，由改造后生产时间比原来节省20%，可得：5×89%甲+6×75%乙=（5甲+6乙）×80%②，由①、②两式联立可得，甲=48，所以该任务要求生产48件甲产品。
因此，选择A选项。
解法二：本题可以用十字交叉法：

5甲：6乙=5:9，化简可得甲：乙=2:3，而甲乙的总和为120，所以甲=48。
因此，选择A选项。

第8题：

加工一批零件，甲单独完成需30天，乙单独完成需20天。现两人合作若干天后甲离开，乙继续加工，共用16天完成生产任务。问乙比甲多干了几天（）

• A、10
• B、8
• C、7
• D、6

第9题：

第10题：

第11题：

第12题：

第13题：

第14题：

答案：A

解析：

第15题：

第16题：

答案：C

解析：

第一步，本题考查工程问题。
第二步，设三者工作效率分别为甲、乙、丙，根据题意则有：2乙=甲+丙，3甲+3乙+7乙+7丙=7甲+7乙+7丙→3乙=4甲，赋值甲=3，则乙=4，解得丙=5。
第三步，B工程总量=10丙=10×5=50，即甲乙合作需要



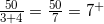
（天），即7天多。
因此，选择C选项。

第17题：

第18题：

第19题：

答案：A

解析：

本题考查的是工程问题。
效率提高后，单位时间内，甲车间能生产100×（1+5%）=105（件），乙车间能生产90×（1+10%）=99（件）。甲乙合作，单位时间效率和为105+99=204，共需要



个单位时间。每个单位时间甲车间比乙车间多生产105-99=6（件）产品，故25个单位时间，甲车间一共比乙车间多生产25×6=150（件）产品。
故本题的正确答案为A项。

第20题：

甲、乙、丙三个工厂承接A和B两批完全相同的加工订单，如果甲厂和乙厂负责A订单而丙厂负责B订单，则丙厂要比甲厂和乙厂晚15天完成;如在上述条件下甲厂分配1/3的生产资源或者乙厂分配1/5的生产资源用于B订单的生产，则A、B两个订单同时完成。问如果合并三个工厂的生产能力，第几天可以完成A订单的生产任务?

• A、22 
• B、24 
• C、25 
• D、26

第21题：

第22题：

第23题：