甲班与乙班同学同时从学校出发去某公园，甲班步行的速度是每小时4千米，乙班步行的速度是每小时3千米。学校有一辆汽车，它的速度是每小时48千米，这辆汽车恰好能坐一个班的学生。为了使这两班学生在最短的时间内到达，那么，甲班学生与乙班学生需要步行的距离之比是（ ）。 A. 15 : 11 B. 17: 22 C. 19 : 24 D. 21 : 27
题目
B. 17: 22
C. 19 : 24
D. 21 : 27
相似考题
更多“甲班与乙班同学同时从学校出发去某公园，甲班步行的速度是每小时4千米，乙班步行的速度是每小时3千米。学校有一辆汽车，它的速度是每小时48千米，这辆汽车恰好能坐一个班的学生。为了使这两班学生在最短的时间内到达，那么，甲班学生与乙班学生需要步行的距离之比是（ ）。 A. 15 : 11 B. 17: 22 C. 19 : 24 D. 21 : 27”相关问题
-
第1题：
甲班和乙班共有图书160本，甲班的图书是乙班的3倍，甲班和乙班各有图书多少本？
设甲有x本，乙有160-x本 x/（160-x）=3 x=480-3x 4x=480 x=120 甲120本，乙40本
-
第2题：
甲、乙两班学生到离校24千米的牧场去游玩，有一辆车一次只能乘坐一个班学生，甲、乙 两班步行与乘车交换进行，已知两班步行速度相同，汽车速度是步行速度的7倍，若甲班 先乘车，为使两班同时到达牧场，汽车应在距牧场多远处返回接乙班的学生？（ ）
A．4.8千米
B．7.2千米
C．8.1千米
D．9千米
正确答案：A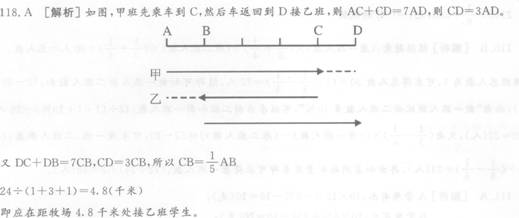
-
第3题：
两班工人的平均日产量的标准差系数分别为( )。
A．甲班11.44%
B．甲班8.41%
C．乙班12.51%
D．乙班9.89%
正确答案：BD
解析：甲班工人平均日产量的标准差系数；乙班工人平均日产量的标准差 -
第4题：
甲班与乙班同学同时从学校出发去某公园，甲班步行的速度是每小时4千米，乙班步行的速度是每小时3千米。学校有一辆汽车，它的速度是每小时48千米，这辆汽车恰好能坐一个班的学生。为了使这两班学生在最短的时间内到达，那么，甲班学生与乙班学生需要步行的距离之比是（ ）。A. 15 : 11
B. 17: 22
C. 19 : 24
D. 21 : 27答案：A解析：已知甲班步行的速度是每小时4千米，乙班步行的速度是每小时3千米，即甲的速度大于乙的速度，如果要使这两班学生在最短的时间内到达，则甲班的学生走的路程肯定要比乙班的多，答案中只有A是甲大于乙的，故选之。用常规方法解题，由題意可知：甲班到公园的距离等于乙班步行的距离加上乙班在车上行驶的距离，并且甲班到公园的时间等于乙班步行的时间加上乙班在车上行驶的时间，先设甲班步行距离为S，乙班步行的距离为D，则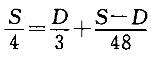
，求得S : D=15 : 11，故应选A。 -
第5题：
有两个班的学生从南部校区到北部校区参加活动，但只有一辆车接送。第一班的学生坐车从学校出发的同时，第二个班的学生开始步行。车到途中某处，让第一个班的学生下车步行，车立刻返回接第二班学生上车并直接开往北部校区，学生步行速度为每小时4公里，汽车载学生时车速每小时40公里，空车每小时50公里。问：要使两班学生同时到达北部校区，第二班学生要步行全程的（ ）。
答案：B解析：第一步，本题考查行程问题。
第二步，两班同学同时出发，同时到达，又两班学生的步行速度相同，说明两班学生步行的距离和坐车的距离分别相同。设两个班学生步行的距离为x，坐车距离为y，则由题意有x/4=y/40+（y-x）/50，解得x∶y=1∶6，那么x占全程的1/（1+6）=1/7，即第二班的学生步行了全程的七分之一。
因此，选择B选项。 -
第6题：
有两个班的小学生要到少年宫参加活动，但只有一辆车接送，第一班的学生坐车从学校出发的同时，第二班学生开始步行；车到途中某处，让第一班的学生下车步行，车立刻返回接第二班学生上车，并直接开往少年宫，学生步行速度为每小时4千米，载学生时车速每小时40千米，空车每小时50千米。问：要使两班学生同时到达少年宫，第一班学生步行了全程的几分之几？（学生上下车时间不计）（）
答案：D解析：根据题意，两个班的同学都是一段路步行一段路乘车，而乘车的速度比步行快，中间又没有停留，因此要同时到达少年宫，两个班的同学步行的路程一定要一样长。
如图所示，A是学校，B是少年宫，C是第一班学生下车的地点，D是第二班学生上车的地点。由题意得，AD=BC，学生步行的时间与车从A开到C再回到D的时间相等。设AD=BC=x，CD=y，则有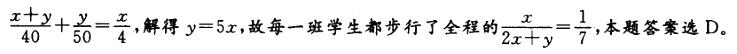
-
第7题：
张、王、李三人是某小学英语教师。他们对甲、乙两个班学生的学习英语状况作出如下判断()。
张：如果甲班所有学生都爱学英语。那么乙班有的学生不爱学英语
王：甲班有的学生不爱学英语.而乙班所有学生都爱学英语
李：或者甲班所有学生爱学英语，或者乙班所有学生爱学英语
如果上述三人的判断只有一假时。则以下各项中除了哪项其余判断均不能必然推出?()A.甲班所有学生都爱学英语,乙班所有学生都爱学英语
B.甲班有的学生不爱学英语，乙班有的学生不爱学英语
C.甲班有的学生不爱学英语,乙班所有学生都爱学英语
D.甲班所有学生都爱学英语，乙班有的学生不爱学英语答案：D解析：【知识点】教师基本能力——逻辑思维能力
首先设A=甲班所有学生都爱学英语，B=乙班所有学生都爱学英语。则三位老师的
话可表示为：张：A→非B;王：非A且B;李：A或者B。
如果王老师的话为真，则“非A”为真且“B”为真，由“B”为真可推出李老师的话为真.由“非A”为真可推出张老师的话为真，与“只有一假”矛盾，所以王老师的话为假。即其矛盾命题“A或非B”为真，李老师和张老师的话为真。
由“A或非B”和“A或者B”可知，A必然为真(因为非B和B至少有一个为假)，再由“A→非B”可知，“非B”为真。故答案选D。此题也可用代入法。 -
第8题：
甲乙两班同学学习一段材料，甲班同学学习不久就复习，乙班同学不复习：一周后，甲班同学的平均保持量是83％，乙班同学的平均保持量是25％。由此可见，防止遗忘要（ ）。A.集中复习
B.分散复习
C.及时复习
D.适度复习答案：C解析：C。解析：19世纪末德国心理学家艾宾浩斯的“遗忘曲线”提出，遗忘的进程不均衡，有先快后慢的特点。结合题干中甲乙两个班的同学有无及时复习产生的两种不同记忆保持量可知，防止遗忘应及时复习。 -
第9题：
某年级甲班、乙班各有男生50人。从两个班各抽取10人测量身高，并求其平均身高。如果甲班的平均身高大于乙班，能否推论甲班所有同学的平均身高大于乙班？为什么？
正确答案:不能。因为，从甲、乙两班分别抽取的10人，测量其身高，得到的分别是甲、乙两班的一个样本。样本的平均身高只是甲、乙两班所有同学平均身高的一个点估计值。即使是按随机化原则进行抽样，由于存在抽样误差，样本均数与总体均数一般很难恰好相等。因此，不能仅凭两个样本均数高低就作出两总体均数熟高熟低的判断，而应通过统计分析，进行统计推断，才能作出判断。 -
第10题：
甲乙两班同学学习一段材料，甲班同学学习不久就复习，乙班同学不复习；一周后，甲班同学的平均保持量是83%，乙班同学的保持量是25%。由此可见，防止遗忘要（）。
- A、集中复习
- B、分散复习
- C、及时复习
- D、适度复习
正确答案:C -
第11题：
单选题甲班与乙班同学同时从学校出发去某公园，甲班每小时步行4千米，乙班每小时步行3千米。学校有一辆汽车，它每小时步行48千米，这辆汽车恰好能坐一个班的学生。为了使这两班学生在最短的时间内到达，那么，甲班学生与乙班学生需要步行的距离之比是（ ）。A15:11
B17:22
C19:24
D21:27
正确答案： A解析：
方法一：要使两班学生最短时间到达，可使甲班同学先乘上车，到一定地点下车后继续前行，车回头接另外在路上走的乙班学生，最后同时到达目的地，则甲步行的时间加上坐车的时间与乙步行的时间加上坐车的时间相等。设全路段为x千米，甲走的路程为a，乙走的路程为b，则有a/4＋（x－a）/48＝b/3＋（x－b）/48，得a:b＝15:11。方法二：不通过计算而直接得到答案，甲的速度快，因此走的路程应该比乙多，只有15:11符合要求。 -
第12题：
单选题A甲班比乙班小
B甲班比乙班大
C甲班等于乙班
D不能确定
正确答案： C解析： -
第13题：
甲、乙两班同学同时去离学校12.1千米的陵园，甲班先乘车后步行，乙班先步行，当送甲班同学的车回来时乙即乘车前去。两班步行速度都是每小时5千米，车速度都是每小时40千米，已知两班同时到达陵园，那么甲在离陵园多远地方下车？（ ）
A．2千米
B．2.2千米
C．2.5千米
D．3千米
正确答案：B
甲、乙两班同时到达，表明两班乘车路程与步行路程分别相同。设甲班在离陵园x千米处下车改为步行，则有：
即甲班在离陵园2.2千米处下车改为步行。 -
第14题：
有甲乙丙三个班，如果从甲班调1名学生到乙班，甲乙两班人数相等。如果从乙班抽调1名学生到丙班就比乙班多2人，甲班和丙班相比，哪个班人多?多几人?（ ）
A．甲班与丙班人数相等
B．甲班比丙班多2人
C．甲班比丙班多1人
D．甲班比丙班少1人
正确答案：B
根据题意设甲乙丙三个班分别为x人，y人，z人，则x一1=y+1，y一1=z+1—2，解得x=z+2。正确答案为B。 -
第15题：
某学校有甲、乙两个班，原来甲班比乙班少20人，现在从乙班中抽调14人去甲班，则乙班是甲班的7/8，甲班原来有()人?A.50
B.53
C.55
D.60答案：A解析：
-
第16题：
A.甲班比乙班小
B.甲班比乙班大
C.甲班等于乙班
D.不能确定答案：A解析： -
第17题：
甲、乙两班的学生人数相等，各有一些学生参加选修课。甲班参加选修课的人数恰好是乙班没有参加的人数的1/3，乙班参加选修课的人数恰好是甲班没有参加的1/4.那么甲班没有参加的人数恰好是乙班没有参加人数的（ ）
A. 3/8
B. 2/3
C. 3/4
D. 8/9答案：D解析：解题指导： 设甲班未参加的有X人，乙未参加的有Y人 那么乙参加的有X/4，甲参加的有Y/3 因为二班人数相等，所以：X+Y/3=Y+X/4， 3/4X=2/3Y， X/Y=2/3/（3/4）=8/9， 即甲班没有参加人数是乙班没有参加人数的8/9，故答案为D。 -
第18题：
有两个班的小学生要到少年宫参加活动，但只有一辆车接送。第一班的学生坐车从学校出发的同时，第二班学生开始步行；车到途中某处，让第一班学生下车步行，车立刻返回接第二班学生上车并直接开往少年宫。学生步行速度为每小时4公里，载学生时车速每小时40公里，空车每小时50公里。那么，要使两班学生同时到达少年宫，第一班学生步行了全程的几分之几？（学生上下车时间不计）（）A. 1/7
B. 1/6
C. 3/4
D. 2/5答案：A解析：［解析］ 设由学校至少年宫的路程为线段AB，第一班学生坐车至C下车时，第二班学生恰行至D；空车返回至E恰与第二班学生相遇；此时第一班学生已由C行至F；第二班学生乘车由E行至B时，第一班学生也由F步行至B，两班学生同时到达少年宫。
依题意画出该路程图，不难看出：若以AB之中点M为中心，则A与B，D与F，E与C形成三组对称点。即AD=FB，DE=CF，从而AC=EB。运用对称性，可有如下解法：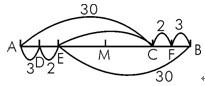
设AD=3，由于载人车速为人步行速之10倍，故AC=30，DC=27。由于空车速为人步行速之12.5倍，人与空车分别从D、C出发相向而行，至E相遇，故DE=2，EC=25。根据对称性知，CF=2，FB=3，AB=（2+3）×2+25=35。第一班学生步行之路程为CB=2+3=5，CB∶AB=5∶35=1/7。所以答案为A。 -
第19题：
甲乙两班同学学习一段材料，甲班同学学习后不久就复习，乙班同学不复习：一周后，甲班同学的平均保持量83%，乙班同学的保持量25%。由此可见，防止遗忘要__________。A.集中复习
B.分散复习
C.及时复习
D.适度复习答案：C解析： -
第20题：
某学校有甲、乙两个班，原来甲班比乙班少20人，现在从乙班中抽调14人去甲班，则乙班是甲班的
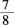
，甲班原来有( )人A.50
B.53
C.55
D.60答案：A解析：现在甲班比乙班多14x2-20=8人，则甲班现在有
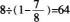
人，甲班原有64-14=50人，选择A。 -
第21题：
已知甲、乙两班学生统计学考试成绩：甲班平均分为70分，标准差为7.5分；乙班平均分为75分，标准差为7.5分。由此可知两个班考试成绩的离散程度（）
- A、甲班较大
- B、乙班较大
- C、两班相同
- D、无法作比较
正确答案:A -
第22题：
批量为500，其中甲班生产200件，乙班生产300件，按照分层按比例抽样方法抽取20件产品检测，则应从两班各抽取（）件
- A、甲班12件，乙班8件
- B、甲班8件，乙班12件
- C、甲班10件，乙班10件
- D、甲班6件，乙班14件
正确答案:B -
第23题：
单选题批量为500，其中甲班生产200件，乙班生产300件，按照分层按比例抽样方法抽取20件产品检测，则应从两班各抽取（）件。A甲班12件，乙班8件
B甲班8件，乙班12件
C甲班10件，乙班10件
D甲班6件，乙班14件
正确答案： D解析： 暂无解析 -
第24题：
问答题某年级甲班、乙班各有男生50人。从两个班各抽取10人测量身高，并求其平均身高。如果甲班的平均身高大于乙班，能否推论甲班所有同学的平均身高大于乙班？为什么？正确答案： 不能。因为，从甲、乙两班分别抽取的10人，测量其身高，得到的分别是甲、乙两班的一个样本。样本的平均身高只是甲、乙两班所有同学平均身高的一个点估计值。即使是按随机化原则进行抽样，由于存在抽样误差，样本均数与总体均数一般很难恰好相等。因此，不能仅凭两个样本均数高低就作出两总体均数熟高熟低的判断，而应通过统计分析，进行统计推断，才能作出判断。解析： 暂无解析