用长16厘米的铁丝围成各种长方形(长、宽均为整数,且长和宽不相等),围成的最大的一个长方形的面积是多少平方厘米?( ) A. 16 B. 15 C. 12 D. 9
题目
B. 15
C. 12
D. 9
相似考题
参考答案和解析
8 = 1 + 7→1X7=7;8 = 2 + 6→2X6 = 12;
8 = 3 + 5→3 X5=15;8 = 4 + 4→4 X 4 = 16;
8 = 5 + 3→5X3=15;8 = 6 + 2 → 6X2 = 12;
8 = 7 + 1→ 7X1=7。
我们发现当a从小到大取值,而b从大到小取值时,a与b的积呈现这样一个变化趋势:就是先由小到大,再由大到小,中间是最大的,也就是a与b取的数越接近,它们的乘积就越大。当a = b时,aXb的值最大。由此,得出一条规律:
如果a+b—定,只有当a =b时,a与b的乘积才最大。
由上面的讨论可知,在a +b=8,且a≠b中,当a=3,b= 5时,aXb的最大值是:3X5 = 15。 所以,所围成的最大的一个长方形的面积是15平方厘米。故本题正确答案为B。
更多“用长16厘米的铁丝围成各种长方形(长、宽均为整数,且长和宽不相等),围成的最大的一个长方形的面积是多少平方厘米?( ) A. 16 B. 15 C. 12 D. 9”相关问题
-
第1题:
某长方形的周长是44cm,若宽的3倍比长多6cm,则该长方形的长和宽各是多少?
-
第2题:
一个长方形的长减少5cm,宽增加2cm,就成为一个正方形,并且这两个图形的面积相等。这个长方形的长、宽各是多少
-
第3题:
用同样长的三根铁丝,分别围成长方形、正方形和圆形,它们的面积分别是ABC,则面积的大小关系为()。
A.B>C>A
B.C>B>A
C.A>B>C
D.B>A>C
正确答案:B
-
第4题:
用18厘米长的警戒线围成各种长方形,要求长和宽的长度都是厘米数,则围成的长方形的面积最大是多少?A.18平方厘米
B.20平方厘米
C.25平方厘米
D.40平方厘米答案:B解析:第一步,本题考查几何问题,属于几何特殊性质类。
第二步,由题意知长+宽=9厘米,要使长方形的面积尽可能大,则要求长和宽尽量接近,可使长=5厘米,宽=4厘米,此时面积最大,最大面积为4×5=20(平方厘米)。 -
第5题:
农户老张的田里有一堵16米长的围墙,老张想利用现有的围墙作为其中一边,修建一个长和宽均为整数米的长方形养鸡场,如老张手头的材料最多只能新修41米长的围墙,则他能围出的长方形养鸡场面积最大为( )平方米。A.195
B.204
C.210
D.256答案:A解析:
-
第6题:
国际篮联规定供国际比赛用的标准场地为( )。A.长26米,宽15米
B.长28米,宽16米
C.长28米,宽15米
D.长30米,宽16米答案:C解析:本题考查的是篮球比赛场地尺寸的知识点。
C项,比赛场地应是一块平坦、坚实且无障碍物的表面。其尺寸是长28米、宽15米,从界线的内沿丈量。综上,C正确。
A、B、D项,为干扰项。故排除。
故正确答案为C。 -
第7题:
用长16厘米的铁丝围成各种长方形(长、宽均为整数,且长和宽不相等),围成的最大的一个长方形的面积是多少平方厘米?( )
A. 16 B. 15 C. 12 D. 9答案:B解析:设长方形的长为a,宽为b,则这个问题就是求已知“a+b=8且a≠b时,aXb的最大值。为了便于观察,我们分析如下:8 = 1 + 7=>1X7 = 7;8 = 2 + 6=>2X6 = 12;
8 = 3 + 5=>3X5 = 15;8 = 4 + 4=>4X4 = 16;
8 = 5+3=>5X3 = 15;8 = 6 + 2=>6X2 = 12;
8 = 7 + 1=>7X1 = 7。
我们发现当a从小到大取值,而b从大到小取值时与b的积呈现这样一个变化趋势:就是先由小到大,再由大到小,中间是最大的,也就是a与b取的教越接近,它们的乘积就越大。当a = b时,aXb的值最大。由此,得出一条规律:
如果a+b一定,只有当a =b时,a与b的乘积才最大。
由上面的讨论可知,在a+b=8且a≠b时,当a = 3,b= 5时,aXb的最大值是:3X5 = 15。
所以,所围成的最大的一个长方形的面积是15平方厘米。故本题正确答案为B。 -
第8题:
用60米长的铁板围成一个长方形鸡窝,问这个鸡窝的面积最大是多少?()
- A、200
- B、225
- C、256
- D、258
正确答案:B -
第9题:
一个长方形苗圃的长是20米,宽是5米。一万米长的篱笆能围成多少个这样的苗圃?结果正确的是()
- A、200个
- B、2000个
- C、20个
正确答案:A -
第10题:
一个长方形长、宽分别为a、b。该长方形的面积为()。
- A、a+b
- B、a﹣b
- C、a/b
- D、ab
正确答案:D -
第11题:
单选题农户老张的田里有一堵16米的围墙。老张想利用现有的围墙作为其中的一边,修建一个长和宽均为整数的长方形养鸡场。如老张手头的材料最多只能新修41米长的围墙,则他能围出的长方形养鸡场面积最大为()平方米。A195
B204
C210
D256
正确答案: D解析: -
第12题:
单选题用60米长的铁板围成一个长方形鸡窝,问这个鸡窝的面积最大是多少?()A200
B225
C256
D258
正确答案: B解析: 暂无解析 -
第13题:
一个长方形的长是宽的2倍,写出这个长方形的面积与宽之间的函数关系式。
设:长方形的宽为x,面积为y,
则它的长为2x,
∴ y=x·2x=2x²
即面积与宽之间的函数关系式是:
y=2x²
-
第14题:
用长16厘米的铁丝围成各种长方形(长、宽均为整数,且长和宽不相等),围成最大的一个长方形面积是多少平方厘米?( )
A.16
B.15
C.12
D.9
正确答案:B设长方形的长为a,宽为b,则这个问题就是求已知a+b=8、且a≠b时,a×b的最大值。为了便于观察,我们分析如下:
8=1+7→1×7=7;8=2+6→2×6=12;
8=3+5→3×5=15;8—4+4→4×4=16;
8=5+3→5×3=15;8=6+2=6×2=12;
8=7+1=7×1=7。
我们发现当a从小到大取值,而b从大到小取值时,a与b的积呈现这样一个变化趋势:就是先由小到大,再由大到小,中间是最大的,也就是a与b取的数越接近,它们的乘积就越大。当a—b时,a×b的值最大。由此,得出一条规律:
如果a+b一定,只有当a—b时,a与b的乘积才最大。
由上面的讨论可知,在a十b=8,且a≠b中,当a=3,b=5时,a×b的最大值是:3×5=15。
所以,所围成的最大的一个长方形面积是l5平方厘米。故本题正确答案为B。 -
第15题:
一个长方形的长与宽的比是14:5,如果长减少l3厘米,宽增加l3厘米,则面积增加182平方厘米,那么原长方形面积是多少平方厘米?A.448
B.630
C.812
D.1120答案:B解析:设原长方形的长为l4a,宽为5a,由题意可得,(14a一l3)x(5a+13)=14a×5a+182,解得a=3,
原长方形面积是14×3×5×3=630平方厘米,应选择8。 -
第16题:
用长16厘米的铁丝围成各种长方形(长、宽均为整数,且长和宽不相等),围成的最大的一个长方形的面积是多少平方厘米?( )A. 16
B. 15
C. 12
D. 9答案:B解析:设长方形的长为a,宽为b,则这个问题就是求已知a+b=8、且a≠b时,axb的最大值。为了便于观察,我们分析如下:
8 = 1 + 7→1X7=7;8 = 2 + 6→2X6 = 12;
8 = 3 + 5→3 X5=15;8 = 4 + 4→4 X 4 = 16;
8 = 5 + 3→5X3=15;8 = 6 + 2 → 6X2 = 12;
8 = 7 + 1→ 7X1=7。
我们发现当a从小到大取值,而b从大到小取值时,a与b的积呈现这样一个变化趋势:就是先由小到大,再由大到小,中间是最大的,也就是a与b取的数越接近,它们的乘积就越大。当a = b时,aXb的值最大。由此,得出一条规律:
如果a+b—定,只有当a =b时,a与b的乘积才最大。
由上面的讨论可知,在a +b=8,且a≠b中,当a=3,b= 5时,aXb的最大值是:3X5 = 15。 所以,所围成的最大的一个长方形的面积是15平方厘米。故本题正确答案为B。 -
第17题:
如下图,大长方形被分为四个较小长方形,已知四个长方形的面积已标示出来,且这个大长方形的长和宽均为整数,那么图中双向箭头之间的部分是多长?( )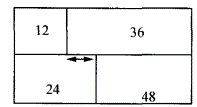 A. 1
A. 1
B. 2
C. 1 或 2
D. 3答案:C解析:
-
第18题:
某长方形长和宽的比是4:3,如果长减少4米,宽增加6米则变成一个正方形,原长方形的面积为(__)平方米?A. 900
B. 1200
C. 1500
D. 1800答案:B解析:本题考查基础几何问题。设长为4x,宽为3x,4x-4=3x+6,解得x=10,则长方形长40,宽30,面积为30*40=1200 -
第19题:
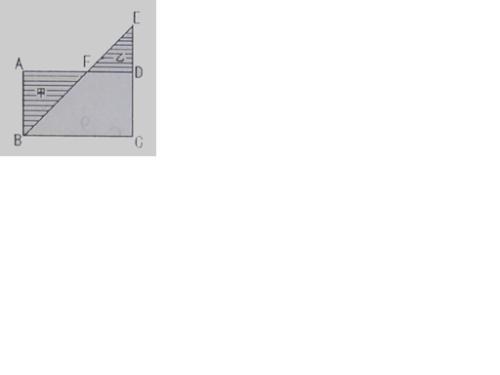
如下图,长方形的长为12厘米,宽为5厘米,阴影部分甲的面积比乙的面积大15平方厘米,那么,ED的长是:( )。
A. 2.8厘米
B. 2.5厘米
C. 3.4厘米
D. 3.5厘米答案:B解析:解题指导: 长方形面积为60cm,四边形BCDF面积为60-甲的面积:乙面积为甲的面积-15,三角形BCE面积为45cm,所以EC长为90÷12=7.5,故ED为2.5。故答案为B。 -
第20题:
用周长为18厘米的绳子,围成最大的长方形面积是()平方厘米。
- A、20
- B、32
- C、40
正确答案:A -
第21题:
24厘米长的绳子,围成的长方形面积最大是()平方厘米。
- A、36
- B、35
- C、32
正确答案:A -
第22题:
单选题一个长方形苗圃的长是20米,宽是5米。一万米长的篱笆能围成多少个这样的苗圃?结果正确的是()A200个
B2000个
C20个
正确答案: A解析: 暂无解析 -
第23题:
单选题农户老张的田里有一堵16米长的围墙。老张想利用现有的围墙作为其中的一边,修建一个长和宽均为整数米的长方形养鸡场。如老张手头的材料最多只能新修41米长的围墙,则他能围出的长方形养鸡场面积最大为多少平方米?A195
B204
C210
D256
正确答案: B解析: -
第24题:
单选题24厘米长的绳子,围成的长方形面积最大是()平方厘米。A36
B35
C32
正确答案: B解析: 暂无解析
