从1 到100 这一百个数字中任取一个,取出的数字能被2 或者被3 整除的概率是A.0.8B.0.67C.0.57D.0.4
题目
从1 到100 这一百个数字中任取一个,取出的数字能被2 或者被3 整除的概率是
A.0.8
B.0.67
C.0.57
D.0.4
相似考题
参考答案和解析
更多“从1 到100 这一百个数字中任取一个,取出的数字能被2 或者被3 整除的概率是”相关问题
-
第1题:
1到1000的整数(包含1和1000)中,至少能被2、3、5任意一个数整除的数共有(63)个。
A.668
B.701
C.734
D.767
正确答案:C
解析:这是一个典型的容斥原理的应用题。具体的解答思路如下。设A表示1到1000的整数(包含1和1000)中能够被2整除的数的集合;B表示1到1000的整数(包含1和1000)中能够被3整除的数的集合:C表示1到1000的整数(包含1和1000)中能够被5整除数的集合。则其中,符号表示对计算结果向下取整数。至少能被2、3、5任意一个数整除的数的个数为|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C|=500+333+200-166-100-66+33=734 -
第2题:
从2,3,4,5,6这五个数字中挑选两个,组成一个两位数,使其不能被3整除,则有多少种取法?
正确答案:14
-
第3题:
王老师在教授“2、3、5整除法”时,首先让班上同学任意提出一个数字,他都可以立即回答这个数能否被“2、3、5”整除。在热烈的氛围中,王老师再趁机提出,“大家想知道我为什么能一下子猜出数字是否能被整除吗?”随后进入整除法的教学。这种教学导入方式是()。A.故事导入法
B.衔接导人法
C.悬念导入法
D.直接导入法答案:C解析:悬念导入法是指在教学中,创设带有悬念性的问题来导入新的内容,给学生造成一种神秘感,从而激起学生的好奇心和求知欲的一种导入方法。 -
第4题:
从1,2,3,……,10共十个数字中任取一个,然后放回,先后取出5个数字,则所得5个数字全不相同的事件的概率等于()。A:0.3024
B:0.0302
C:0.2561
D:0.0285答案:A解析:该事件的概率=10*9*8*7*6/105=0.3024。 -
第5题:
一个三位数,百位的数字比十位的数字大而且都可以被3 整除,十位的数字和个位的数字都可以被2整除而且相加的值比百位大1,则这个三位数是( )。A.632
B.942
C.964
D.639答案:C解析:根据题目,百位的数字比十位的数字大而且都可以被3 整除,排除B;十位的数字和个位的数字都可以被2 整除,排除A、D,只剩余964,且满足十位个位相加值比百位大l,故选择C。 -
第6题:
从1.2.3.4.5.6.7.8.9这九个数字中,随机取出一个数字,这个数字是奇数的概率是() 答案:B解析:
答案:B解析: -
第7题:
从0,1,2,3,4,5中任取3个数字,组成能被3整除的无重复数字的3位数有( )个A.18
B.24
C.36
D.40
E.96答案:D解析:
-
第8题:
一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是l,3张卡片上的数
字是2,2张卡片上的数字是3,从盒中任取3张卡片。(1)求所取3张卡片上的数字完全相同的概率;(2)x表示所取3张卡片上的数字的中位数,求X的分布列和EX。答案:解析:
(2)中位数X可以取1,2,3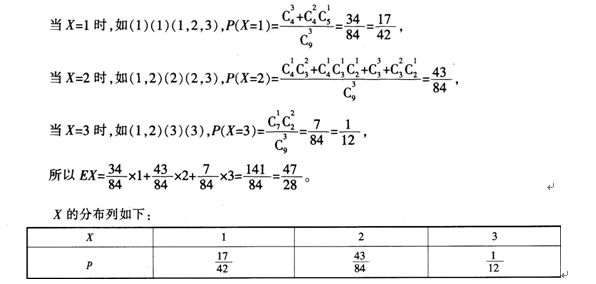
-
第9题:
编写一个Java程序,对于给定的年份,回答“Leap Year”(闰年)或者“Not a Leap Year”(平年)。如果一个年份能被4整除,但是不能被100整除,它是闰年;如果一个年份能被100整除,也能被400整除,它也是闰年。需要定义名为LeapYear的服务提供类

略 -
第10题:
从1,2,…,10共十个数字中任取一个,然后放回,先后取出5个数字,则所得5个数字全不相同的事件的概率等于()
正确答案:0.3024 -
第11题:
问答题35.从1,2.3,4,5中任取3个数字,则这3个数字中不含1的概率为正确答案:解析: -
第12题:
单选题在1,2,3,…,40中,至少要取出几个数,才能保证取出的数中一定有一个数能被4整除?()A3
B4
C21
D31
正确答案: D解析: 1,2,3,…,40中,能被4整除的有10个,因此最少要取出40-10+1=31个才能满足题干要求,选D。 -
第13题:
现有以下程序: Private Sub Command1 Click( ) c1=0 c2=0 For i=1 To 100 If i Mod 3=0 Then c1=c1+1 Else If i Mod 7=0 Then c2=c2+1 End If Next i Print c1+c2 End Sub 此程序运行后输出的是在1~100范围内( )。
A.同时能被3和7整除的整数个数
B.能被3或7整除的整数个数(同时被3和7整除的数只记一次)
C.能被3整除,而不能被7整除的整数个数
D.能被7整除,而不能被3整除的整数个数
正确答案:B
B。【解析】i是1到100的循环,在程序中,对3和7取模,显然就是3和7的倍数关系。需要注意的是If和else语句分别判断3和7的倍数而同时是21倍数的时候会不计,这有别于传统的计数方法。 -
第14题:
在所有的1位数中任取一个数,这个数能被2或3整除的概率为________。
A.1/2
B.3/4
C.7/10
D.4/5
正确答案:C
解析:设A={取出的数能被2整除}={0,2,4,6,8},B={取出的数能被3整除}={0,3,6,9},则有A+B={取出的数能被2或3整除}={0,2,3,4,6,8,9},所以P(A+B)=7/10。 -
第15题:
从1,2,…,10共十个数字中任取一个,然后放回,先后取出5个数字,则所得5个数字全不相同的事件概率等于()。A:0.3024
B:0.0302
C:0.2561
D:0.0285答案:A解析: -
第16题:
用1到7的数字组成一个六位数密码,密码中每个数字只使用一次,在所有可能的密码排列中,能被3整除的数字占所有可能的排列数的比重为:?
A1/6
B2/7
C3/7
D1/3答案:C解析:
-
第17题:
从0,2,4,6中取出3个数字,从1,3,5,7中取出两个数字,共能组成多少个没有重复数字且大于65000的五位数答案:解析:根据约束条件“大于65000的五位数”可知这样的五位数只有 7××××、65×××、67×××三种类型.
(1)能组成7××××型的五位数的个数是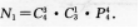
(2)能组成65×××型的五位数的个数是
(3)能组成67×××型的五位数的个数是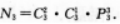
故所求的五位数的个数为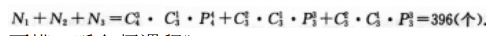
-
第18题:
从1到100的整数中任取一个数,则该数能被5或7整除的概率为( )A.0.02
B.0.14
C.0.2
D.0.32
E.0.34答案:D解析: -
第19题:
从标号1到10中的10张卡片中随抽2张,而它们的标号2种能被5整除的概率
 答案:A解析:
答案:A解析: -
第20题:
从1,2,…,10共十个数字中任取一个,然后放回,先后取出5个数字,则所得5个数字全不相同的事件的概率等于。A.0.3024
B.0.0302
C.0.2561
D.0.0285答案:A解析: -
第21题:
三段论:“因为3258的各位数字之和能被3整除,所以3258能被3整除”。前提是()
- A、 “3258能被3整除”是小前提
- B、 “3258的各位数字之和能被3整除”是大前提
- C、 “各位数字之和能被3整除的数都能被3整除” 是省略的大前提
- D、 “3258能被3整除”是大前提
正确答案:C -
第22题:
从数字1,2,…,10中有放回地任取4个数字,则数字10恰好出现两次的概率为()
正确答案:0.0486 -
第23题:
单选题三段论:“因为3258的各位数字之和能被3整除,所以3258能被3整除”。前提是()A“3258能被3整除”是小前提
B“3258的各位数字之和能被3整除”是大前提
C“各位数字之和能被3整除的数都能被3整除” 是省略的大前提
D“3258能被3整除”是大前提
正确答案: C解析: 暂无解析 -
第24题:
单选题从1,2,…,9共九个数字中任取一个数字,取出数字为偶数的概率为( ).A0
B1
C5/9
D4/9
正确答案: B解析: 9个数。偶数的个数是4个

