若有向图的邻接矩阵中，主对角线以下元素均为0， 则该图一定无环。

题目

若有向图的邻接矩阵中，主对角线以下元素均为0， 则该图一定无环。

相似考题

1.● 以下关于图及其存储结构的叙述中，正确的是 （41） 。（41）A. 无向图的邻接矩阵一定是对称的B. 有向图的邻接矩阵一定是不对称的C. 无向图采用邻接表存储更节省存储空间D. 有向图采用邻接表存储更节省存储空间

2.设图的邻接矩阵为图片,则该图为()。A、有向图B、无向图

3.如果某图的邻接矩阵时对角线元素均为零的上三角矩阵,则此图是( )。A、有向完全图B、连通图C、强连通图D、有向无环图

4.若有向图的邻接矩阵中，主对角线以下元素均为零，则该图的拓扑有序序列()。A、存在B、不存在C、不一定存在D、可能不存在

参考答案和解析
正确
更多“若有向图的邻接矩阵中，主对角线以下元素均为0， 则该图一定无环。”相关问题

  • 第1题：

    用相邻矩阵A表示图，判定任意两个顶点Vi和Vi，之间都有长度为m的路径相连，则只要检查(40)的第i行第j列的元素是否为0即可。

    从邻接矩阵可以看出，该图共有(41)个顶点。如果是有向图，该图有(42)条弧；如果是无向图，则共有(43)条边。

    A．mA

    B．A

    C．Am

    D．Am-1


    正确答案：C
    解析：(40)～(43)(40)要判断相邻矩阵A中任意两个顶点Vi和Vi之间是否有长度为m的路径相连，只要检查Am的第i行第j的元素是否为0即可，若为0则无，否则就存在。(41-43)邻接矩阵是表示顶点之间相邻关系的矩阵。设G=(V，E)是具有n个顶点的图，顶点序号依次为1，2，…，n，则G的邻接矩阵是n阶方阵，所以该图有3个顶点。如果此图是有向图，则矩阵中非0元素个数即为弧的数目(为4)；如果此图为无向图，则一条边会在矩阵中对应有两个非零元素出现，所以共有两条边。

  • 第2题：

    有一邻接矩阵

    如果是有向图，则该图共有(42)条弧；如果是无向图，则该图共有(43)条边。

    A．5

    B．4

    C．3

    D．2


    正确答案：B

  • 第3题：

    某图G的邻接矩阵如下所示。以下关于该图的叙述中，错误的是（ ）。

    A.该图存在回路（环）B.该图为完全有向图C.图中所有顶点的入度都大于0D.图中所有顶点的出度都大于0


    正确答案：B

  • 第4题：

    已知某图的邻接矩阵为对称矩阵，则该图一定为（ ）。

    A.有向图
    B.无向图
    C.完全图
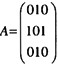
    D.强连通图

    答案：B
    解析：
    如图所示，一个无向图的邻接矩阵一定是对称的。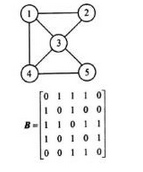

  • 第5题：

    无向图的邻接矩阵一定是对称矩阵，有向图的邻接矩阵一定是非对称矩阵。


    正确答案:错误

  • 第6题：

    若某无向图的邻接矩阵中共有10个值为1的元素，则说明此无向图中共有（）条无向边。


    正确答案:5

  • 第7题：

    证明：只要适当地排列顶点的次序，就能使有向无环图的邻接矩阵中主对角线以下的元素全部为0。


    正确答案:任意n个结点的有向无环图都可以得到一个拓扑序列。设拓扑序列为v0v1v2…vn-1，我们来证明此时的邻接矩阵A为上三角矩阵。证明采用反证法。
    假设此时的邻接矩阵不是上三角矩阵，那么，存在下标i和j（i>j），使得A[i][j]不等于零，即图中存在从vi到vj的一条有向边。由拓扑序列的定义可知，在任意拓扑序列中，vi的位置一定在vj之前，而在上述拓扑序列v0v1v2…vn-1中，由于i>j，即vi的位置在vj之后，导致矛盾。因此命题正确。

  • 第8题：

    若一个有向图的邻接矩阵中对角线以下元素均为零，则该图的拓扑序列必定存在。


    正确答案:正确

  • 第9题：

    判断题
    若一个有向图的邻接矩阵中，对角线以下元素均为0，则该图的拓扑有序序列必定存在。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第10题：

    判断题
    无向图的邻接矩阵一定是对称的，有向图的邻接矩阵一定是不对称的
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第11题：

    填空题
    若某无向图的邻接矩阵中共有10个值为1的元素，则说明此无向图中共有（）条无向边。

    正确答案： 5
    解析： 暂无解析

  • 第12题：

    单选题
    若一个有向图的邻接矩阵中，主对角线以下的元素均为零，则该图的拓扑有序序列（）。
    A

    存在

    B

    不存在

    C

    可能存在

    D

    无法判断


    正确答案： D
    解析：

  • 第13题：

    设某有向无环图的顶点个数为n、弧数为e，那么用邻接表存储该图时，实现上述拓扑排序算法的函数TopSort的时间复杂度是(6)。

    若有向图采用邻接矩阵表示(例如，图4-1所示有向图的邻接矩阵如图4-3所示)，且将函数TopSort中有关邻接表的操作修改为针对邻接矩阵的操作，那么对于有n个顶点、e条弧的有向无环图，实现上述拓扑排序算法的时问复杂度是(7)。


    正确答案：(6)O(n+e) (7)O(n2)
    (6)O(n+e) (7)O(n2) 解析：邻接表：对有n个顶点和e条弧的有向图而言，在拓扑排序中，若有向图无环，则每个顶点进出队列各一次，共执行e次，搜索算法时间复杂度是由n和e共同决定的，所以总的时间复杂度为O(n+e)。
    当用邻接矩阵：对于每个顶点，查找相邻边的时间复杂度是O(n)，一共有n个顶点，所以总的时间复杂度是O(n2)。

  • 第14题：

    以下关于图及其存储结构的叙述中，正确的是( )。

    A．无向图的邻接矩阵一定是对称的

    B．有向图的邻接矩阵一定是不对称的

    C．无向图采用邻接表存储更节省存储空间

    D．有向图采用邻接表存储更节省存储空间


    正确答案：A
    解析：邻接矩阵(Adjacency Matrix)是表示顶点之间相邻关系的矩阵。无向图的邻接矩阵一定是对称的，而有向图的邻接矩阵不一定对称。邻接表是图的一种链式存储结构。对图的每个顶点建立一个单链表(n个顶点建立n个单链表)，第i个单链表中的结点包含顶点Vi的所有邻接顶点，又称链接表。

  • 第15题：

    ●以下关于图的存储结构的叙述中，正确的是(43)。

    (43)A．有向图的邻接矩阵一定是对称的

    B．有向图的邻接矩阵一定是不对称的

    C．无向图的邻接矩阵一定是对称的

    D．无向图的邻接矩阵一定是不对称的


    正确答案：C

  • 第16题：

    若具有n个顶点、e条边且不带权的无向图采用邻接矩阵存储，则邻接矩阵中的零元素的数目是（）


    正确答案:n2-2e

  • 第17题：

    若一个有向图的邻接矩阵中，对角线以下元素均为0，则该图的拓扑有序序列必定存在。


    正确答案:正确

  • 第18题：

    若一个有向图的邻接矩阵中对角线以下元素均为零，则该图的拓扑有序序列必定存在。


    正确答案:正确

  • 第19题：

    无向图的邻接矩阵一定是对称的，有向图的邻接矩阵一定是不对称的


    正确答案:错误

  • 第20题：

    判断题
    若一个有向图的邻接矩阵中对角线以下元素均为零，则该图的拓扑序列必定存在。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第21题：

    判断题
    若一个有向图的邻接矩阵中对角线以下元素均为零，则该图的拓扑有序序列必定存在。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第22题：

    判断题
    无向图的邻接矩阵一定是对称矩阵，有向图的邻接矩阵一定是非对称矩阵。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第23题：

    问答题
    证明：只要适当地排列顶点的次序，就能使有向无环图的邻接矩阵中主对角线以下的元素全部为0。

    正确答案： 任意n个结点的有向无环图都可以得到一个拓扑序列。设拓扑序列为v0v1v2…vn-1，我们来证明此时的邻接矩阵A为上三角矩阵。证明采用反证法。
    假设此时的邻接矩阵不是上三角矩阵，那么，存在下标i和j（i>j），使得A[i][j]不等于零，即图中存在从vi到vj的一条有向边。由拓扑序列的定义可知，在任意拓扑序列中，vi的位置一定在vj之前，而在上述拓扑序列v0v1v2…vn-1中，由于i>j，即vi的位置在vj之后，导致矛盾。因此命题正确。
    解析： 暂无解析

  • 第24题：

    填空题
    若具有n个顶点、e条边且不带权的无向图采用邻接矩阵存储，则邻接矩阵中的零元素的数目是（）

    正确答案： n2-2e
    解析： 暂无解析

相关内容