现有20个均不等于7的正整数排成一行,其中,任意连续若干个数的和也不等于7,则这20个数之和的最小值为_______。
题目
相似考题
更多“现有20个均不等于7的正整数排成一行,其中,任意连续若干个数的和也不等于7,则这20个数之和的最小值为_______。 ”相关问题
-
第1题:
有四个不同的正整数,其中任意两个数之和是2的倍数,任意三个数的和是3的倍数,满足条件的最小的四个正整数之和是:
A.51
B.38
C.40
D.42
正确答案:C
首先这4个数必须同奇偶,其次这4个数必须对于3同余则4个数必须对6同余;又要最小则4个数中最小的是1,所以1、7、13、19是满足条件的最小的四个正整数,和为40。 -
第2题:
五个一位正整数之和为30,其中两个数为1和8,而这五个数和乘积为2520,则其余三个数为( )
A.6,6,9
B.4,6,9
C.5,7,9
D.5,8,8
正确答案:C
20.【解析】由结果是2520,个位数是0就可以知道这五个数中含5,2520÷5÷8=63 ,所以另外两个数为7和9。故选C。 -
第3题:
公务员考试题:从1,2,3,4,5,6,7,8,9中任意选出三个数,使它们的和为偶数,则共有( )种48.从1,2,3,4,5,6,7,8,9中任意选出三个数,使它们的和为偶数,则共有( )种不同的选法。
A.40 B.41 C.44 D.46
C 【解析】这是一个排列组合题。由题可知,三个数要么都为偶数,要么至少有两个奇数,三个奇数的情况是不存在的,所以计算公式为:P25+P34=5×4+4×3×2=20+24=44
-
第4题:
八个自然数排成一排,从第三个数开始,每个数都是它前面两个数的和,已知第五个数是7,则第八个数是( )。
A.11
B.18
C.29
D.47
正确答案:C
因为第五项是7,且第五项是第三、四项的和,所以第3、4项组合形式可能是1+6、6+1、2+5、5+2、3+4、4+3,然后逐项验证,可以发现:在保证第一、二项之和是第三项且各项之间没有重复数字出现的情况下,只有3+4这种情况符合要求。据此,可以推知:第六项为4+7=11,第七项为7+11=18,第八项为11+18=29。选C。 -
第5题:
有五个连续偶数,已知第三个数比第一个数与第五个数之和的1/4多18,则这五个偶数之和是( )
A.210 B.180 C.150 D.100
正确答案:B
设五个偶数分别是al,a2,a3,a4,a5,因为五个偶数是连续的,所以,第三个是第一个与第五个的和的1/2,即a3=(1/2)(a1+a5),又依题意,第三个数比第一个数与第五个数之和的1/4多18,所以a3=(1/4) (a1+a5)+18,即(1/2) (a1+a5)= (1/4)(a1+a5)+18,所以a1+a5=72,所以a3= 1/2×72=36,五个偶数的和是36x5=180。 -
第6题:
从1,2,3,……,30这30个数中,取出若干个数,使其中任意两个数的积都不能被4整 除。问最多可取几个数?A.14 个
B.15 个
C.16 个
D.17 个答案:C解析:最多取出所有15个奇数后再任取一个偶数能满足任意两个数的积不能被4整除,所以 最多可取16个数。 -
第7题:
有68个数排成一排,除头为两个数外,每个数的3倍恰好等于他两边两个数之和。经分析发现,这些数除以6所得的余数以12个数为周期重复出现。已知前两个数是0和1,则该数列最后一个数除以6的余数是()。
A. 2
B. 3
C. 4
D. 5答案:D解析:解题指导: 68/12=5余8 所以是5个周期后的第八个数 0,1,3,8,21,55,144,377 377/6=62余5,就是5。故答案为D。 -
第8题:
五个一位正整数之和为30,其中两个数为1和8,而这五个数和乘积为2520,则其余三个数为( )A. 6,6,9
B. 4,6,9
C. 5,7,9
D. 5,8,8答案:C解析:由结果是2520,个位数是0就可以知道这五个数中含5,2520/5/8=63 ,所以另外两个数为7和9。故答案为C。 -
第9题:
有4个数,前3个数成等差数列,后3个数成等比数列,且第一个数与第四个数之和是16,第二个数和第三个数之和是12,则这4个数的和为( )A.42
B.38
C.28
D.32
E.34答案:C解析:设第一个数为x,则第四个数为16-x,设第二个数为y,则第三个数为12-y。 -
第10题:
已知有一个数组intarr[7]={23,4,67,8,6,1,100};那么这个数组的最小值为()
- A、arr[1]
- B、arr[2]
- C、arr[5]
- D、arr[7]
正确答案:C -
第11题:
从1,2,3,…,30这30个数中,取出若干个数,使其中任意两个数的积都不能被4整除,问最多可取几个数()
- A、14个
- B、15个
- C、16个
- D、17个
正确答案:C -
第12题:
单选题有4个不同的自然数,他们当中任意两数的和是2的倍数,任意3个数的和是3的倍数,为了使这4个数的和尽可能小,则这4个数的和为()A40
B42
C46
D51
正确答案: D解析: 暂无解析 -
第13题:
从1,2,3,……,50这五十个数中,取出若干个数,使其中任意两个数的和都不能被7整除,则最多能取多少个数( )。
A. 21 B. 22C. 23 D. 29
从0开始,每7个数一组(0——6,7——13,......,42——48,共七组)中,最多可以选4个数(分别是除7余0,1,2,3的数)
所以,它们之中可以选7*4=28个数。
另外:0不包含在其中,要减去1个数;49和50两个数除7的余数分别是0和1,也要计算上,再加2个数。
故,最多共可取28-1+2=29个数 -
第14题:
有个学生在进行1、3、5、7、…若干连续奇数相加操作时,漏加了1个数,最后算得的和为2445。问漏掉了哪个数?
A.51
B.55
C.73
D.81
正确答案:B
[答案] B。[解析]首项为1的n项连续奇数列之和为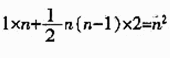 。因此,前50项的奇数之和为50×50=2500,49项的奇数之和为49×49=2401,2445正好在2401和2500之间,所以原数列应该是50项,漏掉的数为2500-2445=55。
。因此,前50项的奇数之和为50×50=2500,49项的奇数之和为49×49=2401,2445正好在2401和2500之间,所以原数列应该是50项,漏掉的数为2500-2445=55。
-
第15题:
利用等价类的划分,为判断其中任意两个数之和应大于第3个数是否为三角形的条件建立等价类表。
正确答案:等价类的划分通常可以分为以下几类: ①一个有效等价类和两个无效等价类。规定了输入数据的范围可以将输入数据划分为一个有效等价类和两个无效等价类。例如如果X输入的范围为1~50则有效等价类为“1≤X≤50”两个无效等价类为“X>50”或“X<1”。 ②若干有效等价类和一个无效等价类。 ③一个有效等价类和若干个无效等价类。如果规定了输入数据的范围则可以划分出一个有效等价类和若干个无效等价类。 ④在划分的某等价类中各值可以进一步划分成更小的等价类。如输入整数则可将输入的有效等价类划为负整数、零、正整数等价类。 三角形判断的等价类表如表11.1所示: 根据等价类表可设计如下测试用例:
a=3b=4c=5;(覆盖①、⑤)
a=1b=2c=6;(覆盖②)
a=-3b=2c=5;(覆盖③)
a=2b=2c=5;(覆盖④)
a=2b=3:(覆盖⑥)
a=1b=3c=5d=3;(覆盖⑦)
根据等价类表可设计如下测试用例:
a=3b=4c=5;(覆盖①、⑤)
a=1b=2c=6;(覆盖②)
a=-3b=2c=5;(覆盖③)
a=2b=2c=5;(覆盖④)
a=2b=3:(覆盖⑥)
a=1b=3c=5d=3;(覆盖⑦)
等价类的划分通常可以分为以下几类: ①一个有效等价类和两个无效等价类。规定了输入数据的范围,可以将输入数据划分为一个有效等价类和两个无效等价类。例如,如果X输入的范围为1~50,则有效等价类为“1≤X≤50”,两个无效等价类为“X>50”或“X<1”。 ②若干有效等价类和一个无效等价类。 ③一个有效等价类和若干个无效等价类。如果规定了输入数据的范围,则可以划分出一个有效等价类和若干个无效等价类。 ④在划分的某等价类中各值可以进一步划分成更小的等价类。如输入整数,则可将输入的有效等价类划为负整数、零、正整数等价类。 三角形判断的等价类表如表11.1所示: 根据等价类表可设计如下测试用例:
a=3,b=4,c=5;(覆盖①、⑤)
a=1,b=2,c=6;(覆盖②)
a=-3,b=2,c=5;(覆盖③)
a=2,b=2,c=5;(覆盖④)
a=2,b=3:(覆盖⑥)
a=1,b=3,c=5,d=3;(覆盖⑦)
根据等价类表可设计如下测试用例:
a=3,b=4,c=5;(覆盖①、⑤)
a=1,b=2,c=6;(覆盖②)
a=-3,b=2,c=5;(覆盖③)
a=2,b=2,c=5;(覆盖④)
a=2,b=3:(覆盖⑥)
a=1,b=3,c=5,d=3;(覆盖⑦)
-
第16题:
五个一位正整数之和为30,其中两个数是1和8,而这五个数的乘积为2520,则其余三个数为( )。
A.6,6,9
B.4,6,9
C.5,7,9
D.5,8,8
正确答案:C
[答案] C。解析:其余三个数的和为21,积为315,结合选项可直接选出。
-
第17题:
有五个连续偶数,已知第三个数比第一个数与第五个数之和的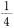 多18,则这五个偶数之和是( )。
多18,则这五个偶数之和是( )。
A. 210 B. 180 C. 150 D. 100答案:B解析:
-
第18题:
从1,2,3,……,30这30个数中,取出若干个数,使其中任意两个数的积都不能被4整除。问最多可取几个数?()A.14个
B.15个
C.16个
D.17个答案:C解析:任意两个数之积不能被4整除,即两个数分别不能被4整除,那么所取数中最多只能有一个偶数,且该偶数不能为4的倍数;共有15个奇数,所以最多可以取15+1=16个数。故正确答案为C。 -
第19题:
将一个正方形分成9个小正方形,填上1到9这9个自然数,使得任意一个横行,一个纵列以及每一对角线上的3个数之和等于15,请问位于中间的小正方形应填哪个数?
A. 4
B. 5
C. 6
D. 7答案:B解析:解题指导: 欲保证3个数之和都等于15,只有中间的数字为平均数5才可。故答案为B。 -
第20题:
自然数1~100排成两行,其中1~50为第一行,51~100为第二行,用长方形框出二行六个数,六个数之和为432,则这六个数中最小的是:A.46
B.44
C.66
D.68答案:A解析:第一步,本题考查基础计算问题。
第二步,设这六个数中最小的一个为x,则其他五个数为x+1,x+2,x+50,x+51,x+52,依题可得x+x+1+x+2+x+50+x+51+x+52=432,解得x=46。 -
第21题:
现有一个数据集合:2,3,3,3,3,4,4,4,5,6,6,7,7,7,其中众数为( )。A.2
B.3
C.4
D.5答案:B解析:样本的众数是样本中出现可能性最大的值,不过它不一定唯一。 -
第22题:
将C、C、E、E、I、N、S这7个字母随机地排成一行,恰好排成SCIENCE的概率为().
正确答案:1/1260 -
第23题:
单选题5个一位正整数的和为30,乘积为2520,其中两个数分别为1,8,则其余3个数为?A6,6,9
B4,6,9
C5,7,9
D5,8,8
正确答案: D解析:
