有6张卡片，分别写着数字1，2，5，6，8，9。现在从中取出3张卡片，并排放在一起，组成一个三位数。问可以组成多少个不同的偶数?( )A.144个 B.120个 C.60个 D.12个

题目

有6张卡片，分别写着数字1，2，5，6，8，9。现在从中取出3张卡片，并排放在一起，组成一个三位数。问可以组成多少个不同的偶数?(  )

A.144个            B.120个             C.60个              D.12个

相似考题

1.用0到9这10个数字,可以组成________个三位数。A．900B．826C．648D．568

2.字符A，B，C一次进入一个栈，按出栈的先后顺序组成不同的字符串，至多可以组成多少个不同的字符串?A．4B．6C．2D．5

3.有分别写着1，2，3，…，13的卡片各两张，任意抽出两张，计算这两张卡片上的数的积。这样得到许多不相等的积中，最多有多少个能被6整除？( )A． 18B．20C．21D．26

4.有这样四张卡片，每张卡片都是一面写着英文字母，另一面写着数字。已知第一张卡片一面写着字母“E”，另一面写着数字“4”；第二张卡片一面写着“G”，另一面写着“7”；第三张卡片有一面写着“F”；第四张卡片有一面写着“2”。由此可以推出（ ）。A．对这四张卡片而言，只要一面是辅音字母，另一面必定是奇数B．对这四张卡片而言，一面写着“F”的卡片，另一面必定写着“5”C．对这四张卡片而言，一面写着“2”的卡片，另一面必定是元音字母D．对这四张卡片而言，只要一面是元音字母，另一面必定是偶数

更多“有6张卡片，分别写着数字1，2，5，6，8，9。现在从中取出3张卡片，并排放在一起，组成一个三位数。问可以组成多少个不同的偶数?()A.144个B.120个C.60个D.12个”相关问题

  • 第1题：

    有五张卡片。他们的正反面分别写有0与1、2与3、4与5、6与7、8与9，将其中任意三张排放在一起组成三位数，共可组成多少个不同的三位数?

    A．360

    B．242

    C．336

    D．432


    正确答案：D
    先求出组成所有的三位数个数，再减去0在百位的个数。所以，共可组成不同的三位数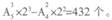

  • 第2题：

    表演者要分别做出三个不同题目的表演，评委用分别写有1、2、3、4的四张卡片给三个题目的表演评分，每次出示一张卡片，而且评委对这三个题目的表演从未拿出相同的卡片进行评判。那么表演者所有可能得分形式的卡片数字的和是多少?(  )

    A.240               B.180               C.120               D.80


     B. 这一问题等价于从1、2、3、4这四个数字每次抽出3个组成没有重复数字的三位数，求所有这些三位数的数字之和。根据对称性，分类有A33×（1+2+3）+A33×（1+2+4）+A33×（2+3+4）+A33×(3+4+1)=180（种）。

  • 第3题：

    用数字0、1、2、3、4、5可以组成没有重复数字，并且比20000大的五位偶数共有（ ）。 A．288个 B．240个 C．144个 D．126个


    正确答案：B
    根据题意可知，万位上的数字只能从2、3、4、5中选出。若万位上的数字为3或5，则个位上的数字为0、2、4中的任意一个，故共有＝144个；若万位上的数字为2或4，则个位上的数字为0、4中的任意一个或0、2中的任意一个，故共有＝96个。根据加法原理，比20000大的五位偶数共有144+96＝240个。故选B。

  • 第4题：

    有17个完全一样的信封，其中7个分别装了1元钱，8个分别装了10元钱，2个是空的，问最少需要从中随机取出几个信封，才能保证支付一笔12元的款项而无需找零？（ ）
    A．4 B．7 C．10 D．12


    答案：D
    解析：
    考虑最坏情况抽了8个10元的，2个空的，再抽2个1元的，所以最少取出8+2+2=12个才能保证。

  • 第5题：

    一个边长为8cm的立方体，表面涂满油漆，现在将它切割成边长为0．5cm的小立方体，问两个表面有油漆的小立方体有多少个?
    A．144 B．168 C．192 D．256


    答案：B
    解析：
    。 本题求两个表面有油漆的小立方体的个数，则符合要求的小立方体均分布在大立方体的12条棱的周围，每条棱可分8/0.5=16（段），即共有16个小立方体，又由于16个小立方体中，在每条棱的两端的两个小立方体三面有油漆，不符合题意，因此每条棱上只有14个小立方体，则两个表面有油漆的小立方体共有：12×14=168（个）。故本题选B。

  • 第6题：

    用数字0,1,2,3,4,5组成没有重复数字的四位数,其中三个偶数连在一起的四位数有多少个（ ）

    A.20
    B.28
    C.30
    D.36
    E.40

    答案：C
    解析：

  • 第7题：

    有20张卡片，每张卡片上分别标有0~20内的两个连续自然数，任取一张卡片，上面各位数字之和不小于14的概率为：


    答案：B
    解析：
    （0,1)-(6,7)这7张卡片上的各位数字之和小于14;(9,10)~(15,16)和（19,20)这8张

  • 第8题：

    用4、5、6三个数字可组成（）个不同的三位数。

    • A、4
    • B、6
    • C、8

    正确答案:B

  • 第9题：

    531工程中保证金的业务卡片不再从属于资金卡片。一个资金卡片可对应多个业务卡片，一个业务卡片也可关联多个资金卡片。


    正确答案:正确

  • 第10题：

    单选题
    一名儿童做加法游戏，在一个红口袋中装着20张分别标有数1，2，…，19，20的红卡片，从中任抽一张，把上面的数作为一个加数；在另一个黄口袋中装着10张分别标有数1，2，…，9，10的黄卡片，从中任取一张，把上面的数作为另一个加数，这名儿童一共可以列出加法式子（　　）．
    A

    30个

    B

    190个

    C

    200个

    D

    400个


    正确答案： B
    解析：
    本题为排列问题，共可列出加法式子的个数为20×10＝200.

  • 第11题：

    单选题
    用4、5、6三个数字可组成（）个不同的三位数。
    A

    4

    B

    6

    C

    8


    正确答案： C
    解析： 暂无解析

  • 第12题：

    多选题
    假设总体中有5个个体单位，从中随机抽取两个进行调查，则（    ）。
    A

    采用重置抽样，可以组成25个不同的样本

    B

    采用不重置抽样，可以组成25个不同的样本

    C

    采用重置抽样，可以组成10个不同的样本

    D

    采用不重置抽样，可以组成10个不同的样本

    E

    采用重置抽样与不重置抽样，可以组成的样本数相同


    正确答案： E,C
    解析：

  • 第13题：

    5，3，7三个数字可以组成几个三位数?（ ）。

    A．8个

    B．6个

    C．4个

    D．10个


    正确答案：B
    百位上的数可以在5，3，7三个数中选一个，有3种选法；在确定百位上的数后，十位上的数只有两种选法；百位上和十位上的数确定以后，个位上的数只有一种选法。所以三位数的组成方法共有3×2×1=6（种）。故正确答案为B。 

  • 第14题：

    有三张卡片的正反面分别写着1和2，4和6，7和8，用这三张卡片组成三位数，并且6可以当9用，则可得到不同的三位数的个数为：

    A．72

    B．120

    C．144

    D．240


    正确答案：A

  • 第15题：

    在五张卡片的正、反面上分别写有0与1，2与3，4与5，6与7，8与9，将其中任三张并排放在一起组成三位数，共可以组成多少个不同的三位数


    答案：
    解析：

  • 第16题：

    一个高使用率的四位密码门锁，为了防止他人从按键附着的指纹破解．怎样设置密码相对更安全?

    A.密码由两个不同的数字组成
    B.密码由三个不同的数字组成
    C.密码由四个不同的数字组成
    D.密码由三个或四个数字组成

    答案：B
    解析：
    若密码由四个不同的数字组成



    若密码由三个不同的数字组成，先选出两个重复数字所在数位然后排序



    若密码由两个不同的数字组成，分两种情况，三位重



    综上，密码由三个不同的数字组成最安全。

  • 第17题：

    从0，2，4，6中取出3个数字，从1，3，5，7中取出两个数字，共能组成多少个没有重复数字且大于65000的五位数


    答案：
    解析：
    根据约束条件“大于65000的五位数”可知这样的五位数只有 7××××、65×××、67×××三种类型．
    (1)能组成7××××型的五位数的个数是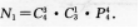

    (2)能组成65×××型的五位数的个数是

    (3)能组成67×××型的五位数的个数是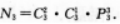

    故所求的五位数的个数为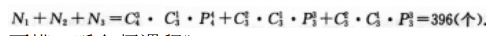

  • 第18题：

    由数字0、4、5、7可以组成多少个没有重复数字的偶数？（ ）

    A.25
    B.26
    C.27
    D.31

    答案：C
    解析：
    本题属于排列组合。
    整体分成两种情况，末位分别为0或者4，则可以组成的数字可能是1位，2位，3位，或者4位。
    1位时，只能是0和4，2种情况；2位时，情况数位：

    总个数位2＋5＋10＋10＝27。

  • 第19题：

    让1岁1个月～1岁6个月幼儿将水果放在水果卡片上配对，可以理解卡片的形象所代表的实际意义。


    正确答案:正确

  • 第20题：

    材料清单属于（）的一个组成部分。

    • A、工艺卡片
    • B、木模工艺结构图
    • C、铸造工艺图

    正确答案:A

  • 第21题：

    问答题
    桌子上有3张数字卡片，这几张卡片组成三位数字236。如果把这3张卡片变换一下位置或方向，就会组成另外一个三位数，而且这个三位数恰好能够被47整除。那么如何改变卡片的方位呢？这个三位数是多少呢？

    正确答案： 能够被47整除的三位数有94，141，188，235，282，329……要仔细得观察236这个数字，看怎么变动可以满足要求。可以将236中的23左右交换为32，再把6的那张卡片上下倒置变为“9”即可变为“329”，能够被47整除。
    解析： 暂无解析

  • 第22题：

    单选题
    在一个口袋中有10个黑球、6个白球、4个红球．问：至少从中取出多少个球，才能保证其中有白球？
    A

    14

    B

    15

    C

    17

    D

    18


    正确答案： B
    解析：

  • 第23题：

    单选题
    5，3，7三个数字可以组成几个三位数？（　　）
    A

    8个

    B

    6个

    C

    4个

    D

    10个


    正确答案： B
    解析：
    百位上的数可以在5，3，7三个数中选一个，有3种选法；在确定百位上的数后，十位上的数只有两种选法；百位上和十位上的数确定以后，个位上的数只有一种选法。所以三位数的组成方法共有3×2×1＝6种。

相关内容