求直线与平面相交，可以把它转化为求直线与平面内过 的直线相交。

题目

求直线与平面相交，可以把它转化为求直线与平面内过 的直线相交。

相似考题

1.下列关于直线与平面相交说法错误的一项是()。A.直线与平面相交后，交点是直线可见与不可见的分界点B.直线与平面相交的交点即在直线上又在平面上C.直线与平面相交有两个交点D.直线与平面相交后，直线便从平面的一侧到了平面的另一侧

2.平面与平面立体相交,其截交线是由()组成的封闭图形。A、直线B、曲线C、直线或曲线D、平面曲线

3.平面与平面相交为一直线,称为()。A.垂直线B.正垂线C.交线

4.平面与曲面立体相交,截交线为()。A、直线B、平面曲线或直线C、平面曲线D、空间曲线

更多“求直线与平面相交，可以把它转化为求直线与平面内过 的直线相交。”相关问题

  • 第1题：

    直线与平面相交时,可在该平面上作无数条直线与已知直线相交。()

    此题为判断题(对，错)。


    参考答案：对

  • 第2题：

    空间两条直线相交的定义指的是什么()

    A、在空间内不相交的两条直线

    B、分别位于两个不同平面内的两条直线

    C、某一平面内的一条直线与这个平面外的一条直线

    D、不再同一平面内的两条直线


    参考答案：D

  • 第3题：


    A.平行，但直线不在平面上
    B.直线在平面上
    C.垂直相交
    D.相交但不垂直

    答案：A
    解析：
    直线方向向量与平面法向量垂直，且直线上点不在平面内。

  • 第4题：

    直线 与平面π：x+y+z=2的位置关系

    A、平行
    B、相交但不垂直
    C、垂直
    D、直线f在平面上

    答案：B
    解析：
    由题意得：直线L的方向向量为m=(2，一l，一3)，平面霄的法向量即=(1，1，1)，易知m与，l不共线，且m·n#0，而直线l上的点(1，一l，2)在平面π上，故两者相交但不垂直。故选择B。

  • 第5题：

    下列说法正确的是（）

    • A、若一个平面内的相交二直线与另一个平面内的相交二直线对应平行，则此两平面平行。这是两平面平行的作图依据
    • B、两面平行的作图问题有：判别两已知平面是否相互平行；过一点作一平面与已知平面平行；已知两平面平行，完成其中一平面的投影
    • C、若相交两直线对应平行于属于另一平面的相交两直线，则此两平面平行
    • D、BC

    正确答案:A

  • 第6题：

    直线与平面相交有一个交点，其交点必是（）与（）的共有点，它既在直线上又在平面上，具有双重的从属关系。


    正确答案:直线与平面

  • 第7题：

    平面与曲面立体相交，截交线为（）。

    • A、直线
    • B、平面曲线或直线
    • C、平面曲线

    正确答案:B

  • 第8题：

    直线L：2x=5y=z-1与平面∏：4x-2z=5的位置关系是（）.

    • A、直线L与平面∏平行
    • B、直线L与平面∏垂直
    • C、直线L在平面∏上
    • D、直线L与平面∏相交，但不垂直

    正确答案:A

  • 第9题：

    若属于一平面的相交两直线对应平行于属于另一平面的相交两直线，则此两平面平行。


    正确答案:正确

  • 第10题：

    单选题
    平面与平面立体相交，其截交线是由（）组成的封闭图形。
    A

    直线

    B

    曲线

    C

    直线或曲线


    正确答案： A
    解析： 暂无解析

  • 第11题：

    单选题
    直线L1：2x=5y=z-1与平面∏：4x-2z=5的位置关系是（）．
    A

    直线L与平面∏平行

    B

    直线L与平面∏垂直

    C

    直线L在平面∏上

    D

    直线L与平面∏相交，但不垂直


    正确答案： C
    解析： 暂无解析

  • 第12题：

    判断题
    两一般位置平面相交，求交线步骤：1、用直线与平面求交点的方法求出两平面的两个共有点K、E。2、连接两个共有点，画出交线KE。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第13题：

    求直线与平面立体相交时的贯穿点不会用到的方法是()。

    A、利用立体表面的积聚性

    B、利用辅助平面

    C、利用直线的积聚性投影

    D、利用纬圆法和素线法


    答案：D

  • 第14题：

    关于辅助平面法求相贯线的投影,下面哪些说法是正确的()?

    A.辅助平面应该与相贯线相交或相切，也与两个相贯立体相交或相切

    B.辅助平面应该与相贯线相交，但不必要与两个相贯立体都相交

    C.辅助平面与相贯体产生的交线的投影应该尽可能简单好求，比如是直线或圆


    参考答案：AC

  • 第15题：

    两条直线是异面直线的充分条件是这两条直线（　　）

    A.分别在两个平面内．
    B.是分别在两个相交平面内的不相交的直线．
    C.是分别在两个相交平面内的不平行的直线．
    D.分别在两个相交平面内，其中一条与这两个平面的交线相交于一点，而另一条不过这个点．

    答案：D
    解析：

  • 第16题：


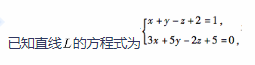
    平面Ⅱ的方程为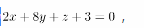

    则直线 与平面Ⅱ的位置关系是( )。


    A.平行
    B.直线在平面内
    C.垂直
    D.相交但不垂直

    答案：A
    解析：
    本题主要考查直线与平面的位置关系的判定。

  • 第17题：

    两一般位置平面相交，求交线步骤：1、用直线与平面求交点的方法求出两平面的两个共有点K、E。2、连接两个共有点，画出交线KE。


    正确答案:正确

  • 第18题：

    平面与平面立体相交，其截交线是由（）组成的封闭图形。

    • A、直线
    • B、曲线
    • C、直线或曲线

    正确答案:A

  • 第19题：

    设直线的方程为x=y-1=z，平面的方程为x-2y+z=0，则直线与平面（）。

    • A、重合
    • B、平行不重合
    • C、垂直相交
    • D、相交不垂直

    正确答案:B

  • 第20题：

    直线L1：2x=5y=z-1与平面∏：4x-2z=5的位置关系是（）．

    • A、直线L与平面∏平行
    • B、直线L与平面∏垂直
    • C、直线L在平面∏上
    • D、直线L与平面∏相交，但不垂直

    正确答案:A

  • 第21题：

    单选题
    若P是平面α外一点，则下列命题正确的是（　　）．
    A

    过P只能作一条直线与平面α相交

    B

    过P可作无数条直线与平面α垂直

    C

    过P只能作一条直线与平面α平行

    D

    过P可作无数条直线与平面α平行


    正确答案： D
    解析：
    过P可以作无数条直线与平面α相交；过P只能作一条直线与平面α垂直；过P可作无数条直线与平面α平行．

  • 第22题：

    单选题
    求直线与平面立体相交时的贯穿点不会用到的方法（）
    A

    利用立体表面的积聚性

    B

    利用辅助平面

    C

    利用直线的积聚性投影

    D

    利用纬圆法和素线法


    正确答案： A
    解析： 暂无解析

  • 第23题：

    判断题
    使用相交曲线（Intersection Curve）对两个平面求交，只要勾选上Associate选项，则这两个平面的相交直线必定与这两个平面相关。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第24题：

    单选题
    下列说法正确的是（）
    A

    若一个平面内的相交二直线与另一个平面内的相交二直线对应平行，则此两平面平行。这是两平面平行的作图依据

    B

    两面平行的作图问题有：判别两已知平面是否相互平行；过一点作一平面与已知平面平行；已知两平面平行，完成其中一平面的投影

    C

    若相交两直线对应平行于属于另一平面的相交两直线，则此两平面平行

    D

    BC


    正确答案： D
    解析： 暂无解析

相关内容