2、在单正态总体均值（方差未知)的区间估计时，以下因素中影响置信区间精度是（）。A．样本均值B．置信水平C．样本标准差D．样本量

题目

2、在单正态总体均值（方差未知)的区间估计时，以下因素中影响置信区间精度是（）。

A．样本均值

B．置信水平

C．样本标准差

D．样本量

相似考题

1.在方差未知时,正态均值μ的1-α置信区间长度与________。A．与α的大小有关B．样本量的平方根成反比C．总体标准差成正比D．样本标准差成正比

2.以下情况可以用Z统计量检验的有( )。A总体均值的检验，小样本B正态总体均值的检验，小样本，方差未知C大样本总体均值的检验D正态总体方差的检验

3.两个正态总体,方差未知,对两个总体均值之差进行区间估计时,以下说法正确的有()A.两个总体方差相等时，需要根据自由度为n1+n2-2的t分布进行区间估计B.两个总体方差不相等时，需要根据自由度为n1+n2-2的t分布进行区间估计C.进行区间估计时t分布的自由度与两个总体方差是否相等无关两个总体方差相等时，进行区间估计时t分布的自由度需要进行近似计算D.两个总体方差不相等时，进行区间估计时t分布的自由度需要进行近似计算

4.在方差未知时，正态均值μ的1-α置信区间长度与( )。A．样本均值成正比B．样本量n的平方根成反比C．总体标准差成正比D．样本标准差成正比E．α成正比

更多“2、在单正态总体均值（方差未知)的区间估计时，以下因素中影响置信区间精度是（）。”相关问题

  • 第1题：

    小样本情况下，总体服从正态分布，总体方差未知，总体均值在置信水平(1-a)下的置信区间为( )


    正确答案：A

  • 第2题：

    正态总体参数均值、方差、标准差的1-α置信区间为( )。


    正确答案：ABDE
    解析：室正态总体均值、方差、标准差的1-α置信区间如表1.4-1所示。

  • 第3题：

    总体为正态分布，σ2未知，则总体均值的1-σ置信区间是( )。


    正确答案：B
    解析：估计正态总体均值的置信区间，若σ未知，σ用其估计s代替，利用t分布，且是对称区间，故总体均值置信区间为。

  • 第4题：

    当正态总体的方差未知，且为小样本条件下，构造总体均值的置信区间使用的分布是（ ）。

    A.正态分布
    B.t分布
    C.x2分布
    D.F分布

    答案：B
    解析：
    如果总体方差未知，且为小样本条件下，需要用样本方差代替总体方差，样本均值经过标准化以后的随机变量服从自由度为(n-1)的t分布，需要采用t分布来建立总体均值的置信区间。

  • 第5题：

    下列表述中，错误的是（）。

    • A、总体均值的置信区间都是由样本均值加减估计误差得到
    • B、在小样本情况下，对总体均值的估计都是建立在总体服从正态分布的假定条件下
    • C、当样本量n充分大时，样本均值的分布近似服从正态分布
    • D、当总体服从正态分布时，样本均值不服从正态分布
    • E、对总体均值进行区间估计时，不需要考虑总体方差是否已知

    正确答案:D,E

  • 第6题：

    总体为正态分布、方差σ2未知。 样本量n = 20、样本的平均值为χ、标准差为 S ，当置信水平 为1-α时，总体均值μ的置信区间为（）。


    正确答案:χ±tα/2(20-1)S/√20

  • 第7题：

    如果正态总体均值95%置信区间为（960，1040），则有（）

    • A、样本容量为16
    • B、能给出置信下限的单侧置信区间为（966.33，+∞）
    • C、样本均值为1000
    • D、样本方差是81.63
    • E、容许误差是40

    正确答案:B,C,E

  • 第8题：

    设总体服从正态分布，方差未知，在样本容量和置信度保持不变的情形下，根据不同的样本值得到总体均值的置信区间长度将（）。

    • A、增加
    • B、不变
    • C、减少
    • D、都有可能

    正确答案:D

  • 第9题：

    以下问题可以用Z检验的有（）。

    • A、正态总体均值的检验，方差已知
    • B、正态总体均值的检验，方差未知
    • C、大样本下总体均值的检验
    • D、正态总体方差的检验

    正确答案:A,C

  • 第10题：

    单选题
    当正态总体的方差未知，且为小样本条件下，构造总体均值的置信区间使用的分布是（　　）。
    A

    正态分布

    B

    t分布

    C

    χ2分布

    D

    F分布


    正确答案： A
    解析：
    如果总体方差未知，且为小样本条件下，需要用样本方差代替总体方差，样本均值经过标准化以后的随机变量服从自由度为（n－1）的t分布，需要采用t分布来建立总体均值的置信区间。

  • 第11题：

    单选题
    有30个调查者分别对同一正态总体进行了随机抽样，样本量都是100，总体方差未知。调查者分别根据各自的样本数据得到总体均值的一个置信度90%的置信区间，这些置信区间中包含总体均值的区间有（）
    A

    30个

    B

    90个

    C

    27个

    D

    3个


    正确答案： B
    解析： 暂无解析

  • 第12题：

    判断题
    对方差未知的正态总体进行样本容量相同的n次抽样，则这n个置信区间的宽度必然相等。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第13题：

    大样本情况下，总体服从正态分布，总体方差已知，总体均值在置信水平(1-α)下的置信区间为（ ）


    正确答案：A

  • 第14题：

    正态总体标准差σ的1-α置信区间为( )(μ未知)。


    正确答案：D
    解析：σ2的估计常用样本方差s2，因此从s2的分布来构造置信区间。利用χ2(n-1)分布可以得到σ2的1-α置信区间为：，其中与分别是χ2(n-1)分布的分位数与分位数。将上式两边开平方，可得σ的1-α置信区间为。

  • 第15题：

    正态总体标准差σ的1 -a置信区间为（）（μ未知）。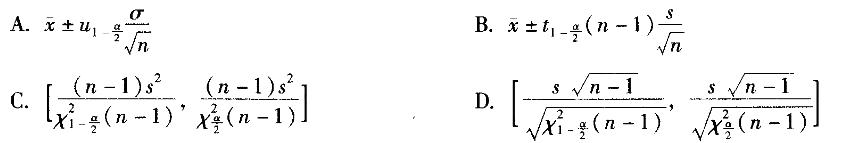


    答案：D
    解析：

  • 第16题：

    已知总体分布为正态，方差未知。从这个总体中随机抽取样本容量为65的样本，样本平均数 为60，样本方差为100，那么总体均值 的99%的置信区间为

    A.[ 56.775 ,63.225]
    B.[53.550,66.450]
    C.[56.080,63.920]
    D.[57.550,62.450]

    答案：A
    解析：
    本题考查的是总体平均数的估计方法。当总体方差未知时，若总体分布为正态，或者总体分布为非正态，但样本容量超过30，置信区间的公式是：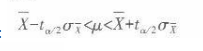

    因为总体方差未知，可通过如下公式计算标准误：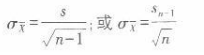

    当n>30时，t分布渐近正态分布，在不查表的情况下也可用

    作近似计算。将本题中各项数据代入，求得置信区间为[ 56.775，63.225]。因此本题选A。

  • 第17题：

    对方差未知的正态总体进行样本容量相同的n次抽样，则这n个置信区间的宽度必然相等。


    正确答案:错误

  • 第18题：

    有30个调查者分别对同一正态总体进行了随机抽样，样本量都是100，总体方差未知。调查者分别根据各自的样本数据得到总体均值的一个置信度90%的置信区间，这些置信区间中包含总体均值的区间有（）

    • A、30个
    • B、90个
    • C、27个
    • D、3个

    正确答案:C

  • 第19题：

    当正态总体的方差已知时，估计总体均值的置信区间使用的分布是（）。

    • A、正态分布
    • B、t分布
    • C、卡方分布
    • D、F分布

    正确答案:A

  • 第20题：

    下列场合适合于用t统计量的是（）。

    • A、总体正态大样本方差未知
    • B、总体非正态大样本方差未知
    • C、总体正态小样本方差未知
    • D、总体非正态小样本方差未知

    正确答案:C

  • 第21题：

    单选题
    当正态总体的方差未知，且为小样本条件下，构造总体均值的置信区间使用的分布是(　　)。
    A

    正态分布

    B

    t分布

    C

    x2分布

    D

    F分布


    正确答案： C
    解析：

  • 第22题：

    多选题
    θ是总体的一个待估参数，θL，θU是其对于给定α的1-α的置信下限与置信上限。则1-α置信区间的含义是（　　）。
    A

    所构造的随机区间[θL，θU]覆盖（盖住）未知参数θ的概率为1-α

    B

    由于这个随机区间随样本观测值的不同而不同，它有时覆盖住了参数θ，有时则没有覆盖参数θ

    C

    用这种方法做区间估计时，不能覆盖参数θ的机率相当小

    D

    如果P（θ＜θL）＝P（θ＞θU）＝α/2，则称这种置信区间为等尾置信区间

    E

    正态总体参数的置信区间是等尾置信区间，而比例p的置信区间不是等尾置信区间


    正确答案： C,E
    解析：
    C项，用这种方法做区间估计时，100次中大约有100（1-α）个区间能覆盖未知参数，不能说机率是大还是小，需要根据α的具体情况来确定；E项，正态总体参数的置信区间及比例p的置信区间都是等尾置信区间。

  • 第23题：

    多选题
    如果正态总体均值95%置信区间为（960，1040），则有（）
    A

    样本容量为16

    B

    能给出置信下限的单侧置信区间为（966.33，+∞）

    C

    样本均值为1000

    D

    样本方差是81.63

    E

    容许误差是40


    正确答案： D,B
    解析： 暂无解析

  • 第24题：

    填空题
    总体为正态分布、方差σ2未知。 样本量n = 20、样本的平均值为χ、标准差为 S ，当置信水平 为1-α时，总体均值μ的置信区间为（）。

    正确答案： χ±tα/2(20-1)S/√20
    解析： 暂无解析

相关内容