函数f(x)=10arctanx-3lnx的极大值是： A. 10arctan2-3ln2 B. 5/2π-3 C. 10arctan3-3ln3 D. 10arctan(1/3)

题目
函数f(x)=10arctanx-3lnx的极大值是：
A. 10arctan2-3ln2
B. 5/2π-3
C. 10arctan3-3ln3
D. 10arctan(1/3)

相似考题

1.● 某一类应用问题中，需要求正比例函数与反比例函数之和的极值。例如，正比例函数 4x 与反比例函数 9/x 之和用 f(x)表示， 即 f(x)=4x + 9/x， （x>0） ,那么函数 f(x) （63） 。（63）A. 没有极小值B. 在 x=1 时达到极大值C. 在 4x=9/x 时达到极小值D. 极大值是极小值的 9/4 倍

2.设两函数f(x)及g(x)都在x=a处取得极大值，则函数F(x)=f(x)g(x)在x=a处( )。A.必取极大值 B.必取极小值 C.不可能取极值 D.是否取极值不能确定

3.设f(x)是(-a，a)是连续的偶函数，且当0＜x＜a时，f(x)＜f(0)，则有结论( )。A.f(0)是f(x)在(-a，a)的极大值，但不是最大值 B.f(0)是f(x)在(-a，a)的最小值 C.f(0)是f(x)在(-a，a)的极大值，也是最大值 D.f(0)是曲线y=f(x)的拐点的纵坐标

4.设函数f(x)在内连续，其导函数的图形如图所示，则f(x)有(52)。A．一个极小值点和两个极大值点B．两个极小值点和一个极大值点C．两个极小值点和两个极大值点D．三个极小值点和一个极大值点

更多“函数f(x)=10arctanx-3lnx的极大值是： ”相关问题

  • 第1题：

    设函数f（x）在x=a的某个邻域内连续，且f（a）为极大值，则存在δ＞0，当x∈（a-δ，a+δ）时，必有（ ）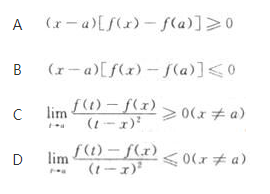


    答案：C
    解析：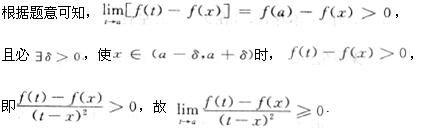

  • 第2题：

    设两函数f（x）及g（x）都在x=a处取得极大值，则F（x）=f（x）g（x）在x=a处（ ）

    A.必取极大值
    B.必取极小值
    C.不可能取极值
    D.是否取得极值不能确定

    答案：D
    解析：

  • 第3题：

    根据f(x)的导函数f'(x)的图像，判定下列结论正确的是（）


    A.在(－∞，－1)内，f(x)是单调增加的
    B.在(－∞，0)内，f(x)是单调增加的
    C.f(－1)为极大值
    D.f(－1)为极小值

    答案：D
    解析：
    x轴上方的f'(x)＞0，x轴下方的f'(x)＜0，即当x＜－1时，f'(x)＜0；当x＞－1时f'(x)＞0，根据极值的第一充分条件，可知f(－1)为极小值，所以选D．

  • 第4题：

    设函数y-f(x)连续，除x=a外f''(x)均存在。一一阶导函数y'=f(x)的图形如下，则y=f(x)


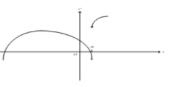    A.有两个极大值点，一个极小值点，一个拐点
    B.有一个极大值点，一个极小值点，两个拐点
    C.有一个极大值点，一个极小值点，一个拐点
    D.有一个极大值点，两个极小值点，两个拐点

    答案：D
    解析：




  • 第5题：

    函数y(x)的导函数f(x)的图象如图所示，Xo=-1，则( )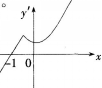

    A、X。不是驻点
    B、x。是驻点，但不是极值点
    C、x。是极小值点
    D、 X。极大值点

    答案：C
    解析：
    由图可知
    f，+(‰)>0，一(‰)<0且f(x)在x连续可导，故xo为极小值点。

  • 第6题：

    设函数f(x)=(1+x)ex，则函数f(x)（ ）

    A.有极小值
    B.有极大值
    C.既有极小值又有极大值
    D.无极值

    答案：A
    解析：
    【考情点拨】本题考查了函数极值的知识点.【应试指导】


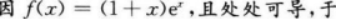
  • 第7题：

    设函数f（x，y）＝x3+y3-3xy，则（）。

    • A、f（0，0）为极大值
    • B、f（0，0）为极小值
    • C、f（1，1）为极大值
    • D、f（1，1）为极小值

    正确答案:D

  • 第8题：

    设f（x）在（-a，a）是连续的偶函数，且当0（）

    • A、f（0）是f（x）在（-a，A.的极大值，但不是最大值
    • B、B.f（0）是f（x）在（-a，的最小值
    • C、C.f（0）足f（x）在（-a，的极大值，也是最大值
    • D、f（0）是曲线y=f（x）的拐点的纵坐标

    正确答案:C

  • 第9题：

    单选题
    设函数f（x）满足关系式f″（x）＋[f′（x）]2＝x，且f′（0）＝0，则（　　）。
    A

    f（0）是f（x）的极大值

    B

    f（0）是f（x）的极小值

    C

    点（0，f（0））是曲线y＝f（x）的拐点

    D

    f（0）不是f（x）的极值，点（0，f（0））也不是曲线y＝f（x）的拐点


    正确答案： B
    解析：
    已知f″（x）＋[f′（x）]2＝x，方程两边对x求导得f‴（x）＋2f″（x）·f′（x）＝1，由f′（0）＝0，则f″（0）＝0，f‴（0）＝1，故在点x＝0的某邻域内f″（x）单调增加，即f－″（0）与f＋″（0）符号相反，故点（0，f（0））是曲线y＝f（x）的拐点。

  • 第10题：

    单选题
    若f（x）和g（x）在x＝x0处都取得极小值，则函数F（x）＝f（x）＋g（x）在x＝x0处（　　）
    A

    必取得极小值

    B

    必取得极大值

    C

    不可能取得极值

    D

    可能取极大值，也可能去极小值


    正确答案： A
    解析：
    根据极值的定义可知
    ∃δ1＞0使x∈（x0－δ1，x0＋δ1）时，f（x）＞f（x0）；
    ∃δ2＞0使x∈（x0－δ2，x0＋δ2）时，g（x）＞g（x0）；
    取δ＝min[δ1，δ2]，则x∈（x0－δ，x0＋δ）时，有f（x）＋g（x）＞f（x0）＋g（x0），即F（x）＝f（x）＋g（x）在x＝x0处取得极小值。

  • 第11题：

    单选题
    函数f（x）=10arctanx-3lnx的极大值是（）
    A

    10arctan2-31n2

    B

    （5／2）π-3

    C

    10arctan3-3ln3

    D

    10arctan（1／3）


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    设f（x）在（-a，a）是连续的偶函数，且当0（）
    A

    f（0）是f（x）在（-a，A.的极大值，但不是最大值

    B

    B.f（0）是f（x）在（-a，的最小值

    C

    C.f（0）足f（x）在（-a，的极大值，也是最大值

    D

    f（0）是曲线y=f（x）的拐点的纵坐标


    正确答案： B
    解析： 暂无解析

  • 第13题：

    设函数f(x)在x=a的某个邻域内连续，且f(a)为其极大值，则存在δ＞0，当x∈(a-δ，a+δ)时，必有( )。

    A.(x-a)[f(x)-f(a)]≥0
    B.(x-a)[f(x)-f(a)]≤0
    C.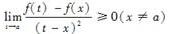
    D.

    答案：C
    解析：

  • 第14题：

    函数f（x）= 10arctanx-3lnx的极大值是：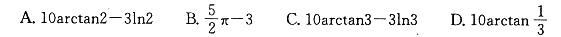


    答案：C
    解析：
    提示：函数的定义域(0，+∞)，求驻点，用驻点分割定义域，确定极大值。计算如下：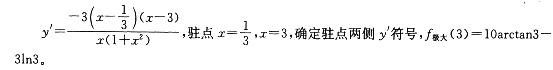

  • 第15题：

    设函数f(x)在x＝1处可导，且f'(1)＝0，若f"(1)＞0，则f(1)是（）

    A.极大值
    B.极小值
    C.不是极值
    D.是拐点

    答案：B
    解析：
    由极值的第二充分条件可知，应选B．

  • 第16题：

    设函数y=f（x）的导函数，满足f′（一1）=0，当x＜-l时，f′（x）＜0；当x＞-l时，f′（x）＞0.则下列结论肯定正确的是（ ）.《》（ ）

    A.x=-1是驻点，但不是极值点
    B.x=-1不是驻点
    C.x=-1为极小值点
    D.x=-1为极大值点

    答案：C
    解析：

  • 第17题：

    设f(x)在(-a,a)是连续的偶函数,且当0
    A. f(0)是f(x)在(-a，a)的极大值，但不是最大值
    B. f(0)是f(x)在(-a,a)的最小值
    C. f(0)是f(x)在(-a,a)的极大值，也是最大值
    D. f(0)是曲线y=f(x)的拐点的纵坐标


    答案：C
    解析：
    提示：f(x)是偶函数，当-a

  • 第18题：

    点（2，-2）是函数f（x，y）=x（4―x）―y（y+4）的（）。

    • A、极小值点
    • B、非极值点
    • C、非极值驻点
    • D、极大值点

    正确答案:D

  • 第19题：

    函数f（x）=10arctanx-3lnx的极大值是（）

    • A、10arctan2-31n2
    • B、（5／2）π-3
    • C、10arctan3-3ln3
    • D、10arctan（1／3）

    正确答案:C

  • 第20题：

    多元函数F（X）在X*处存在极大值的充分必要条件是：在X*处的Hessian矩阵（）。

    • A、等于零
    • B、大于零
    • C、负定
    • D、正定

    正确答案:C

  • 第21题：

    填空题
    函数y＝x3－3x的极大值点是____，极大值是____。

    正确答案： x=-1,y=2
    解析：
    将y＝x3－3x两边对x求导，得y′＝3x2－3，令y′＝0得x＝±1；y″（－1）＝－6＜0，则极大值点是x＝－1，此时y＝2。

  • 第22题：

    单选题
    设两函数f（x）及g（x）都在x＝a处取得极大值，则F（x）＝f（x）g（x）在x＝a处（　　）
    A

    必取极大值

    B

    必取极小值

    C

    不可能取极值

    D

    是否取得极值不能确定


    正确答案： D
    解析：
    本题采用举例法进行排除较为简单。
    令f（x）＝g（x）＝－|x|，f（x）与g（x）都在x＝0处取得极大值，但是f（x）g（x）＝x2在x＝0处取到极小值，故A、C项错误；
    令f（x）＝1－x2，g（x）＝－x2，则f（x）与g（x）都在x＝0处取得极大值，分别是1和0，f（x）g（x）＝x4－x2在x＝0处取得极大值0，故B项错误。

  • 第23题：

    单选题
    设函数z＝f（x，y）的全微分为dz＝xdx＋ydy，则点（0，0）（　　）。
    A

    不是f（x，y）的连续点

    B

    不是f（x，y）的极值点

    C

    是f（x，y）的极大值点

    D

    是f（x，y）的极小值点


    正确答案： D
    解析：
    函数的全微分为dz＝xdx＋ydy，则∂z/∂x＝x，∂z/∂y＝y，故∂2z/∂x2|（0，0）＝1＝A，∂2z/∂x∂y|（0，0）＝0＝B，∂2z/∂y2|（0，0）＝1＝C，又∂z/∂x|（0，0）＝0，∂z/∂y|（0，0）＝0，则B2－AC＝－1＜0，A＞0。故（0，0）是函数f（x，y）的极小值点。

相关内容