设f(x)是(-a,a)是连续的偶函数,且当0<x<a时,f(x)<f(0),则有结论( )。A.f(0)是f(x)在(-a,a)的极大值,但不是最大值 B.f(0)是f(x)在(-a,a)的最小值 C.f(0)是f(x)在(-a,a)的极大值,也是最大值 D.f(0)是曲线y=f(x)的拐点的纵坐标
题目
B.f(0)是f(x)在(-a,a)的最小值
C.f(0)是f(x)在(-a,a)的极大值,也是最大值
D.f(0)是曲线y=f(x)的拐点的纵坐标
相似考题
更多“设f(x)是(-a,a)是连续的偶函数,且当0<x<a时,f(x)<f(0),则有结论( )。”相关问题
-
第1题:
设函数f(x)在x=a的某个邻域内连续,且f(a)为极大值,则存在δ>0,当x∈(a-δ,a+δ)时,必有( )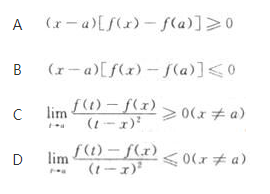 答案:C解析:
答案:C解析: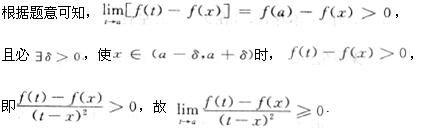
-
第2题:
设函数f(x)在点x=a处可导,则函数|f(x)|在点x=a处不可导的充分条件是( )A.f(a)=0且f′(a)=0
B.f(a)=0且f′(a)≠0
C.f(a)>0且f′(a)>
D.f(a)<0且f′(a)<答案:B解析: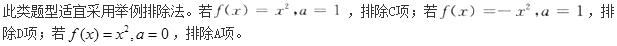
-
第3题:
设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f'(x)>0, f''(x)>0,则在(-∞,0)内必有:
A. f'(x)>0, f''(x)>0 B.f'(x)<0, f''(x)>0
C. f'(x)>0, f''(x)<0 D. f'(x)<0, f''(x)<0答案:B解析:提示:已知f(x)在(-∞,+∞)上是偶函数,函数图像关于y轴对称,已知函数在(0,+∞),f'(x)>0, f''(x)>0,表明在(0,+∞)上函数图像为单增且凹向,由对称性可知,f(x)在(-∞,0)单减且凹向,所以f'(x)<0, f''(x)>0。 -
第4题:
设f(x)是R上的可导函数,且f(x)>0。若f′(x)-3x---2f(x)=0,且f(0)=1,求f(x)。答案:解析: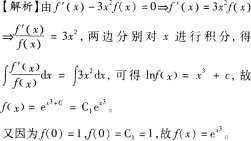
-
第5题:
设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f'(x)>0,f''(x)>0,则在(-∞,0)内必有( )。
A. f'(x)>0,f''(x)>0 B. f(x) 0
C. f'(x)>0,f''(x)答案:B解析:提示:f(x)在(-∞,+∞)上是偶函数,f'(x)在(-∞,+∞)在上是奇函数,f''(x)在(-∞,+∞)在上是偶函数,故应选B。 -
第6题:
设偶函数f(x)在区间(-1,1)内具有二阶导数,且f″(0)=f′(0)+1,则f(0)为f(x)的一个极小值。
正确答案:正确 -
第7题:
设f(x)在(-a,a)是连续的偶函数,且当0()
- A、f(0)是f(x)在(-a,A.的极大值,但不是最大值
- B、B.f(0)是f(x)在(-a,的最小值
- C、C.f(0)足f(x)在(-a,的极大值,也是最大值
- D、f(0)是曲线y=f(x)的拐点的纵坐标
正确答案:C -
第8题:
设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f'(x)>0,f"(x)>0,则在(-∞,0)内必有()。
- A、f'(x)>0,f"(x)>0
- B、f'(x)<0,f"(x)>0
- C、f'(x)>O,f"(x)<0
- D、f'(x)<0,f"(x)<0
正确答案:B -
第9题:
单选题(2008)设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f′(x)>0,f″(x)>0则在(-∞,0)内必有:()Af′(x)>0,f″(x)>0
Bf′(x)<0,f″(x)>0
Cf′(x)>0,f″(x)<0
Df′(x)<0,f″(x)<0
正确答案: C解析: 暂无解析 -
第10题:
单选题设在区间(-∞,+∞)内函数f(x)>0,且当k为大于0的常数时有f(x+k)=1/f(x)则在区间(-∞,+∞)内函数f(x)是( )。A奇函数
B偶函数
C周期函数
D单调函数
正确答案: C解析:
对该函数由f(x+2k)=1/f(x+k)=f(x),故f(x)是周期函数。 -
第11题:
单选题设f′(x0)=f″(x0)=0,f‴(x0)>0,且f(x)在x0点的某邻域内有三阶连续导数,则下列选项正确的是( )。Af′(x0)是f′(x)的极大值
Bf(x0)是f(x)的极大值
Cf(x0)是f(x)的极小值
D(x0,f(x0))是曲线y=f(x)的拐点
正确答案: D解析:
已知f‴(x0)>0,则f″(x)在x0点的某邻域内单调增加,又由f″(x0)=0,则在x0点的某邻域内f-″(x0)与f+″(x0)符号相反,故(x0,f(x0))是曲线y=f(x)的拐点。 -
第12题:
单选题设f(x)在(-a,a)是连续的偶函数,且当0()Af(0)是f(x)在(-a,A.的极大值,但不是最大值
BB.f(0)是f(x)在(-a,的最小值
CC.f(0)足f(x)在(-a,的极大值,也是最大值
Df(0)是曲线y=f(x)的拐点的纵坐标
正确答案: B解析: 暂无解析 -
第13题:
设函数f(x)在x=a的某个邻域内连续,且f(a)为其极大值,则存在δ>0,当x∈(a-δ,a+δ)时,必有( )。A.(x-a)[f(x)-f(a)]≥0
B.(x-a)[f(x)-f(a)]≤0
C.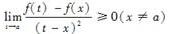
D. 答案:C解析:
答案:C解析:
-
第14题:
设函数 f (x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有 f ' (x) >0, f '' (x) >0,
则在(- ∞ ,0)内必有:
(A) f ' > 0, f '' > 0 (B) f ' 0
(C) f ' > 0, f ''答案:B解析:解:选 B。
偶函数的导数是奇函数,奇函数的导数是偶函数。
f (x)是偶函数,则 f '(x)是奇函数,当x > 0时, f '(x) > 0,则x f '(x)是奇函数,则 f ''(x)是奇函数,当x > 0时, f '(x) > 0,则x 0;
点评:偶函数的导数是奇函数,奇函数的导数是偶函数。 -
第15题:
设函数f(x)具有二阶导数,g(x)=f(0)(1-x)+f(1)x,则在区间[0,1]上
A.A当f'(x)≥0时,f(x)≥g(x)
B.当f'(x)≥0时,f(x)≤g(x)
C.当f"(x)≥0时,f(x)≥g(x)
D.当f"(x)≥0时,f(x)≤g(x)答案:D解析:由于g(0)=f(0),g(1)=f(1),则直线y=f(0)(1-x)+f(1)x过点(0,f(0))和(1,f(1)),当f"(x)≥0时,曲线y=f(x)在区间[0,1]上是凹的,曲线y=f(x)应位于过两个端点(0,f(0))和(1,f(1))的弦y=f(0)(1-x)+f(1)x的下方,即f(x)≤g(x)故应选(D).
(方法二)令F(x)=f(x)-g(x)=f(x)-f(0)(1-x)-f(1)x,
则 F'(x)=f'(x)+f(0)-f(1),F"(x)=f"(x).当f"(x)≥0时,F"(x)≥0,则曲线y=F(x)在区间[0,1]上是凹的.又F(0)=F(1)=0,从而,当x∈[0,1]时F(x)≤0,即f(x)≤g(x),故应选(D).
(方法三)令F(x)=f(x)-g(x)=f(x)-f(0)(1-x)-f(1)x,
则 F(x)=f(x)[(1-x)+x]-f(0)(1-x)-f(1)x
=(1-x)[f(x)-f(0)]-x[f(1)-f(x)]
=x(1-x)f'(ξ)-x(1-x)f'(η) (ξ∈(0,x),η∈(x,1))
=x(1-x)[f'(ξ)-f'(η)]
当f"(x)≥0时,f'(x)单调增,f'(ξ)≤f'(η),从而,当x∈[0,1]时F(x)≤0,即f(x)≤g(x),故应选(D). -
第16题:
设f(x)在(-a,a)是连续的偶函数,且当0
A. f(0)是f(x)在(-a,a)的极大值,但不是最大值
B. f(0)是f(x)在(-a,a)的最小值
C. f(0)是f(x)在(-a,a)的极大值,也是最大值
D. f(0)是曲线y=f(x)的拐点的纵坐标答案:C解析:提示:f(x)是偶函数,当-a -
第17题:
设f(x)是连续函数,F(x)是f(x)的原函数,则()。
A.当f(x)是奇函数时,F(x)必是偶函数
B.当f(x)是偶函数时,F(x)必是奇函数
C.当f(x)是周期函数时,F(x)必是周期函数
D.当f(x)是单调增函数时,F(x)必是单调增函数答案:B解析: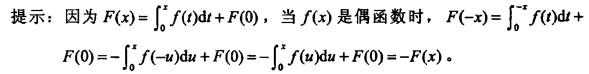
-
第18题:
设f(x)在(-a,a)(a>0)上连续,F(x)是f(x)的一个原函数,则当f(x)是奇函数时,下面结论正确的是()。
- A、F(x)是偶函数
- B、F(x)是奇函数
- C、F(x)可能是奇函数,也可能是偶函数
- D、F(x)是否为奇函数不能确定
正确答案:A -
第19题:
设f(x)在(-a,a)(a>0)上连续,F(x)是f(x)的一个原函数,则当f(x)是偶函数时,下面结论正确的是()。
- A、F(x)是偶函数
- B、F(x)是奇函数
- C、F(x)可能是奇函数,也可能是偶函数
- D、F(x)是否是偶函数不能确定
正确答案:D -
第20题:
单选题设函数f(x)在(-∞,+∞)上是偶函数,且在(0,+∞)内有f'(x)>0,f"(x)>0,则在(-∞,0)内必有()。Af'(x)>0,f"(x)>0
Bf'(x)<0,f"(x)>0
Cf'(x)>O,f"(x)<0
Df'(x)<0,f"(x)<0
正确答案: A解析: 暂无解析 -
第21题:
判断题设偶函数f(x)在区间(-1,1)内具有二阶导数,且f″(0)=f′(0)+1,则f(0)为f(x)的一个极小值。A对
B错
正确答案: 错解析: 暂无解析 -
第22题:
单选题设f(x)=-f(-x),x∈(-∞,+∞),且在(0,+∞)内f′(x)>0,f″(x)<0,则在(-∞,0)内( )。Af′(x)>0,f″(x)>0
Bf′(x)>0,f″(x)<0
Cf′(x)<0,f″(x)>0
Df′(x)<0,f″(x)<0
正确答案: D解析:
f(x)=-f(-x)⇔f(-x)=-f(x),则f(x)为奇函数。又f(x)可导,则f′(x)为偶函数,f″(x)存在且为奇函数,故在(-∞,0)内,f′(x)>0,f″(x)>0。 -
第23题:
单选题设f(x)在x=0处满足f′(0)=f″(0)=…=f(n)(0),f(n+1)(0)>0,则( )。A当n为偶数时,x=0是f(x)的极大值点
B当n为偶数时,x=0是f(x)的极小值点
C当n为奇数时,x=0是f(x)的极大值点
D当n为奇数时,x=0是f(x)的极小值点
正确答案: C解析:
此题可用举例法判断。当n=1时(即n为奇数),f′(0)=0,f″(0)>0。由f″(0)>0知f′(x)在x=0处单调增加。又f′(0)=0,x<0时f′(x)<0;x>0时f′(x)>0。因此f(x)在x=0点处取得极小值。
当n=2时(即n为偶数),f′(0)=f″(0)=0,f‴(0)>0。由f‴(0)>0知,f″(x)在x=0处单调增加。因f″(0)=0,故f′(x)在x=0附近先减小后增加。f′(0)=0,故f(x)在x=0点处单调。因此x=0既不是f(x)的极大值也不是它的极小值。综上所述D项正确。
