∫ln(1+x2)dx的值为( )。 A.xln(1+x2)+2(1-A.rC.tA.nx)+C. B.xln(1-x2)-2(x+A.rC.tA.nx)+C. C.xln(1+x2)-2(x-A.rC.tA.nx)+C. D.xln(1+x2)+2(x-A.rC.tA.nx)+C.

题目
∫ln(1+x2)dx的值为( )。

A.xln(1+x2)+2(1-A.rC.tA.nx)+C.
B.xln(1-x2)-2(x+A.rC.tA.nx)+C.
C.xln(1+x2)-2(x-A.rC.tA.nx)+C.
D.xln(1+x2)+2(x-A.rC.tA.nx)+C.
相似考题

1.函数y=ln(1＋x^2)在区间[－2,－1]上的最大值为()A、4B、0C、1D、ln5

2.若在[a,b]上用Ln(x)近似f(x)，则其截断误差为Rn(x)=f(x)-Ln(x)，也称为插值多项式的()A、余项B、插值公式C、插值多项式D、以上都不对

3.反应A→2B在温度T时的速率方程为dCA/dt=-k·CA，则此反应的半衰期为______。A、ln2/kB、2ln2/kC、k/ln2D、k·ln2

4.梁的上部钢筋第一排全部为4根通长筋,第二排为2根支座负筋,支座负筋长度为()。A、1/5Ln+锚固B、1/4Ln+锚固C、1/3Ln+锚固D、其他值

更多“∫ln(1+x2)dx的值为( )。 ”相关问题

  • 第1题：

    在主观Bayes方法中,专家给出的Ln和LS值,不能出现下两种情况()。

    A.LN<1,LS<1;LN<1,LS>1

    B.LN<1,LS>1;LN>1,LS<1

    C.LN<1,LS<1;LN>1,LS>1

    D.LN<1,LS>1;LN>1,LS>1


    答案：C

  • 第2题：

    微分方程(3+2y)xdx+(1+x2)dy=0 的通解为：
    A.1+x2=Cy B. (1+x2)(3+2y)=C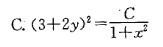
    D. (1+x2)2(3+2y)=C


    答案：B
    解析：
    提示:判断方程的类型为可分离变量方程，将方程分离变量得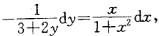两边
    积分计算。

  • 第3题：

    微分方程(3+2y)xdx+(1+x2)dy=0 的通解为：

    A.1+x2=Cy
    B. (1+x2)(3+2y)=C
    C.(3+2y)2=1/(1+x2)
    D. (1+x2)2(3+2y)=C

    答案：B
    解析：
    提示 判断方程的类型为可分离变量方程，将方程分离变量得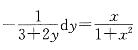dx，两边积分计算。

  • 第4题：

    若函数z=ln(xy)/y,则当x=e,y=e-1时，全微分dz等于（ ）。

    A. edx + dy B. e2dx-dy C. dx + e2dy D. edx+e2dy


    答案：C
    解析：
    正确答案是C。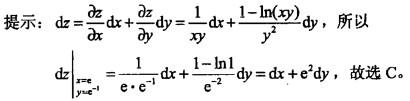

  • 第5题：

    某一装置如果需要发送采样值信号，必须要在相应LD的LN0中定义采样值数据集和（）节点。

    • A、Inputs
    • B、GSEControl
    • C、SampledValueControl
    • D、LN

    正确答案:C

  • 第6题：

    判断题
    当端支座为柱、剪力墙、框支梁或深梁时，梁端部上部支座筋取伸入跨内长度为Ln/3，Ln为相邻左右两跨中跨度较大一跨的跨度值。（）
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第7题：

    填空题
    设函数y＝y（x）由方程ln（x2＋y）＝x3y＋sinx确定，则（dy/dx）|x＝0＝____。

    正确答案： 1
    解析：
    ln（x2＋y）＝x3y＋sinx两边同时对x求导，得（2x＋y′）/（x2＋y）＝3x2y＋x3y′＋cosx，当x＝0时，y＝1，代入上式得y′（0）＝1。

  • 第8题：

    单选题
    设f（x）＝ex，f[g（x）]＝1－x2，则g（x）＝（　　）。
    A

    ln（1＋x2）

    B

    ex

    C

    －ln（1－x2）

    D

    ln（1－x2）


    正确答案： B
    解析：
    根据f[g（x）]＝eg（x）＝1－x2，可得g（x）＝ln（1－x2）。

  • 第9题：

    单选题
    当x＝（　　）时，函数y＝x·2x取得极小值。
    A

    ln2

    B

    －ln2

    C

    －1/ln2

    D

    1/ln2


    正确答案： A
    解析：
    由f′（x）＝2x（1＋xln2）＝0，得驻点为x＝－1/ln2，而f″（x）＝2x[2ln2＋x（ln2）2]，f″（－1/ln2）＞0。故函数y＝x·2x在点x＝－1/ln2处取得最小值。

  • 第10题：

    单选题
    设函数y＝y（x）由方程2xy＝x＋y所确定，则dy|x＝0＝（　　）。
    A

    （ln2－1）dx

    B

    （l－ln2）dx

    C

    （ln2－2）dx

    D

    ln2dx


    正确答案： C
    解析：
    2xy＝x＋y等式两边求微分，得2xyln2d（xy）＝dx＋dy，即2xyln2（xdy＋ydx）＝dx＋dy。当x＝0时，y＝1，代入上式得dy|x＝0＝（ln2－1）dx。

  • 第11题：

    单选题
    设y＝ln（cosx），则微分dy等于（　　）。[2012年真题]
    A

    dx/cosx

    B

    cotxdx

    C

    －tanxdx

    D

    －dx/（cosxsinx）


    正确答案： D
    解析：
    等式两边同时微分，得：dy＝f′（x）dx＝（－sinx）dx/cosx＝－tanxdx。

  • 第12题：

    单选题
    设函数y＝y（x）由方程2xy＝x＋y所确定，则dy|x＝0＝（　　）。
    A

    ln2－1

    B

    （ln2－1）dx

    C

    ln2＋1

    D

    （ln2＋1）dx


    正确答案： D
    解析：
    2xy＝x＋y等式两边求微分，得2xyln2d（xy）＝dx＋dy，即2xyln2（xdy＋ydx）＝dx＋dy。当x＝0时，y＝1，代入上式得dy|x＝0＝（ln2－1）dx。

  • 第13题：

    设曲线y=ln(1+x2)，M是曲线上的点，若曲线在M点的切线平行于已知直线y-x+1=0，则点M的坐标是( )。

    A.(-2，ln5)
    B.(-1，ln2)
    C.(1，ln2)
    D.(2，ln5)

    答案：C
    解析：
    在D选项中，利用函数在一点的导数的几何意义及平行的已知条件确定点的坐标

  • 第14题：

    函数y=ln(1+x2)的驻点为x=______．


    答案：
    解析：
    填0．

  • 第15题：

    微分方程(1+2y)xdx+(1+x2)dy的通解为:（c为任意常数）


    答案：B
    解析：
    提示 方程为一阶可分离变量方程，分离变量后求解。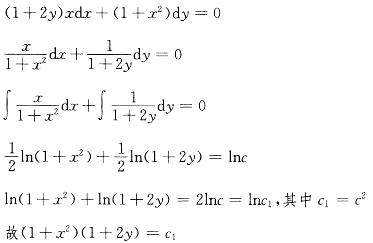

  • 第16题：

    在主观Bayes方法中，专家给出的Ln和LS值，不能出现下两种情况（）。 Ⅰ.LN<1，LS<1 Ⅱ.LN<1，LS>1 Ⅲ.LN>1，LS<1 Ⅳ.LN>1，LS>1

    • A、Ⅰ，Ⅱ
    • B、Ⅱ，Ⅲ
    • C、Ⅰ，Ⅳ
    • D、Ⅱ，Ⅳ

    正确答案:C

  • 第17题：

    设x是值大于零的实型变量，计算PASCAL中x8的表达式为（）。

    • A、ln（8*exp（x））
    • B、exp（8*ln（x））
    • C、x^8
    • D、sqr（sqr（sqr（x）））*x

    正确答案:B

  • 第18题：

    单选题
    设I＝∫[（ex－1）/（ex＋1）]dx，则I＝（　　）。
    A

    ln（1＋ex）＋C

    B

    2ln（1＋ex）－x＋C

    C

    x－2ln（1＋ex）＋C

    D

    ln（ex－1）＋C


    正确答案： A
    解析：
    由于[－x＋2ln（1＋ex）]′＝－1＋[2ex/（1＋ex）]＝（ex－1）/（1＋ex），故B项正确。

  • 第19题：

    单选题
    在主观Bayes方法中，专家给出的Ln和LS值，不能出现下两种情况（）。 Ⅰ.LN1 Ⅲ.LN>1，LS1，LS>1
    A

    Ⅰ，Ⅱ

    B

    Ⅱ，Ⅲ

    C

    Ⅰ，Ⅳ

    D

    Ⅱ，Ⅳ


    正确答案： B
    解析： 暂无解析

  • 第20题：

    单选题
    初值问题y″＝e2y＋ey，y（0）＝0，y′（0）＝2的解为（　　）。
    A

    y－ln（1＋ey）＝x＋ln2

    B

    y＋ln（1＋ey）＝x－ln2

    C

    y＋ln（1＋ey）＝x＋ln2

    D

    y－ln（1＋ey）＝x－ln2


    正确答案： C
    解析：
    将微分方程y″＝e2y＋ey两边乘以2y′，得2y′y″＝（e2y＋ey）2y′，d（y′2）＝2（e2y＋ey）dy。两边积分得y′2＝2e2y＋ey＋C。将y（0）＝0，y′（0）＝2代入上式，得C＝1，故y′＝1＋ey，则有dy/（1＋ey）＝dx。积分可得y－ln（1＋ey）＝x＋C1，将y（0）＝0代入上式，得C1＝－ln2。故方程的解为y－ln（1＋ey）＝x－ln2

  • 第21题：

    填空题
    设y＝f[（2x－1）/（x＋1）]，f′（x）＝ln（x1/3），则dy/dx____。

    正确答案： ln[(2x-1)/(x+1)]/(x+1)2
    解析：
    令u＝（2x－1）/（x＋1），则u′（x）＝3/（x＋1）2。dy/dx＝f′（u）·u′（x）＝ln（u1/3）·3/（x＋1）2＝ln[（2x－1）/（x＋1）]/（x＋1）2。

  • 第22题：

    单选题
    若函数f（x）的反函数f－1（x）＝1＋x2（x＜0），则f（2）的值为（　　）．
    A

    1

    B

    －1

    C

    1或－1

    D

    5


    正确答案： A
    解析：
    设f（2）＝x，贝f－1（x）＝2，即1＋x2＝2（x＜0），得x＝－1．

  • 第23题：

    单选题
    当x＝（　　）时，函数y＝x·2x取得极小值。
    A

    1/ln2

    B

    －ln2

    C

    ln2

    D

    －1/ln2


    正确答案： A
    解析：
    由f′（x）＝2x（1＋xln2）＝0，得驻点为x＝－1/ln2，而f″（x）＝2x[2ln2＋x（ln2）2]，f″（－1/ln2）＞0。故函数y＝x·2x在点x＝－1/ln2处取得最小值。

相关内容