设y=f(x)是(a, b)内的可导函数，X,X+ΔX是(a, b)内的任意两点，则： (A) Δy= f‘ (x)Ax (B)在x，x+Ax之间恰好有一点ξ，使Δy=f'(ξ)Ax (C)在x, x+Ax之间至少有一点ξ，使Δy=f'(ξ)Ax (D)对于x，x+ax之间任意一点ξ，使Δy=f'(ξ)Ax

题目

设y=f(x)是(a, b)内的可导函数，X,X+ΔX是(a, b)内的任意两点，则：
(A) Δy= f‘ (x)Ax
(B)在x，x+Ax之间恰好有一点ξ，使Δy=f'(ξ)Ax
(C)在x, x+Ax之间至少有一点ξ，使Δy=f'(ξ)Ax
(D)对于x，x+ax之间任意一点ξ，使Δy=f'(ξ)Ax

相似考题

1.设X、Y的联合分布函数是F(x,y),则F(＋∞,y)等于:()A、0;B、1;C、Y的分布函数;D、Y的密度函数。

2.设f（x）、f'（x）为已知的连续函数，则微分方程y'+ f'（x）y = f（x）f'（x）的通解是：

3.设y=f(x)是(a,b)内的可导函数，x和x+Δx是(a,b)内的任意两点，则: A. Δy=f' (x)Δx B.在x，x+Δx之间恰好有一点ξ，使Δy=f' (ξ)Δx C.在x，x+Δx之间至少有一点ξ，使Δy=f' (ξ)Δx D.在x，x+Δx之间任意一点ξ，使Δy=f' (ξ)Δx

4.设函数y=f(x)在(0，+∞)内有界且可导，则( )。A. B. C. D.

更多“设y=f(x)是(a, b)内的可导函数，X,X+ΔX是(a, b)内的任意两点，则： ”相关问题

第1题：

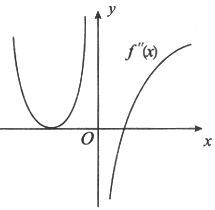
设函数f(x)在(-∞，+∞)内连续，其二阶导函数f"(x)的图形如图所示，则曲线y=f(x)的拐点个数为
　　

A.A0
B.1
C.2
D.3

答案：C
解析：
由如图知f"(x1)=f"(x2)=0，f"(0)不存在，其余点上二阶导数f"(x)存在且非零，则曲线y=f(x)最多三个拐点，但在x=x1的两侧二阶导数不变号.因此，不是拐点，而在x=0和x=x2的两侧二阶导数变号，则曲线y=f(x)有两个拐点，故应选(C).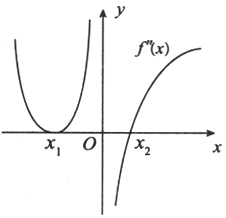　　
第2题：

设f(x)是周期为4的可导奇函数，且f'(x)=2(x-1)，x∈［0，2］，则f(7)=________.

答案：1、1.
解析：
由f'(x)=2(x-1)，x∈［0，2］知，f(x)=(x-1)^2+C.又f(x)为奇函数，则f(0)=0,C=-1.f(x)=(x-1)^2-1.由于f(x)以4为周期，则f(7)=f［8+(-1)］=f(-1)=-f(1)=1.
第3题：

设y=f（x）是（a，b）内的可导函数，x，x+△x是（a，b）内的任意两点，则：

A. △y=f’（x）△x
B.在x，x+△x之间恰好有一点ξ，使△y=f’（ξ）△x
C.在x，x+△x之间至少存在一点ξ，使△y=f’（ξ）△x
D.在x，x+△x之间的任意一点ξ，使△y=f’（ξ）△x

答案：C
解析：
第4题：

填空题
设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。

正确答案： -1/7
解析：
由方程y＝f（x²＋y²）＋f（x＋y）。两边对x求导得y_x′＝f′（x²＋y²）（2x＋2y·y_x′）＋f′（x＋y）（1＋y_x′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，，故y′|_x_＝₀＝f′（4）·4y′|_x_＝₀＋f′（2）（1＋y′|_x_＝₀），y′|_x_＝₀＝4y′|_x_＝₀＋（1＋y′|_x_＝₀）/2，解得y′|_x_＝₀＝－1/7。
第5题：

单选题
设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。
A
1/5
B
1/7
C
－1/7
D
－1/5

正确答案： B
解析：
由方程y＝f（x²＋y²）＋f（x＋y）。两边对x求导得y_x′＝f′（x²＋y²）（2x＋2y·y_x′）＋f′（x＋y）（1＋y_x′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，故y′|_x_＝₀＝f′（4）·4y′|_x_＝₀＋f′（2）（1＋y′|_x_＝₀），y′|_x_＝₀＝4y′|_x_＝₀＋（1＋y′|_x_＝₀）/2，解得y′|_x_＝₀＝－1/7。
第6题：

单选题
（2009）设y=f（x）是（a，b）内的可导函数，x+△x是（a，b）内的任意两点，则：（）
A
△y=f′（x）△x
B
在x，x+△x之间恰好有一点ξ，使△y=f′（ξ）△x
C
在x，x+△x之间至少有一点ξ，使△y=f′（ξ）△x
D
在x，x+△x之间任意一点ξ，使△y=f′（ξ）△x

正确答案： C
解析：暂无解析
第7题：

单选题
若函数f（x）在区间（a，b）内可导，x1和x2是区间（a，b）内任意两点（x1＜x2），则至少存在一点ξ，使（　　）
A
f（b）－f（a）＝f′（ξ）（b－a）（a＜ξ＜b）
B
f（b）－f（x₁）＝f′（ξ）（b－x₁）（x₁＜ξ＜b）
C
f（x₂）－f（x₁）＝f′（ξ）（x₂－x₁）（x₁＜ξ＜x₂）
D
f（x₂）－f（a）＝f′（ξ）（x₂－a）（a＜ξ＜x₂）

正确答案： C
解析：
考查拉格朗日中值定理的应用。
值得注意的是，当函数f（x）在[a，b]上连续且在（a，b）内可导时，才可在[a，b]上对函数f（x）应用拉格朗日中值定理。
由于题中没有说明函数f（x）在[a，b]上连续，因此有可能f（x）在x＝a或x＝b上没有定义，选项中涉及f（a）、f（b）的均为错误选项。
第8题：

填空题
设f（u，v）是二元可微函数，z＝f（y/x，x/y），则x∂z/∂x－y∂z/∂y＝____。

正确答案： 2(-yf₁′/x+xf₂′/y)
解析：
设f₁′为函数f（u，v）对第一中间变量的偏导，f₂′为函数f（u，v）对第二中间变量的偏导，则∂z/∂x＝f₁′·（－y/x²）＋f₂′·（1/y），∂z/∂y＝f₁′·（1/x）＋f₂′·（－x/y²），x∂z/∂x－y∂z/∂y＝2（－yf₁′/x＋xf₂′/y）。
第9题：

填空题
设f（x）是可导函数，且f′（x）＝sin2[sin（x＋1）]，f（0）＝4，f（x）的反函数是x＝φ（y），则φ′（4）＝____。

正确答案： 1/sin²(sin1)
解析：
φ′（4）＝1/f′（0）＝1/sin²（sin1）。
第10题：

填空题
设函数z＝z（x，y）由方程F（x－az，y－bz）＝0所给出，其中F（u，v）任意可微，则a∂z/∂x＋（b∂z/∂y）＝____。

正确答案： 1
解析：
根据偏导数的求解方法可知∂z/∂x＝－F_x′/F_z′＝－F₁′/（―aF₁′―bF₂′），∂z/∂y＝－F_y′/F_z′＝－F₂′/（―aF₁′―bF₂′），故a∂z/∂x＋（b∂z/∂y）＝－（aF₁′＋bF₂′）/（―aF₁′―bF₂′）＝1。
第11题：

单选题
设函数f（x）在区间[1，＋∞）内二阶可导，且满足条件f（1）＝f′（1）＝0，x＞1时f″（x）＜0，则g（x）＝f（x）/x在（1，＋∞）内（　　）。
A
曲线是向上凹的
B
曲线是向上凸的
C
单调减少
D
单调增加

正确答案： C
解析：
判断函数的单调性及凹凸性，需求出其导函数和二阶导数，并判断其正负号。g′（x）＝[xf′（x）－f（x）]/x²，构造函数F（x）＝xf′（x）－f（x），F′（x）＝xf″（x）＜0（题中已给出f″（x）＜0），故F（x）单调减少。则F（x）＜F（1）＝0，故g′（x）＜0，即g（x）在（1，＋∞）内单调减少。
第12题：

设函数，(u)可导，z=f(sin y-sin x)+xy，则=__________.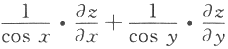

答案：
解析：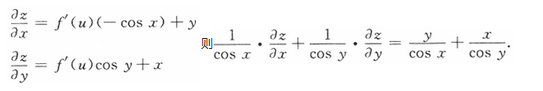
第13题：

下列命题中，正确的是( ).

A.单调函数的导函数必定为单调函数
B.设f´(x)为单调函数，则f(x)也为单调函数
C.设f(x)在(a，b)内只有一个驻点xo，则此xo必为f(x)的极值点
D.设f(x)在(a，b)内可导且只有一个极值点xo，f´(xo)=0

答案：D
解析：
可导函数的极值点必定是函数的驻点，故选D.
第14题：

设f（x）和g（x）在（-∞，+∞）内可导，且f（x）＜g（x），则必有（）《》（）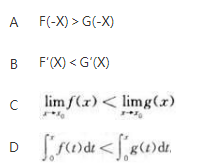

答案：C
解析：
第15题：

填空题
设函数f（x）在x＝2的某邻域内可导，且f′（x）＝ef（x），f（2）＝1，则f‴（2）＝____。

正确答案： 2e³
解析：
因f′（x）＝e^f^（^x^）方程两边对x求导，得f″（x）＝e^f^（^x^）·f′（x）＝e^f^（^x^）·e^f^（^x^）＝e^2f^（^x^），两边再对x求导，得f‴（x）＝e^2f^（^x^）·2f′（x）＝2e^2f^（^x^）·e^f^（^x^）＝2e^3f^（^x^）。又f（2）＝1，则f‴（2）＝2e^3f^（²^）＝2e³。
第16题：

填空题
设函数z＝z（x，y）由方程z＝e2x－3z＋2y确定，则3∂z/∂x＋∂z/∂y＝____。

正确答案： 2
解析：
方程两边同时对x求偏导，则∂z/∂x＝e^2x^－^3z（2－3∂z/∂x），可得∂z/∂x＝2e^2x^－^3z/（1＋3e^2x^－^3z）。同理∂z/∂y＝e^2x^－^3z（－3∂z/∂y）＋2，可得∂z/∂y＝2/（1＋3e^2x^－^3z），所以3∂z/∂x＋∂z/∂y＝6e^2x^－^3z/（1＋3e^2x^－^3z）＋2/（1＋3e^2x^－^3z）＝2（1＋3e^2x^－^3z）/（1＋3e^2x^－^3z）＝2。
第17题：

单选题
设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（　　）。
A
1
B
－1
C
1/7
D
－1/7

正确答案： B
解析：
由方程y＝f（x²＋y²）＋f（x＋y）。两边对x求导得y_x′＝f′（x²＋y²）（2x＋2y·y_x′）＋f′（x＋y）（1＋y_x′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，故y′|_x_＝0＝f′（4）·4y′|_x_＝0＋f′（2）（1＋y′|_x_＝0），y′|_x_＝0＝4y′|_x_＝0＋（1＋y′|_x_＝0）/2，解得y′|_x_＝0＝－1/7。
第18题：

单选题
设函数z＝z（x，y）由方程F（x－az，y－bz）＝0所给出，其中F（u，v）任意可微，则a∂z/∂x＋（b∂z/∂y）＝（　　）。
A
1
B
2
C
3
D
4

正确答案： A
解析：
根据偏导数的求解方法可知∂z/∂x＝－F_x′/F_z′＝－F₁′/（―aF₁′―bF₂′），∂z/∂y＝－F_y′/F_z′＝－F₂′/（―aF₁′―bF₂′），故a∂z/∂x＋（b∂z/∂y）＝－（aF₁′＋bF₂′）/（―aF₁′―bF₂′）＝1。
第19题：

问答题
设f（x）在（a，b）内二阶可导，且f″（x）≥0，证明：对于（a，b）内任意两点x1、x2及0≤t≤1，有f[（1－t）x1＋tx2]≤（1－t）f（x1）＋tf（x2）。

正确答案：
由于不等式中含有f[(1-t)x₁+tx₂]、f(x₁)、f(x₂),则应在x₀=(1-t)x₁+tx₂处展开泰勒式,即f(x)=f(x₀)+f′(x₀)(x-x₀)+f″(ξ)(x-x₀)²/(2!),ξ介于x和x₀之间。
又f″(x)≥0,则f″(ξ)≥0。故f(x)≥f(x₀)+f′(x₀)(x-x₀)。则
f(x₁)≥f(x₀)+f′(x₀)(x₁-x₀)①
f(x₂)≥f(x₀)+f′(x₀)(x₂-x₀)②
①(1-t)+②t,得(1-t)f(x₁)+tf(x₂)≥f(x₀)+f′(x₀)[(1-t)x₁+tx₂-x₀]=f(x₀),即(1-t)f(x₁)+tf(x₂)≥f[(1-t)x₁+tx₂]。
解析：暂无解析
第20题：

单选题
设f（x）在（－∞，＋∞）内可导，且对任意x2＞x1，都有f（x2）＞f（x1），则正确的结论是（　　）。
A
对任意x，f′（x）＞0
B
对任意x，f′（x）≤0
C
函数－f（－x）单调增加
D
函数f（－x）单调增加

正确答案： A
解析：
令F（x）＝－f（－x），由题知x₂＞x₁，则－x₂＜－x₁，则有f（－x₂）＜f（－x₁），即－f（－x₂）＞－f（－x₁），即F（x₂）＞F（x₁）单调增加，C正确。取f（x）＝x³，可排除A项。取f（x）＝x，可排除B、D项。
第21题：

单选题
设函数f（x）在x＝2的某邻域内可导，且f′（x）＝ef（x），f（2）＝1，则f‴（2）＝（　　）。
A
e²
B
2e²
C
e³
D
2e³

正确答案： B
解析：
因f′（x）＝e^f^（x^）方程两边对x求导，得f″（x）＝e^f^（x^）·f′（x）＝e^f^（x^）·e^f^（x^）＝e^2f^（x^），两边再对x求导，得f‴（x）＝e^2f^（x^）·2f′（x）＝2e^2f^（x^）·e^f^（x^）＝2e^3f^（x^）。又f（2）＝1，则f‴（2）＝2e^3f^（2^）＝2e³。
第22题：

单选题
设函数f（u）可导，y＝f（x2），当自变量x在x＝－1处取得增量Δx＝－0.1时，相应的函数的增量Δy的线性主部为0.1，则f′（1）＝（　　）。
A
－1
B
0.1
C
1
D
0.5

正确答案： B
解析：
由dy＝f′（x²）dx²＝2xf′（x²）dx，则0.1＝－2f′（1）（－0.1），即f′（1）＝0.5。

设y=f(x)是(a, b)内的可导函数，X,X+ΔX是(a, b)内的任意两点，则： (A) Δy= f‘ (x)Ax (B)在x，x+Ax之间恰好有一点ξ，使Δy=f'(ξ)Ax (C)在x, x+Ax之间至少有一点ξ，使Δy=f'(ξ)Ax (D)对于x，x+ax之间任意一点ξ，使Δy=f'(ξ)Ax

题目

相似考题

更多“设y=f(x)是(a, b)内的可导函数，X,X+ΔX是(a, b)内的任意两点，则： ”相关问题

相关内容