设函数y=f(x)在(0，+∞)内有界且可导，则( )。A. B. C. D.
题目
设函数y=f(x)在(0，+∞)内有界且可导，则( )。
A.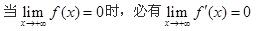
B.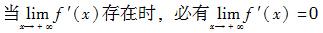
C.
D.
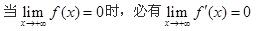
B.
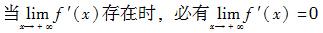
C.
D.
相似考题
更多“设函数y=f(x)在(0，+∞)内有界且可导，则( )。”相关问题
-
第1题：
设函数f(x)在(-∞，+∞)内连续，其二阶导函数f"(x)的图形如图所示，则曲线y=f(x)的拐点个数为
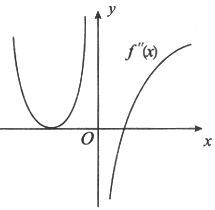A.A0
B.1
C.2
D.3答案：C解析：由如图知f"(x1)=f"(x2)=0，f"(0)不存在，其余点上二阶导数f"(x)存在且非零，则曲线y=f(x)最多三个拐点，但在x=x1的两侧二阶导数不变号.因此，不是拐点，而在x=0和x=x2的两侧二阶导数变号，则曲线y=f(x)有两个拐点，故应选(C).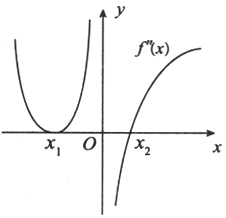
-
第2题：
设函数，(u)可导，z=f(sin y-sin x)+xy，则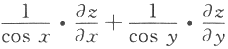
=__________.答案：解析：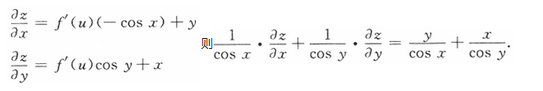
-
第3题：
(Ⅰ)证明拉格朗日中值定理：若函数f(x)在［a，b］上连续，在(a，b)内可导，则存在ξ∈(a，b)，使得f(b)-f(a)=f'(ξ)(b-a)；(Ⅱ)证明：若函数f(x)在x=0处连续，在(0，δ)(δ>0)内可导，且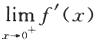
=A，则
存在，且.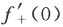
答案：解析：
-
第4题：
下列命题中，正确的是( ).A.单调函数的导函数必定为单调函数
B.设f´(x)为单调函数，则f(x)也为单调函数
C.设f(x)在(a，b)内只有一个驻点xo，则此xo必为f(x)的极值点
D.设f(x)在(a，b)内可导且只有一个极值点xo，f´(xo)=0答案：D解析：可导函数的极值点必定是函数的驻点，故选D. -
第5题：
设
其中g(x)是有界函数，则f(x)在x=0点( )。A、极限不存在
B、极限存在但不连续
C、连续、但不可导
D、可导答案：D解析：
-
第6题：
设f(x)是R上的可导函数，且f(x)>0。若f′(x)-3x---2f(x)=0，且f(0)=1，求f(x)。答案：解析：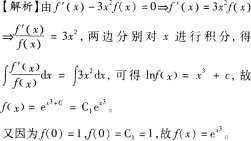
-
第7题：
设函数在（a，b）内连续，则在（a，b）内（）。
- A、f（x）必有界
- B、f（x）必可导
- C、f（x）必存在原函数
- D、D.必存在一点ξ∈（a，，使f（ξ）=0
正确答案:C -
第8题：
填空题设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝____。正确答案： -1/7解析：
由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。 -
第9题：
填空题设函数f（x）在x＝2的某邻域内可导，且f′（x）＝ef（x），f（2）＝1，则f‴（2）＝____。正确答案： 2e3解析：
因f′（x）＝ef（x）方程两边对x求导，得f″（x）＝ef（x）·f′（x）＝ef（x）·ef（x）＝e2f（x），两边再对x求导，得f‴（x）＝e2f（x）·2f′（x）＝2e2f（x）·ef（x）＝2e3f（x）。又f（2）＝1，则f‴（2）＝2e3f（2）＝2e3。 -
第10题：
单选题设函数f(x)=丨x丨，则函数在点x=0处（）A连续且可导
B连续且可微
C连续不可导
D不可连续不可微
正确答案： C解析： 暂无解析 -
第11题：
填空题设f（x）是可导函数，且f′（x）＝sin2[sin（x＋1）]，f（0）＝4，f（x）的反函数是x＝φ（y），则φ′（4）＝____。正确答案： 1/sin2(sin1)解析：
φ′（4）＝1/f′（0）＝1/sin2（sin1）。 -
第12题：
单选题设函数f（x）在区间[1，＋∞）内二阶可导，且满足条件f（1）＝f′（1）＝0，x＞1时f″（x）＜0，则g（x）＝f（x）/x在（1，＋∞）内（ ）。A曲线是向上凹的
B曲线是向上凸的
C单调减少
D单调增加
正确答案： C解析：
判断函数的单调性及凹凸性，需求出其导函数和二阶导数，并判断其正负号。g′（x）＝[xf′（x）－f（x）]/x2，构造函数F（x）＝xf′（x）－f（x），F′（x）＝xf″（x）＜0（题中已给出f″（x）＜0），故F（x）单调减少。则F（x）＜F（1）＝0，故g′（x）＜0，即g（x）在（1，＋∞）内单调减少。 -
第13题：
设函数z=z(x，y)由方程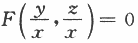
确定，其中F为可微函数，且F'2≠0，则
=A.Ax
B.z
C.-x
D.-z答案：B解析：
-
第14题：
设f(x)是周期为4的可导奇函数，且f'(x)=2(x-1)，x∈［0，2］，则f(7)=________.答案：1、1.解析：由f'(x)=2(x-1)，x∈［0，2］知，f(x)=(x-1)^2+C.又f(x)为奇函数，则f(0)=0,C=-1.f(x)=(x-1)^2-1.由于f(x)以4为周期，则f(7)=f［8+(-1)］=f(-1)=-f(1)=1. -
第15题：
设函数f(x)具有2阶连续导数，若曲线y=f(x)过点(0，0)且与曲线y=^x在点(1，2)处相切，则
=________.答案：1、2(ln2-1)解析：
-
第16题：
函数y=f（x）在（a，6）内二阶可导，且f′（x）＞0，f″（x）＜0，则曲线y=f（x）在（a，6）内（ ）.《》（ ）A.单调增加且为凹
B.单调增加且为凸
C.单调减少且为凹
D.单调减少且为凸答案：B解析：本题考查的知识点为利用一阶导数符号判定函数的单调性和利用二阶导数符号判定曲线的凹凸性.由于在（a，6）内，f′（x）＞0，可知f（x）在（a，b）内单调增加，又由于，f″（x）＜0，可知曲线y=f（x）在（a，b）内为凸，可知应选B. -
第17题：
若函数f(x)在[0，1]上黎曼可积，则f(x)在[0，1]上（ ）。A.连续
B.单调
C.可导
D.有界答案：D解析：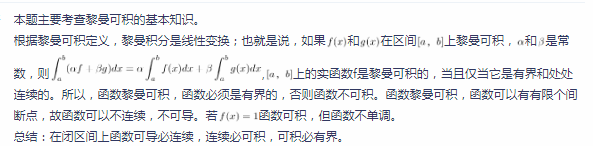
-
第18题：
设y=f(x)可导，点a0=2为f(x)的极小值点，且f(2)=3，则曲线y=f(x)在点(2，3)处的切线方程为______．答案：解析：由于y=f(x)可导，点x0=2为f(x)的极小值点，由极值的必要条件可知f′(2)=0．曲线y=fx)在点(2，3)处的切线方程为y-3=f′(2)(x-2)=0，即y=3为所求切线方程． -
第19题：
设函数f(x)=丨x丨，则函数在点x=0处（）
- A、连续且可导
- B、连续且可微
- C、连续不可导
- D、不可连续不可微
正确答案:C -
第20题：
单选题设函数在（a，b）内连续，则在（a，b）内（）。Af（x）必有界
Bf（x）必可导
Cf（x）必存在原函数
DD.必存在一点ξ∈（a，，使f（ξ）=0
正确答案： A解析： 暂无解析 -
第21题：
单选题设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（ ）。A1/5
B1/7
C－1/7
D－1/5
正确答案： B解析：
由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。 -
第22题：
单选题设函数y＝y（x）由方程y＝f（x2＋y2）＋f（x＋y）所确定，且y（0）＝2，其中f是可导函数，f′（2）＝1/2，f′（4）＝1，则dy/dx|x＝0＝（ ）。A1
B－1
C1/7
D－1/7
正确答案： B解析：
由方程y＝f（x2＋y2）＋f（x＋y）。两边对x求导得yx′＝f′（x2＋y2）（2x＋2y·yx′）＋f′（x＋y）（1＋yx′）。
又y（0）＝2，f′（2）＝1/2，f′（4）＝1，故y′|x＝0＝f′（4）·4y′|x＝0＋f′（2）（1＋y′|x＝0），y′|x＝0＝4y′|x＝0＋（1＋y′|x＝0）/2，解得y′|x＝0＝－1/7。 -
第23题：
单选题设f（x）在（－∞，＋∞）内可导，且对任意x2＞x1，都有f（x2）＞f（x1），则正确的结论是（ ）。A对任意x，f′（x）＞0
B对任意x，f′（x）≤0
C函数－f（－x）单调增加
D函数f（－x）单调增加
正确答案： A解析：
令F（x）＝－f（－x），由题知x2＞x1，则－x2＜－x1，则有f（－x2）＜f（－x1），即－f（－x2）＞－f（－x1），即F（x2）＞F（x1）单调增加，C正确。取f（x）＝x3，可排除A项。取f（x）＝x，可排除B、D项。