设A为n阶矩阵，则A以零为其特征值是A为奇异矩阵(即 A =0)的: A.充分非必要条件 B.必要非充分条件 C.既非充分也非必要条件 D.充分必要条件
题目
设A为n阶矩阵，则A以零为其特征值是A为奇异矩阵(即 A =0)的:
A.充分非必要条件
B.必要非充分条件
C.既非充分也非必要条件
D.充分必要条件
A.充分非必要条件
B.必要非充分条件
C.既非充分也非必要条件
D.充分必要条件
相似考题
更多“设A为n阶矩阵，则A以零为其特征值是A为奇异矩阵(即 A =0)的: ”相关问题
-
第1题：
设A为n阶矩阵,k为常数,则(kA)+等于().
答案：C解析：
-
第2题：
设三阶矩阵A的特征值为λ1=1,λ2=0,λ3=1,则下列结论不正确的是().A.矩阵A不可逆
B.矩阵A的迹为零
C.特征值-1,1对应的特征向量正交
D.方程组AX=0的基础解系含有一个线性无关的解向量答案：C解析：由λ1=-1，λ2=0，λ3=1得|A|=0，则r(A)小于3，即A不可逆，(A)正确；又λ1+λ2+λ3=tr(A)=0，所以(B)正确；因为A的三个特征值都为单值，所以A的非零特征值的个数与矩阵A的秩相等，即r(A)=2，从而AX=0的基础解系仅含有一个线性无关的解向量，(D)是正确的；(C)不对，因为只有实对称矩阵的不同特征值对应的特征向量正交，一般矩阵不一定有此性质，所以选(C). -
第3题：
设A为m×n矩阵，C是n阶可逆矩阵，矩阵A的秩为r1，矩阵B=AC的秩为r，则
答案：C解析： -
第4题：
已知n阶可逆矩阵A的特征值为λ0，则矩阵(2A)-1的特征值是：
答案：C解析：
-
第5题：
设A为n阶非奇异矩阵，α为n维列向量，b为常数.记分块矩阵
.其中A*是矩阵A的伴随矩阵，E是n阶单位矩阵. （1）计算并化简PQ； （2）证明：矩阵Q可逆的充分必要条件是.
答案：解析：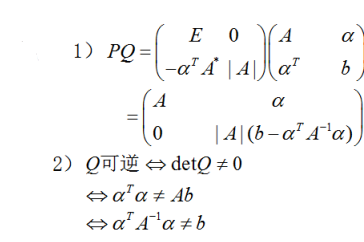
-
第6题：
设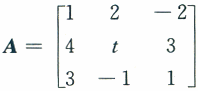
，B为三阶非零矩阵，且AB=0，则t=________.答案：1、-3.解析：由AB=0，对B按列分块有AB=A(β1，β2，β3)=(Aβ1，Aβ2，Aβ3)=(0,0,0)，即β1，β2，β3是齐次方程组Ax=0的解，又因B≠0，故Ax=0有非零解，那么
若熟悉公式：AB=0，则r(A)+r(B)≤n.可知r(A)<3.亦可求出t=-3.
【评注】对于AB=O要有B的每个列向量都是齐次方程组Ax=0的构思，还要有秩r(A)+r(B)≤n的知识. -
第7题：
设A为m×n阶实矩阵,且r(A)=n.证明：A^TA的特征值全大于零.答案：解析：
-
第8题：
设a为N阶可逆矩阵，则（ ）.《》（ ）
答案：C解析： -
第9题：
填空题设n维向量α(→)＝（a，0，…，0，a）T，a＜0，E为n阶单位矩阵，矩阵A＝E－α(→)α(→)T，B＝E＋α(→)α(→)T/a，且B为A的逆矩阵，则a＝____。正确答案： -1解析：
由矩阵B是矩阵A的逆矩阵，所以有AB＝E。从而（E－ααT）（E＋ααT/a）＝E－ααT＋ααT/a－α（αTα）αT/a＝E，即ααT（1/a－1－2a2/a）＝0。
由于ααT≠0，故1/a－1－2a2/a＝0，又因a＜0，可得a＝－1。 -
第10题：
填空题设A为n阶方阵，若对任意n×m（m≥n）矩阵B都有AB=0，则A=____.正确答案： 0解析：
取基本单位向量组为ε1，ε2，…εn
当m=n时，由对任意B都有AB=0，则对B=（ε1，ε2，…εn）=En也成立，即AE=0，故A=0．
当m>n时，取B=（ε1，ε2，…εn，B1）=（En，B1），则由AB=A（En，B1）=0，知AEn=0，故A=0． -
第11题：
单选题设n维向量α(→)＝（a，0，…，0，a）T，a＜0，E为n阶单位矩阵，矩阵A＝E－α(→)α(→)T，B＝E＋α(→)α(→)T/a，且B为A的逆矩阵，则a＝（ ）。A4
B2
C－1
D1
正确答案： B解析：
由矩阵B是矩阵A的逆矩阵，所以有AB＝E。从而（E－ααT）（E＋ααT/a）＝E－ααT＋ααT/a－α（αTα）αT/a＝E，即ααT（1/a－1－2a2/a）＝0。
由于ααT≠0，故1/a－1－2a2/a＝0，又因a＜0，可得a＝－1。 -
第12题：
填空题设n阶矩阵A的各行元素之和均为零，且A的秩为n－1，则线性方程组AX(→)＝0(→)的通解为____。正确答案： X=k(1,1,…,1)T解析：
由r（A）＝n－1，知方程组AX＝0的基础解系只含有n－（n－1）＝1个解向量。又矩阵A的各行元素之和为0，知（1，1，…，1）T，为AX＝0的非零解，则方程组AX＝0的通解为X＝k（1，1，…，1）T。 -
第13题：
设A,B为n阶可逆矩阵,则().
答案：D解析：因为A，B都是可逆矩阵，所以A，B等价，即存在可逆矩阵P，Q，使得PAQ=B，选(D). -
第14题：
设n阶矩阵A与对角矩阵相似,则().A.A的n个特征值都是单值
B.A是可逆矩阵
C.A存在n个线性无关的特征向量
D.A一定为n阶实对称矩阵答案：C解析：矩阵A与对角阵相似的充分必要条件是其有n个线性无关的特征向量，A有n个单特征值只是其可对角化的充分而非必要条件，同样A是实对称阵也是其可对角化的充分而非必要条件，A可逆既非其可对角化的充分条件，也非其可对角化的必要条件，选(C). -
第15题：
设A是n阶矩阵，且Ak=O(k为正整数)，则( )。A.A一定是零矩阵
B.A有不为0的特征值
C.A的特征值全为0
D.A有n个线性无关的特征向量答案：C解析：
-
第16题：
设A为n阶矩阵,且｜A｜=0,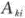
≠0,则AX=0的通解为_______.答案：解析：
-
第17题：
设A、B、C为同阶矩阵，且C为非奇异矩阵，满足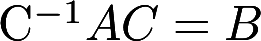
，求证：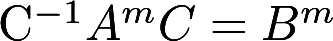
答案：解析：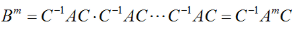
-
第18题：
设A为n阶矩阵,A的各行元素之和为0且r(A)=n-1,则方程组AX=0的通解为_______.答案：解析：
-
第19题：
设A为二阶矩阵，α1，α2为线性无关的二维列向量，Aα1=0，Aα2=2α1+α2，则A的非零特征值为________.答案：1、1.解析：
-
第20题：
设A为n阶方阵，A*是A的伴随矩阵，则||A|A*|等于（ ）.
答案：D解析：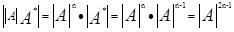
-
第21题：
填空题设，B为三阶非零矩阵，且AB＝0，则t＝____。正确答案： -3解析：
由B是三阶非零矩阵，且AB＝0，知B的列向量是方程组AB＝0的解且为非零解，故|A|＝0，解得t＝－3。 -
第22题：
单选题设n维向量α(→)＝（a，0，…，0，a）T，a＜0，E为n阶单位矩阵，矩阵A＝E－α(→)α(→)T，B＝E＋α(→)α(→)T/a，且B为A的逆矩阵，则a＝（ ）。A－2
B－1
C0
D1
正确答案： A解析：
由矩阵B是矩阵A的逆矩阵，所以有AB＝E。从而（E－ααT）（E＋ααT/a）＝E－ααT＋ααT/a－α（αTα）αT/a＝E，即ααT（1/a－1－2a2/a）＝0。
由于ααT≠0，故1/a－1－2a2/a＝0，又因a＜0，可得a＝－1。 -
第23题：
单选题已知n阶可逆矩阵A的特征值为λ0，则矩阵（2A）－1的特征值是（ ）。[2012年真题]A2/λ0
Bλ0/2
C1/（2λ0）
D2λ0
正确答案： D解析：
由矩阵特征值的性质，2A的特征值为2λ0，因此（2A）－1的特征值为1/（2λ0）。