微分方程y,,-4y=4的通解是：（c1,c2为任意常数）
题目
微分方程y,,-4y=4的通解是：（c1,c2为任意常数）
相似考题
参考答案和解析
答案：B
解析：
先求对应的齐次方程的通解，特征方程为r2 -4 = 0,特征根R 1,2 =±2，则齐次方程的通解
又特解为-1，则方程的通解为
点评：非齐次方程的通解由对应的齐次方程的通解和特解组成。
又特解为-1，则方程的通解为
点评：非齐次方程的通解由对应的齐次方程的通解和特解组成。
更多“微分方程y,,-4y=4的通解是：（c1,c2为任意常数） ”相关问题
-
第1题：
微分方程y"-4y=6的通解是(c1，c2为任意常数)：A. c1e2x-c2e-2x+1
B. c1e2x+c2e-2x -1
C.e2x-e-2x +1
D. c1e2x+c2e-2x -2答案：B解析：提示：①求对应齐次方程通解。
-
第2题：
函数y=c1e2x+c2(其中c1、c2是任意常数)是微分方程
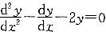
的( )。A.通解
B.特解
C.不是解
D.是解，但不是通解也不是特解答案：D解析：y=c1e2x+c2=c3e2x经验证是方程的解，但不是通解也不是特解 -
第3题：
微分方程y''+2y=0的通解是：
(A,B为任意常数）答案：D解析：提示:本题为二次常系数线性齐次方程求通解，写出方程对应的特征方程r2+2 = 0,r =
-
第4题：
微分方程y''=(y')2的通解是：
A. lnx+c B. ln(x+c)
C. c2+ln x+c1 D. c2-lnlx+c1
(以上各式中，c1、c2为任意常数）答案：D解析：提示:此题为可降阶的高阶微分方程，按方程不显含变量y计算。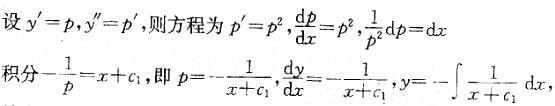
y=c2-lnlx+c1 -
第5题：
微分方程ydx+(x-y)dy=0的通解是:(c为任意常数)
答案：A解析：
-
第6题：
微分方程y''=y'2的通解是（ ）（C1、C2为任意常数）。
答案：D解析：提示：这是不显含y可降阶微分方程，令p=y',则dp/dx=y'',用分离变量法求解得，-y'=1/(x+C1) ，两边积分，可得y=C2-ln x+C1 ，故应选D,也可采用检验的方式。 -
第7题：
微分方程y"=y’2的通解是（）（C1、C2为任意常数）。
- A、lnx+C
- B、ln（x+C）
- C、C2+ln
- D、C2-ln
正确答案:D -
第8题：
单选题函数（C1，C2为任意数）是微分方程y″－y′－2y＝0的（ ）。[2014年真题]A通解
B特解
C不是解
D解，既不是通解又不是特解
正确答案： D解析：
微分方程y″－y′－2y＝0的特征方程为：r2－r－2＝0，解特征方程得：r1＝2，r2＝－1。故其通解为：y＝C1e2x＋C2e－x，即题中函数是方程的解，但不是通解或特解。 -
第9题：
单选题y″－4y＝e2x的通解为（ ）。Ay＝C1e－2x－（C2＋x/4）e－2x（其中C1，C2为任意常数）
By＝C1e－2x＋（C2＋x/4）e2x（其中C1，C2为任意常数）
Cy＝C1e－2x＋（C2＋x/4）e－2x（其中C1，C2为任意常数）
Dy＝C1e－2x－（C2＋x/4）e2x（其中C1，C2为任意常数）
正确答案： D解析：
原方程为y″－4y＝e2x，其齐次方程对应的特征方程为r2－4＝0，解得r1，2＝±2，故其对应的齐次方程y″－4y＝0的通解为y1＝C1e－2x＋C2e2x。因为非齐次方程右端的非齐次项为e2x，2为特征方程的单根，故原方程特解可设为y*＝Axe2x，代入原方程得A＝1/4，故原方程的通解为y＝y1＋y*＝C1e－2x＋C2e2x＋xe2x/4，其中C1，C2为任意常数。 -
第10题：
单选题二阶常系数非齐次线性微分方程y″－4y′＋3y＝2e2x的通解为y＝（ ）。AC1x＋C2x3＋2e2x（其中C1，C2为任意常数）
BC1x＋C2x3－2e2x（其中C1，C2为任意常数）
CC1ex＋C2e3x－2e2x（其中C1，C2为任意常数）
DC1ex＋C2e3x＋2e2x（其中C1，C2为任意常数）
正确答案： A解析：
原微分方程为y″－4y′＋3y＝2e2x，对应齐次方程y″－4y′＋3y＝0的特征方程为r2－4r＋3＝0，特征根为r1＝1，r2＝3。故原方程所对应齐次方程的通解为y＝C1ex＋C2e3x。设y*＝Ae2x是原方程的特解，代入原方程解得A＝－2，故原方程的通解为y＝C1ex＋C2e3x－2e2x，其中C1，C2为任意常数。 -
第11题：
单选题在下列微分方程中，以y＝C1ex＋C2cos2x＋C3sin2x（C1，C2，C3为任意常数）为通解的是（ ）。Ay‴＋y″－4y′－4y＝0
By‴＋y″＋4y′＋4y＝0
Cy‴－y″－4y′＋4y＝0
Dy‴－y″＋4y′－4y＝0
正确答案： B解析：
根据题设中通解的形式可知，所求齐次方程中对应的特征根为r1＝1，r2，3＝±2i。故特征方程为（r－1）（r－2i）（r＋2i）＝0即r3－r2＋4r－4＝0，则所求微分方程为y‴－y″＋4y′－4y＝0。 -
第12题：
微分方程(1+y)dx-(1-x)dy=0的通解是(c为任意常数)：
答案：C解析：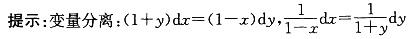
积分得：ln(1-x)+ln(1+y)=lnc。 -
第13题：
微分方程y′′=x+sinx的通解是(C1，C2为任意常数）：
答案：B解析：
-
第14题：
微分方程y′′-4y=4的通解是(C1，C2为任意常数）：A.C1e2x-C2e-2x+1
B. C1e2x+C2e-2x-1
C.e2x-e-2x+1
D. C1e2x+C2e-2x-2答案：B解析：
-
第15题：
微分方程y''-4y=4的通解是(c1，c2为任意常数)：
A. c1e2x-c2e-2x+1B. c1e2x+c2e-2x-1
C. e2x-e-2x+1 D.c1e2x+c2e-2x-2答案：B解析：提示:①求对应齐次方程通解。
r2-4=0，r=±2，通解y=C1e-2x+c2e2x
②把某一数字代入方程检验，得非齐次特解y*=-1。
③非齐次通解=齐次通解+非齐次一个特解。 -
第16题：
微分方程y''=(y')2的通解是：A. lnx+c
B. ln(x+c)
C. c2+ln x+c1
D. c2-lnlx+c1
（以上各式中，c1、c2为任意常数）答案：D解析：提示 此题为可降阶的高阶微分方程，按方程不显含变量y计算。
y=c2-lnlx+c1 。 -
第17题：
二阶常系数齐次微分方程y″-4y′+4y=0的通解为_____．答案：解析：
-
第18题：
单选题微分方程y"=y’2的通解是（）（C1、C2为任意常数）。Alnx+C
Bln（x+C）
CC2+ln
DC2-ln
正确答案： C解析： 暂无解析 -
第19题：
单选题（2008）微分方程y″=（y′）2的通解是：（c1，c2为任意常数）（）Alnx+c
Bln（x+C.
Cc2+ln│x+c1│
Dc2-ln│x+c1│
正确答案： C解析： 暂无解析 -
第20题：
单选题欧拉方程x2d2y/dx2＋4xdy/dx＋2y＝0（x＞0）的通解为（ ）。Ac1/x＋c2/x2（其中c1，c2为任意常数）
Bc1/x2＋c2/x3（其中c1，c2为任意常数）
Cc1/x3＋c2/x4（其中c1，c2为任意常数）
Dc1/x4＋c2/x5（其中c1，c2为任意常数）
正确答案： B解析：
原方程为x2d2y/dx2＋4xdy/dx＋2y＝0。令x＝et，则原方程可化为D（D－1）y＋4Dy＋2y＝0，即d2y/dt2＋3dy/dt＋2y＝0。其相应的特征方程为r2＋3r＋2＝（r＋1）（r＋2）＝0，解得r1＝－1，r2＝－2。故变形后的方程得通解为Y＝c1e－t＋c2e－2t，则原方程的通解为Y＝c1/x＋c2/x2其中c1，c2为任意常数。 -
第21题：
填空题设y＝ex（c1sinx＋c2cosx）（c1、c2为任意常数）为某二阶常系数线性齐次微分方程的通解，则该方程为____。正确答案： y″-2y′+2y=0解析：
根据题中所给的通解y＝ex（c1sinx＋c2cosx）的结构可知，所求方程对应的特征根为λ1，2＝1±i，特征方程为[λ－（1＋i）][λ－（1－i）]＝λ2－2λ＋2＝0，则所求方程为y″－2y′＋2y＝0。 -
第22题：
单选题欧拉方程x2d2y/dx2＋4xdy/dx＋2y＝0（x＞0）的通解为（ ）。Ac1/x－c2/x3（其中c1，c2为任意常数）
Bc1/x＋c2/x2（其中c1，c2为任意常数）
Cc1/x＋c2/x3（其中c1，c2为任意常数）
Dc1/x－c2/x2（其中c1，c2为任意常数）
正确答案： C解析：
原方程为x2d2y/dx2＋4xdy/dx＋2y＝0。令x＝et，则原方程可化为D（D－1）y＋4Dy＋2y＝0，即d2y/dt2＋3dy/dt＋2y＝0。其相应的特征方程为r2＋3r＋2＝（r＋1）（r＋2）＝0，解得r1＝－1，r2＝－2。故变形后的方程得通解为Y＝c1e－t＋c2e－2t，则原方程的通解为Y＝c1/x＋c2/x2其中c1，c2为任意常数。