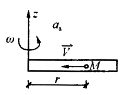
水平管以角速度w绕铅垂轴Z转动。管内有一小球M以速度V=rw沿管运动,r为小球到转轴的距离。球M的绝对速度是( )。
题目
水平管以角速度w绕铅垂轴Z转动。管内有一小球M以速度V=rw沿管运动,r为小球到转轴的距离。球M的绝对速度是( )。
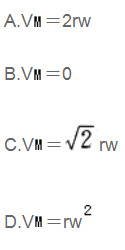

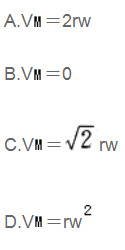
相似考题
更多“水平管以角速度w绕铅垂轴Z转动。管内有一小球M以速度V=rw沿管运动,r为小球到转轴的距离。球M的绝对速度是( )。 ”相关问题
-
第1题:
细管OB以角速度ω,角加速度α绕O轴转动,一小球A在管内以相对速度
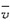
由O向B运动,动坐标同结于OB管上。图示瞬时,小球A的牵连加速度为( )。
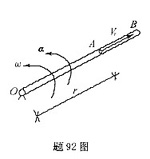
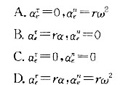
答案:A解析:对小球而言牵连运动指管绕O轴的转动 -
第2题:
图示均质圆轮,质量为m,半径为r,在铅垂图面内绕通过圆盘中心O的水平轴转动,角速度为ω,角加速度为ε,此时将圆轮的惯性力系向O点简化,其惯性力主矢和惯性力主矩的大小分别为( )。
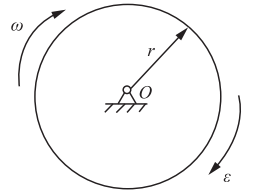
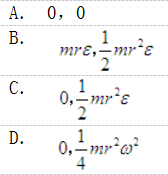 答案:C解析:
答案:C解析: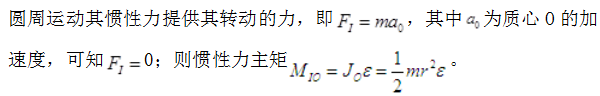
-
第3题:
均质圆盘质量为m,半径为R,在铅垂面绕内O轴转动,图示瞬间角速度为ω,则其对O轴的动量矩大小为( )。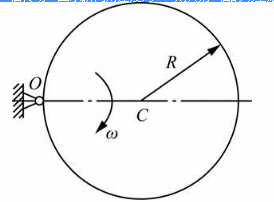 A.mRω
A.mRω
B.mRω/2
C.mR2ω/2
D.3mR2ω/2答案:D解析:根据质点的动量矩公式,体系对O点的动量矩为: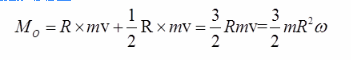
-
第4题:
忽略质量的细杆OC=l,其端部固结匀质圆盘圆心,盘质量为m,半径为r。系统以角速度w绕轴O转动。系统的动能是: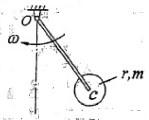
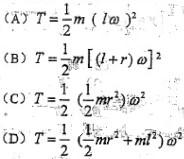 答案:D解析:此为定轴转动刚体,动能表达式为
答案:D解析:此为定轴转动刚体,动能表达式为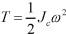 ,其中Jc为刚体通过质心且垂直于运动平面
,其中Jc为刚体通过质心且垂直于运动平面
的轴的转动惯量。
此题中,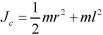 ,带入动能表达式,选(D)。
,带入动能表达式,选(D)。 -
第5题:
如图所示圆环以角速度ω绕铅直轴AC自由转动,圆环的半径为R,对转轴的转动惯量为I;在圆环中的A点放一质量为m的小球,设由于微小的干扰,小球离开A点。忽略一切摩擦,则当小球达到B点时,圆环的角速度是( )。

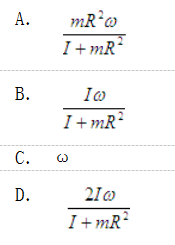 答案:B解析:
答案:B解析:
-
第6题:
如图所示质量为m、长为l的均质杆OA绕O轴在铅垂平面内作定轴转动。已知某瞬时杆的角速度为ω,角加速度为α,则杆惯性力系合力的大小为( )。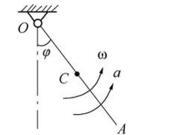
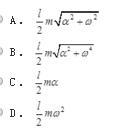 答案:B解析:
答案:B解析:
-
第7题:
忽略质量的细杆OC=l,其端部固结匀质圆盘。杆上点C为圆盘圆心。盘质量为m,半径为r。系统以角速度ω绕轴O转动。系统的动能是: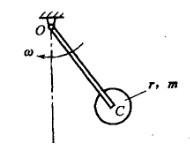
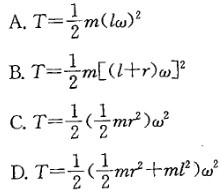 答案:D解析:提示:圆盘绕轴O作定轴转动,其动能为T=1/2JOω2。
答案:D解析:提示:圆盘绕轴O作定轴转动,其动能为T=1/2JOω2。 -
第8题:
图示均质圆轮,质量为m,半径为r,在铅垂图面内绕通过圆盘中心O的水平轴转动,角速度为w,角加速度为ε,此时将圆轮的惯性力系向O点简化,其惯性力主矢和惯性力主矩的大小分别为: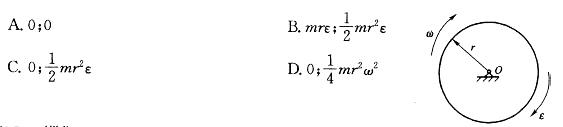 答案:C解析:根据 定轴转动刚体惯性力系的简化结果,惯性力主矢和主矩的大小分别为F1=mac,MIO=JOa。
答案:C解析:根据 定轴转动刚体惯性力系的简化结果,惯性力主矢和主矩的大小分别为F1=mac,MIO=JOa。 -
第9题:
图4-67示均质圆轮,质量为m,半径为r,在铅垂图面内绕通过圆轮中心O的水平轴以匀角速度ω转动。则系统动量、对中心O的动量矩、动能的大小为( )。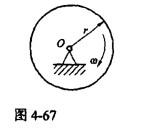
 答案:A解析:提示:根据动量、动量矩、动能的定义,刚体作定轴转动时,ρ = mvc、LO= JOω, T=1/2JOω2。
答案:A解析:提示:根据动量、动量矩、动能的定义,刚体作定轴转动时,ρ = mvc、LO= JOω, T=1/2JOω2。 -
第10题:
刚体以角速度ω,角加速度ε绕定轴转动则在其转动半径为r处的线速度v=(),切线加速度at=(),法向加速度an=()。
正确答案:ωr;εr;ω2r -
第11题:
一质量为M,半径为R的飞轮绕中心轴以角速度ω作匀速转动,其边缘一质量为m的碎片突然飞出,则此时飞轮的()。
- A、角速度减小,角动量不变,转动动能减小
- B、角速度增加,角动量增加,转动动能减小
- C、角速度减小,角动量减小,转动动能不变
- D、角速度不变,角动量减小,转动动能减小
正确答案:D -
第12题:
均质圆盘质量为m,半径为R,在铅垂平面内绕O轴转动,图示瞬时角速度为ω,则其对O轴的动量矩和动能大小分别为: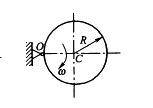
 答案:D解析:
答案:D解析:
-
第13题:
图示质量为m、长为l的杆OA以的角速度绕轴O转动,则其动量为: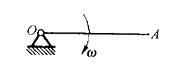
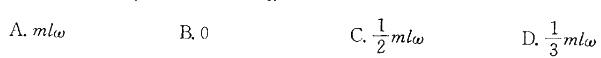 答案:C解析:提示:根据动量的公式:p=mvc。
答案:C解析:提示:根据动量的公式:p=mvc。 -
第14题:
忽略质量的细杆OC=l,其端部固结匀质圆盘。杆上点C为圆盘圆心。盘质量为m,半径为r。系统以角速度ω绕轴O转动,如图所示。系统的动能是: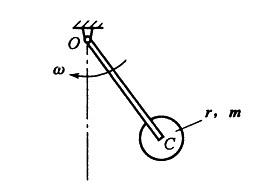
 答案:D解析:
答案:D解析:
-
第15题:
均质圆盘质量为m,半径为R,再铅垂面内绕o轴转动,图示瞬吋角速度为w,则其对o轴的动量矩和动能的大小为: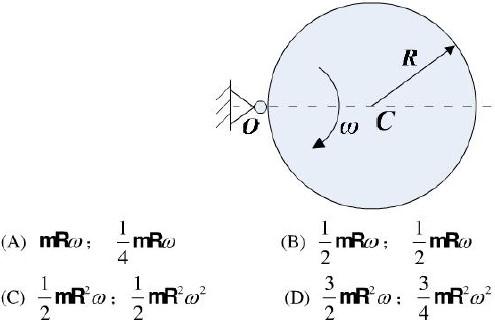 答案:C解析:解:选C
答案:C解析:解:选C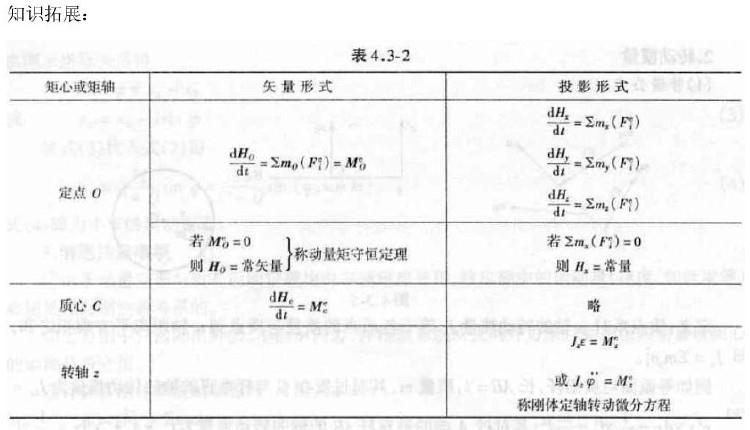

-
第16题:
图示均质圆轮,质量为m,半径为r,在铅垂图面内绕通过圆轮中心O的水平轴以匀角速度ω转动。则系统动量、对中心O的动量矩、动能的大小为: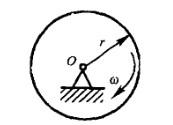
 答案:A解析:提示:根据动量、动量矩、动能的定义,刚体做定轴转动时p=mvc, LO=JOω,T=1/2JOω2。
答案:A解析:提示:根据动量、动量矩、动能的定义,刚体做定轴转动时p=mvc, LO=JOω,T=1/2JOω2。 -
第17题:
均质细直杆OA长为l ,质量为m,A端固结一质置为m的小球(不计尺寸),如图所示。当OA杆以匀角速度w绕O轴转动时,该系统时O轴的动量矩为: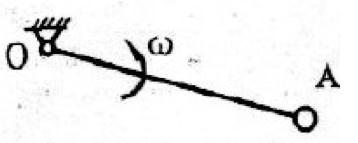
 答案:D解析:
答案:D解析:
-
第18题:
图示曲柄连杆机构中,OA=r,AB=2r,OA、AB及滑块B质量均为m,曲柄以ω的角速度绕O轴转动,则此时系统的动能为:
 答案:A解析:提示:杆AB瞬时平移,杆OA做定轴转动,滑块B为质点,分别根据动能的定义求解。
答案:A解析:提示:杆AB瞬时平移,杆OA做定轴转动,滑块B为质点,分别根据动能的定义求解。 -
第19题:
如图4-48所示直角弯杆OAB以匀角速度ω绕O轴转动,并带动小环M沿OD杆运动。已知OA=l,取小环M为动点,OAB杆为动系,当 φ =60°时,M点牵连加速度ae的大小为( )。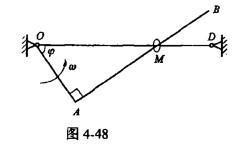
 答案:D解析:
答案:D解析: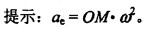
-
第20题:
如图4-57所示质量为m、长为l 的杆OA以ω的角速度绕轴O转动,则其动量为 ( )。
 答案:C解析:提示:根据动量的公式ρ =mvc。
答案:C解析:提示:根据动量的公式ρ =mvc。 -
第21题:
一飞轮以角速度ω0绕光滑固定轴旋转,飞轮对轴的转动惯量为J1;另一静止飞轮突然和上述转动的飞轮啮合,绕同一转轴转动,该飞轮对轴的转动惯量为前者的二倍,啮合后整个系统的角速度ω=()。
正确答案:(1/3)ω0 -
第22题:
单选题质量为2m,半径为R的偏心圆板可绕通过中心O的轴转动,偏心距OC= 。在OC连线上的A点固结一质量为m的质点,OA=R如图示。当板以角速度w绕轴O转动时,系统动量K的大小为()。(注:C为圆板的质心)。AK=0
BK=mRw
CK=mRw
DK=2mRw
正确答案: A解析: 暂无解析
