均质杆AB长为l，重为W，受到如图所示的约束，绳索ED处于铅垂位置，A、B两处为光滑接触，杆的倾角为α，又CD = l/4，则 A、B两处对杆作用的约束力大小关系为：A. FNA=FNB= 0 B. FNA=FNB≠0 C. FNA≤FNB D.FNA≥FNB

题目
均质杆AB长为l，重为W，受到如图所示的约束，绳索ED处于铅垂位置，A、B两处为光滑接触，杆的倾角为α，又CD = l/4，则 A、B两处对杆作用的约束力大小关系为：

A. FNA=FNB= 0 B. FNA=FNB≠0 C. FNA≤FNB D.FNA≥FNB

相似考题

1.质量为m，长为2l的均质杆初始位于水平位置， 如图所示。A端脱落后，杆绕轴B转动，当杆转到铅垂位置时，AB 杆B处的约束力大小为：

2.质量为m，长为2l的均质细杆初始位于水平位置，如图所示。A端脱落后，杆绕轴B转动，当杆转到铅垂位置时，AB杆角加速度的大小为：

3.已知杆AB和杆CD的自重不计，且在C处光滑接触，若作用在杆AB上力偶矩为M1，若欲使系统保持平衡，作用在CD杆上力偶矩M2的，转向如图所示，则其矩值为：

4.均质细直杆AB长为l，质量为m，以匀角速度ω绕O轴转动，如图所示，则AB杆的动能为：

参考答案和解析
答案：B
解析：
提示:A、B处为光滑约束，其约束力均为水平并组成一力偶，与力W和DE杆约束力组成的力偶平衡。
更多“均质杆AB长为l，重为W，受到如图所示的约束，绳索ED处于铅垂位置，A、B两处为光滑接触，杆的倾角为α，又CD = l/4，则 A、B两处对杆作用的约束力大小关系为： ”相关问题

  • 第1题：

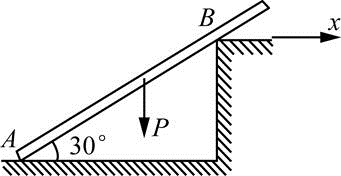
    杆AB的A端置于光滑水平面上，AB与水平面夹角为 30°，杆重为P，如图所示，B处有摩擦，则杆AB平衡时，B处的摩擦力与x方向的夹角为（　　）。




    A、90°
    B、30°
    C、60°
    D、45°

    答案：B
    解析：
    分析AB杆受力，易得AB杆受力图如题50解图所示，即有B处的摩擦力与x方向的夹角30°。


  • 第2题：

    匀质杆质量为m，长OA=l，在铅垂面内绕定轴o转动。杆质心C处连接刚度系数是较大的弹簧，弹簧另端固定。图示位置为弹簧原长，当杆由此位置逆时针方向转动时，杆上A点的速度为VA，若杆落至水平位置的角速度为零，则vA的大小应为：


    答案：D
    解析：

  • 第3题：

    如图所示，结构由AB、BC、CE三杆铰接而成，A处为固定端，杆重不计，铰C上作用一铅垂力P，则二力杆为（　　）。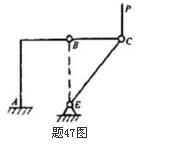

    A．AB、BC、CE
    B．BC、CE
    C．AB
    D．均不是二力杆

    答案：B
    解析：
    在铅垂力P的作用下，此结构处于平衡状态。由二力平衡原理，不计自重的刚体在二力作用下平衡的必要充分条件是：二力沿着同一作用线、大小相等、方向相反。仅受两个力作用且处于平衡状态的物体，称为二力体，又称二力杆件，故杆BC和杆CE是二力杆。

  • 第4题：

    已知杆AB和杆CD的自重不计，且在C处光滑接触，若作用在杆AB上的力偶的矩为m1，则欲使系统保持平衡，作用在CD杆上的力偶矩m2，转向如图所示，其矩的大小为：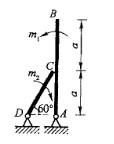



    答案：A
    解析：
    提示:根据受力分析，A、C、D处的约束力均为水平方向，分别考虑杆AB、DC的平衡，采用力偶的平衡方程即可。

  • 第5题：

    杆AB长为l，质量为m，图示瞬时点A处的速度为v，则杆AB的动量大小为: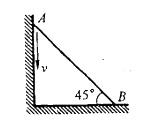



    答案：D
    解析：
    提示：动量的大小等于杆AB的质量乘以其质心速度的大小。

  • 第6题：

    质量为m,长为2l的均质细杆初始位于水平位置，如图所示。A端脱落后，杆绕轴B 转动，当杆转到铅通位置时，AB杆角加速度的大小为：


    答案：C
    解析：
    解：选C
    报据机械能守恒定律，在等式两边对初始和最终时刻的两祌情形列出动能和势能，再求解即可得到答案。

  • 第7题：

    T形均质杆OABC以匀角速度ω绕O轴转动，如图所示。已知OA杆的质量为2m，长为2l，BC杆质量为m，长为l，则T形杆在图示位置时动量的大小为：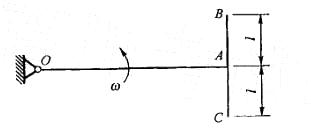



    答案：C
    解析：
    提示：动量 p=∑mivci=(2m?lω+m?2lω)j。

  • 第8题：

    质量为m，长为2l的均质细杆初始位于水平位置，如图4-68所示。A端脱落后， 杆绕轴B转动，当杆转到铅垂位置时，AB杆B处的约束力大小为（ ）。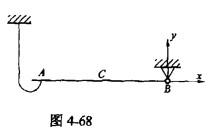



    答案：D
    解析：
    提示：根据动能定理，当杆转动到铅垂位置时，杆的ω2=3g/2l，α=0，根据质心运动定理mlω2=FBy－mg，FBx=0。

  • 第9题：

    图4-22中，均质杆AB重力为F,用铅垂绳CD吊在天花板上，A、B两端分别靠在光滑的铅垂墙面上，则A、B两端约束力的大小是( )。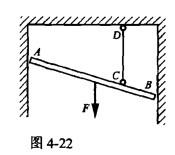

    A. A、B两点约束力相等 B. B点约束力大于A点约束力
    C. A点约束力大于B点约束力 D.无法判断


    答案：A
    解析：
    提示：A、B处为光滑约束，其约束力均为水平并组成一力偶，与力F和CD杆约束力组成的力偶平衡。

  • 第10题：

    杆AB长为l,质量为m，图4-64所示瞬时点A处的速度为V,则杆动量的大小为（ ）。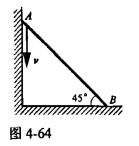



    答案：D
    解析：
    提示：动量的大小等于杆AB的质量乘以其质心速度的大小。

  • 第11题：

    T形均质杆OABC以匀角速度ω绕O轴转动，如图所示。已知OA杆的质量为2m，长为2l，BC杆质量为m，长为l，则T形杆在该位置对O轴的动量矩为：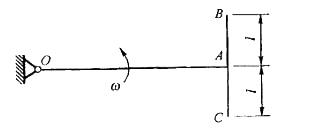




    答案：C
    解析：
    提示：动量矩 LO=JOω，其中JO=JO(OA)+ JO(BC)。

  • 第12题：

    均质细杆AB重力为P、长2L，A端铰支，B端用绳系住，处于水平位置，如图所示，当B端绳突然剪断瞬时，AB杆的角加速度大小为：



    答案：B
    解析：

  • 第13题：

    均质细杆重力为P、长2L，A端铰支，B端用绳系住，处于水平位置，如图所示。当B端绳突然剪断瞬时，AB杆的角加速度大小为：



    答案：B
    解析：
    提示:可用动静法，将惯性力向A点简化。

  • 第14题：

    图示均质细直杆AB长为l，质量为m，图示瞬时A点的速度为则AB杆的动量大小为：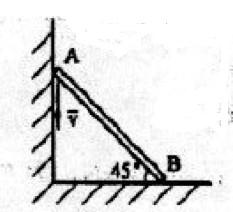



    答案：D
    解析：
    质点系动量：，为各质点动量的矢量和，图示杆的质心在杆中端。

  • 第15题：

    均质细杆AB重力为P，长为2l，A端铰支，B端用绳系住，处于水平位置，如图所示。当B端绳突然剪断瞬时，AB杆的角加速度大小为3g/4l，则A处约束力大小为：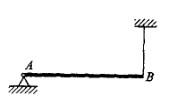

    A. FAx= 0,FAy=0 B. FAx= 0,FAy=P/4 C. FAx= P,FAy=P/2 D.FAx= 0,FAy=P


    答案：B
    解析：

  • 第16题：

    如图所示质量为m、长为l的均质杆OA绕O轴在铅垂平面内作定轴转动。已知某瞬时杆的角速度为ω，角加速度为α，则杆惯性力系合力的大小为（　　）。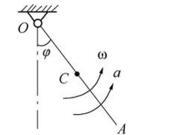


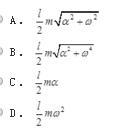    答案：B
    解析：

  • 第17题：

    均质细直杆长为l，质量为m，图示瞬时点A处的速度为v，则杆AB的动量大小为：


    答案：D
    解析：
    提示 动量的大小等于杆AB的质量乘以其质心速度的大小。

  • 第18题：

    已知杆AB和杆CD的自重不计，且在C处光滑接触，若作用在杆上的力偶的矩为m1,则欲使系统保持平衡，作用在CD杆上的力偶矩m2，转向如图4-14所示，其矩的大小为（ ）。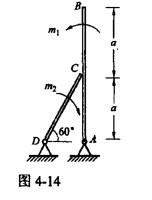



    答案：A
    解析：
    提示：作用在AB杆C处的约束力为水平方向，根据力偶的性质，A、D处约束力应满足二力平衡原理。

  • 第19题：

    均质细直杆AB长为l，质量为m,以匀角速度ω绕O轴转动，如图4-69所示， 则AB杆的动能为（ ）。



    答案：D
    解析：
    提示：定轴转动刚体的动能为T = 1/2JOω2。

  • 第20题：

    均质杆长为l，其B端放在水平光滑面上，杆与地面成θ角时无初速地自由倒下，则质心C（）。

    • A、质点动量没有改变
    • B、质点动量的改变量大小为2mv，方向铅垂向上
    • C、质点动量的改变量大小为2mv，方向铅垂向下
    • D、质点动量的改变量大小为mv，方向铅垂向下

    正确答案:C

相关内容