长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为（）A.8π B.10π C.12π D.14π E.16π

题目

长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为（）

A.8π
B.10π
C.12π
D.14π
E.16π

相似考题

1.图的遍历要求从图的某一顶点出发,访遍图中的其余顶点,且每个顶点仅被访问一次。()此题为判断题(对，错)。

2.用构成物体的各顶点坐标和连接各顶点所形成的边来描述物体的造型方法称为()A、线框造型B、曲面造型C、表面造型D、实体造型

3.一个正八面体两个相对的顶点分别为A和B，一个点从A出发，沿八面体的棱移动到B位置，其中任何顶点最多到达1次，且全程必须走过所有8个面的至少1条边，问有多少种不同的走法？（）A．8 B．16 C．24 D．32

4.图的遍历是从图中的某个顶点出发,按照某种搜索策略访问图中所有顶点且每个顶点仅访问一次。()此题为判断题(对，错)。

更多“长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为（）”相关问题

第1题：

一个长7厘米、宽5厘米、高3厘米的长方体盒子。一只瓢虫从盒子的任意一个顶点，爬到与设定点在同一体对角线的另一个顶点，则所有情形的爬行路线的最小值是()。
A. B. C. D.

正确答案：D
把纸盒由立体展为平面，则飘虫从一个顶点走向同一体对角线的最短距离为。故本题正确答案为D。
第2题：

一个长方体的所有棱长之和是72 cm，它的长宽高之比是3：2：1，则长方体体积为( )。

A.162 cm3
B.1296 cm3
C.2592 cm3
D.10368 cm3

答案：A
解析：
由长方体性质知，长方体长、宽、高之和为72÷4=18 cm，则可得出长为9 cm，宽为6 cm，高为30m．所以体积为9×6×3=162 cm3。
第3题：

一个正方体的边长为1，一只蚂蚁从其一个角出发，沿着正方体的棱形进，直到经过该正方体的每一条棱为止（经过一个顶点即算作经过该顶点所连接的3条棱）。则其最短的行进距离为（）。

A. 3
B. 4
C. 5
D. 6

答案：C
解析：
蚂蚁行进路径如下图2所示，故本题答案为C选项。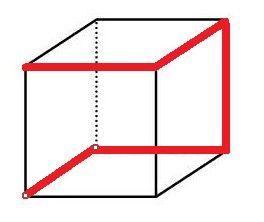
第4题：

如图为长、宽、高分别是4cm、3cm、5cm的长方体，如果一只小虫从顶点A爬到顶点B，其爬行的最短距离为( )cm 。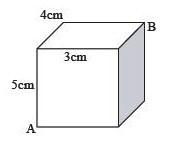

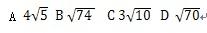答案：B
解析：
第5题：

一个正八面体两个相对的顶点分别为A和B，一个点从A出发，沿八面体的棱移动到B位置，其中任何顶点最多到达1次，且全程必须走过所有8个面的至少1条边，问有多少种不同的走法？（）
A．8 B．16 C．24 D．32

答案：A
解析：
本题属于几何问题。在如图所示的正八面体中，假设从最上面的A点出发，要达到最下面的B点，首先要经过中间平面上的四个点，此时4条路线是对称的。假设从A先到点1，下一步有点2和点4两种选择，此时已经有4×2=8种路线。但从点2走到点3之后，不能直接到B点，必须再经过点4，否则不满足“走过所有8个面的至少1条边”，因此总的走法就是8种。所以选择A选项。
第6题：

若正三棱锥底面边长为a，且三条侧棱两两垂直，则它的体积为_____．

答案：
解析：
第7题：

正三棱柱的每条棱长都是a，则经过底面一边和相对顶点的截面面积是（）

答案：B
解析：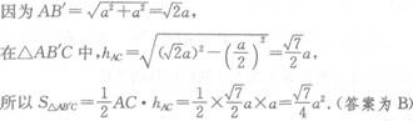
第8题：

下图是一个软件项目的活动图，其中顶点表示项目里程碑，连接顶点的边表示包含的活动，则里程碑（请作答此空）在关键路径上。活动GH的松弛时间是（）。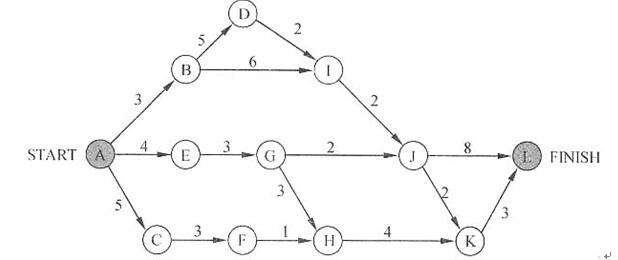

A.B
B.E
C.C
D.K

答案：A
解析：
本题考查活动图的基础知识。
根据关键路径法，计算出关键路径为A-B-D-I-J-L，其长度为20。因此里程碑B在关键路径上，而里程碑E、C和K不在关键路径上。包含活动GH的最长路径是A-E-G-H-K-L，长度为17，因此该活动的松弛时间为20-17=3。
第9题：

球头铣刀刀位点是球顶点。

正确答案:错误
第10题：

反手握拍时拇指顶点在拍柄内侧的宽面上或（）上
- A、外侧棱
- B、内侧棱
- C、外侧的宽面
- D、内侧的宽面
正确答案:B
第11题：

填空题
长方体同一顶点处三条棱长的和是a，它的一条对角线长是b，这个长方体的全面积是____．

正确答案： (a+b)(a-b)
解析：
设长方体三条棱长分别为x，y，z，则有x＋y＋z＝a，即（x＋y＋z）²＝x²＋y²＋z²＋2xy＋2yz＋2xz＝a²．
又因x²＋y²＋z²＝b²，代入上式得2（xy＋yz＋xz）＝a²－b²＝（a＋b）（a－b）．
第12题：

单选题
反手握拍时拇指顶点在拍柄内侧的宽面上或（）上
A
外侧棱
B
内侧棱
C
外侧的宽面
D
内侧的宽面

正确答案： B
解析：暂无解析
第13题：

有白球和黑球各3个且白球和黑球中各有两个球分别印有1、2两个号码。现将这6个球放入袋子里，充分搅匀后有放回地每次摸取一个球，则前两次恰好摸到同编号的异色球的概率为（）。

答案：D
解析：
第一次取到有编号的球的概率为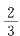，假设取到白色1号球，则第二次必须取到黑色1号球，其概率为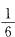。因此前两次恰好摸到同编号的异色球的概率为。。
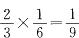第14题：

同一球面上四点A，B，C，D满足AB=BC=√2，AC=2，且球的表面积为(25/4)π，则四面体ABCD体积的最大值为________。

答案：
解析：
第15题：

一个长方体零件的长、宽和高分别为X+4、X+2、和X厘米，其所有棱长之和为168厘米，则该长方体零件的体积为多少立方厘米？《》（）

A.1680
B.2184
C.2688
D.2744

答案：C
解析：
第16题：

一个长7厘米、宽5厘米、高3厘米的长方体盒子。一只瓢虫从盒子的任意一个顶点，爬到与设定点在同一体对角线的另一个顶点，则所有情形的爬行路线的最小值是()。

A. √ 153
B. √ 109
C. √ 171
D. √ 113

答案：D
解析：
把纸盒由立体展为平面，则飘虫从一个顶点走向同一体对角线的最短距离为√ 下7的平方加上（3+5）的平方。故答案为D。
第17题：

三个相同的盒子里各有2个球，其中一个盒子里放了2个红球，一个盒子里放了2个蓝球，一个盒子里放了红球和蓝球各1个。随机选择一个盒子后从中随机摸出一球是红球，则这个盒子里另一个球是红球的概率为（）。

A.1/2
B.3/4
C.2/3
D.4/5

答案：C
解析：
第18题：

棱长等于1的正方体内接于一球体中，则该球的表面积是（　　）

A.3π
B.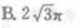
C.6π
D.9π

答案：A
解析：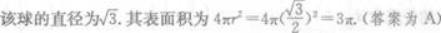
第19题：

棱长为3的正四面体，以其3个侧面的重心为顶点的三角形面积为：

答案：A
解析：
正四面伴的侧面是等边三角形，其重心为各边中线的交点。如左图可知，重心O将中线
第20题：

有关球性软性角膜接触镜度数的确定，说法错误的是（）。
- A、只换算验光处方的球镜度数，散光度数可以忽略不计
- B、超过-4.00D需要顶点焦度换算
- C、根据验光处方的等效球镜量进行顶点焦度换算
- D、不需要进行戴镜验光
正确答案:A
第21题：

语句drawRect（40，50，160，150）执行的结果是（）。
- A、画一个左上角顶点是（40，50）、右下角顶点是（160，150）的矩形
- B、画一个左上角顶点是（40，50）、宽160，长150的矩形
- C、画一个右上角顶点是（40，50）、左下角顶点是（160，150）的矩形
- D、画一个右上角顶点是（40，50）、宽160，长150的矩形
正确答案:B
第22题：

正面上手传球时，其击球点应在脸额前上方约（）距离处。
- A、一球
- B、二球
- C、三球
- D、三球
正确答案:A
第23题：

单选题
长方体同一顶点处三条棱长的和是a，它的一条对角线长是b，这个长方体的全面积是（　　）．
A
（a＋b）（a－b）
B
（a＋b）²
C
（a－b）²
D
a²－ab＋b²

正确答案： B
解析：
设长方体三条棱长分别为x，y，z，则有x＋y＋z＝a，即（x＋y＋z）²＝x²＋y²＋z²＋2xy＋2yz＋2xz＝a²．又因x²＋y²＋z²＝b²，代入上式得2（xy＋yz＋xz）＝a²－b²＝（a＋b）（a－b）．

长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为（ ）A.8π B.10π C.12π D.14π E.16π

题目

相似考题

更多“长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为（ ）”相关问题

相关内容

长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为（）A.8π B.10π C.12π D.14π E.16π

更多“长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为（）”相关问题